图无处不在

解决 “ZigZag 转换”问题 的传统方法是构建一个二维表格或找到同一行字母索引之间的模式。 还有一种基于 BFS（广度优先搜索）的美妙解决方案。

问题

字符串 "PAYPALISHIRING" 按照如下方式在给定的行数上以之字形模式书写：（你可能希望以固定字体显示此模式以获得更好的可读性）

P   A   H   N
A P L S I I G
Y   I   R

然后按行读取："PAHNAPLSIIGYIR"

编写代码，将接受一个字符串并进行此转换，给定行数

string convert(string text, int nRows);

convert("PAYPALISHIRING", 3) 应该返回 "PAHNAPLSIIGYIR"。

广度优先搜索

将字符串中的每个字母视为图中的一个节点。 如果我们按照原始字符串的顺序链接节点，实际上就是构建一个图。 每个节点最多可以有两个邻居。 原始字符串中字母的顺序实际上是对此图进行 DFS（深度优先搜索）的结果。

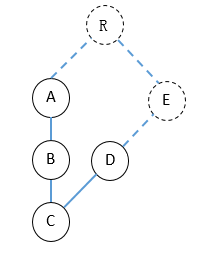
例如，对于字符串“ABCDE”，

A   E
B D
C

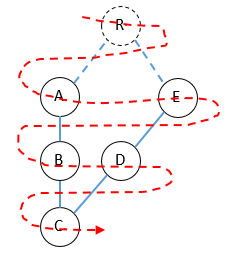
生成的图如下。 我们在第一行的节点和根之间创建一些虚拟路径。

BFS 遍历产生“AEBDC”，这正是我们想要的。

只剩下一件事了。 如果节点“E”不存在怎么办？ 对于最后一个分支（例如，这里是 C->D），我们可能需要创建一个虚拟路径来连接到根，如下所示。

代码如下。

from collections import deque

class Node:
    def __init__(self, value):
        self.visited = False
        self.value = value
        self.neighbors = []

class Solution:
    # @param {string} s
    # @param {integer} numRows
    # @return {string}
    def convert(self, s, numRows):
        self.__s = s
        self.__numRows = numRows
        return self.__BFS(self.__buildGraph())

    def __connect(self, prev, this):
        prev.neighbors.append(this)
        this.neighbors.append(prev)

    def __buildGraph(self):
       '''Build the graph from DFS traversal of the string'''
       root = Node('')
       prev = None
       row = 0
       up = True
       for i in range(len(self.__s)):
           this = Node(self.__s[i])
           if prev is not None:
               self.__connect(prev, this)
           prev = this
           # Connect nearest nodes(those on row #0) to the root
           if row == 0:
               self.__connect(root, this)

           if up:
               if row < self.__numRows - 1:
                   row += 1
               elif row > 0:
                   row -= 1
                   up = False
           else:
               if row > 0:
                   row -= 1
               elif row < self.__numRows - 1:
                   row += 1
                   up = True

       # The triky part, for BFS later
       # Build a virtual path to connect to the root for the last branch, if not already
       if not up and row < self.__numRows - 2:
           for i in range(row, -1, -1):
               this = Node('')
               self.__connect(prev, this)
               prev = this
           self.__connect(prev, root)

       return root

 def __BFS(self, root):
     '''Breadth First Search gives the desired string'''
     work_queue = deque()
     root.visited = True
     work_queue.append(root)

     s = ''
     while work_queue:
         node = work_queue.popleft()
         # No special action for the root as it is an empty string;)
         s += node.value
         for i in node.neighbors:
             if not i.visited:
             i.visited = True
             work_queue.append(i)
     return s