C++ 实现的快速排序方法，用于对具有大量重复项的数组进行排序。

Mikhail Semenov

4.83/5 (31投票s)

2015 年 8 月 31 日

CPOL

16分钟阅读

56678

459

高效的快速排序方法，用于对具有大量重复元素的数组进行排序。

下载 QuickSortTests3.zip

引言

本文介绍了最适合对含有大量重复元素的数组进行排序的快速排序方法的实现。文中提供了递归实现、使用栈的实现以及多线程实现。其中包括了在4核和2核处理器上的基准测试。还与其它排序方法（Timsort、Heapsort 和 Mergesort）进行了比较。所附代码已使用 VC++ 2015 和 GCC C++ 5.1 测试通过。

背景

自从 Tony Hoare 发表了他的文章《快速排序》[1-3] 以来，已经提出了相当多各种不同的快速排序分区算法。其中一些不太适合对含有重复元素的数组进行排序。例如，当有大量重复元素时，Lomuto 分区法 [4] 很容易耗尽栈空间。在本文中，我将探讨最适合、最高效的用于排序含有重复元素数组的算法。

对含有大量重复元素的数组进行排序的任务看似人为且理论化，但这类任务在现实世界中也能找到：例如，对文本中的单词进行排序。我将展示这个例子。在实践中，当我们使用非唯一键对数据进行排序时，可能会遇到许多类似的问题：电话通话（电话号码是键）、汽车服务（汽车品牌是键）、博物馆访客（访客来源地是键）。

各种分区方案

我选择了以下三种分区方案：Hoare 分区、三路分区和双轴分区。在准备本文期间，我研究了其他方法（Lomuto 分区、Dijkstra 三路分区 [5] 及其修改版）。但它们比所选方法需要更多的比较操作。

Hoare 分区

在通用排序方面，这种分区方法仍然是最高效的方法之一。下面是其在 C++ 中的递归实现

typedef std::ptrdiff_t Index;

template <class Iterator, class Comparison = std::less<>>
void HoareQuickSort(Iterator a, Iterator finish, Comparison compare = Comparison())
{
    Index right = (finish - a) - 1;
    Index left = 0;

    if (right <= left)
        return;

    auto pivot = a[left + (right - left) / 2];

    Index i = left;
    Index j = right;

    while (i <= j)
    {
        while (compare(a[i], pivot))
            ++i;

        while (compare(pivot, a[j]))
            --j;

        if (i <= j)
        {
            std::swap(a[i++], a[j--]);
        }
    }

    HoareQuickSort(a, a + (j + 1), compare);
    HoareQuickSort(a + i, finish, compare);
}

我将在整篇文章中使用 Index 类型。你可能希望将其定义为 int，但不要使用 unsigned 或 std::size_t，因为有些方法需要负值。

Comparison 可以作为函数或比较类来提交。如果未提供比较对象，数组将按升序排序。下面是一些例子

bool gt(double x, double y)
{
    return x > y;
}

struct GT
{
    bool operator()(double x, double y) const
    {
        return x > y;
    }
};

int main()
{
    std::vector<double> a{ -5, 2, 3, 4.5 };
    HoareQuickSort(std::begin(a), std::end(a));
    for (auto&& e : a)
    {
        std::cout << e << " "; // -5 2 3 4.5
    }
    std::cout << std::endl;         

    std::vector<double> x{ -5, 2, 3, 4.5 };
    HoareQuickSort(std::begin(x), std::end(x), gt);
   
    for (auto&& e : x)
    {
        std::cout << e << " "; // 4.5 3 2 -5
    }
    std::cout << std::endl;

    std::vector<double> y{ -15, 20, 3, 4.5 };
    HoareQuickSort(std::begin(y), std::end(y), GT());   

    for (auto&& e : y)
    {
        std::cout << e << " "; // 20 4.5 3 -15
    }
    std::cout << std::endl;
}

三路分区

我将要在这里讨论的分区方案是 Bentley-McIlroy 分区 [6, 7] 的一个轻微修改版，该版本由 Robert Sedgewick [8-10] 修改。这里提出的方法比原始方法的交换次数更少。此分区方案的目标是产生三个分区

“小于”基准值的元素（严格来说，即比较对象返回 true 的元素）；
等于基准值的元素 (!compare(a[i], pivot) && !compare(pivot,a[i]) 为 true)；
“大于”基准值的元素（即比较函数返回 false 的元素）。

但是有多种方法可以实现这一点。在 Bentley-McIlroy 算法中，开头与 Hoare 分区相似：两个索引同时从数组的两端移动。但与此同时，会进行额外的比较，并从等于基准值的元素中创建额外的分区。首先创建四个分区

一些等于基准值的元素；
“小于”基准值的元素；
“大于”基准值的元素；
其余等于基准值的元素。

然后将分区1和4移动到分区2和3之间。你可能会认为这里有很多交换操作，并且可能有更快的方式来实现三路分区。但它似乎是最快的方式。例如，Dijkstra 三路分区 [5] 看起来更简单，但需要更多的比较操作。

下面是三路快速排序在 C++ 中的递归实现

template <class Iterator, class Comparison = std::less<>>
void ThreeWayQuickSort(Iterator a, Iterator finish, Comparison compare = Comparison())
{
    Index right = (finish - a) - 1;
    Index left = 0;

    if (right <= 0)
        return;

    Index idx1 = left + (right - left) / 2;   

    auto pivot = a[idx1];

    Index i = left;
    Index j = right;

    Index index1 = left - 1;
    Index index2 = right + 1;

    while (i <= j)
    {
        while (compare(a[i], pivot))
            ++i;

        while (compare(pivot, a[j]))
            --j;

        if (i < j)
        {
            if (compare(pivot, a[i]))
            {
                if (compare(a[j], pivot))
                {
                    std::swap(a[i], a[j]); // a[i] != pivot and a[j] != pivot
                }
                else
                {
                    std::swap(a[i], a[j]);  // a[i] != pivot and a[j] == pivot
                    std::swap(a[++index1], a[i]);
                }
            }
            else if (compare(a[j], pivot)) // a[i] == pivot a[j] != pivot
            {
                std::swap(a[i], a[j]);
                std::swap(a[j], a[--index2]);
            }
            else // a[i] == pivot and a[j] == pivot
            {
                std::swap(a[++index1], a[i]);
                std::swap(a[j], a[--index2]);
            }

            ++i;
            --j;
        }
        else if (i == j)
        {
            j = i - 1;
            i++;
            break;
        }
    }
   
    for (Index k = left; k <= index1; k++)
    {
        std::swap(a[k], a[j--]);       
    }

    for (Index k = right; k >= index2; k--)
    {
        std::swap(a[i++], a[k]);       
    };

    ThreeWayQuickSort(a, a + (j + 1), compare);
    ThreeWayQuickSort(a + i, finish, compare);
}

双轴分区

该方案类似于 Vladimir Yaroslavskiy [11] 提出的方法。我对其进行了轻微的简化和修改。其基本思想是选择两个基准值，并创建三个分区。以下是修改的主要部分：根据基准值是否相同，有两种处理方法。如果基准值不同，并且我们将它们排序，使得 compare(pivot1, pivot2) 为 true（我们称 pivot1 “小于” pivot2），则会创建以下分区

“小于或等于”pivot1 的元素 (!compare(pivot1,a[i]) 为 true)；
介于 pivot1 和 pivot2 之间的元素 (compare(pivot1,a[i]) && compare(a[i],pivot2) 为 true)；
“大于或等于”pivot2 的元素 (!compare(a[i],pivot2) 为 true)。

如果所选的基准值相同，分区会略有不同

“小于”pivot1 的元素 (compare(a[i],pivot1) 为 true)；
等于 pivot1（显然也等于 pivot2）的元素 (!compare(pivot1,a[i]) && !compare(a[i],pivot1) 为 true)；
“大于”pivot1 的元素 (compare(pivot1,a[i]) 为 true)。

如果基准值相等，显然第二个分区不需要排序。

以下是双轴快速排序的 C++ 递归实现

template <class Iterator, class Comparison = std::less<>>
void DualPivotQuickSort(Iterator  a, Iterator finish, Comparison compare = Comparison())
{
    Index right = (finish - a) - 1;
    Index left = 0;

    if (right <= left)
    {
        return;
    }

    auto idx1 = left + (right - left) / 3;
    auto idx2 = right - (right - left) / 3;

    std::swap(a[idx1], a[left]);
    std::swap(a[idx2], a[right]);

    if (compare(a[right], a[left]))
    {
        std::swap(a[left], a[right]);
    }

    if (right - left == 1)
    {
        return;
    }

    auto pivot1 = a[left];
    auto pivot2 = a[right];

    if (compare(pivot1, pivot2))
    {
        Index less = left + 1;
        Index greater = right - 1;

        while (!compare(a[greater], pivot2))
        {
            greater--;
        }

        while (!compare(pivot1, a[less]))
        {
            less++;
        }

        Index k = less;
        while (k <= greater)
        {
            if (!compare(pivot1, a[k]))
            {
                std::swap(a[k], a[less++]);
            }
            else if (!compare(a[k], pivot2))
            {
                std::swap(a[k], a[greater--]);
                while (!compare(a[greater], pivot2))
                {
                    greater--;
                }

                if (!compare(pivot1, a[k]))
                {
                    std::swap(a[k], a[less++]);
                }
            }
            k++;
        }

        std::swap(a[less - 1], a[left]);
        std::swap(a[greater + 1], a[right]);

        DualPivotQuickSort(a, a + less - 1, compare);
        DualPivotQuickSort(a + greater + 2, finish, compare);
        DualPivotQuickSort(a + less, a + greater + 1, compare);
    }
    else
    {
        // pivot1 == pivot2
        Index less = left + 1;
        Index greater = right - 1;

        while (compare(pivot1, a[greater]))
        {
            greater--;
        }

        while (compare(a[less], pivot1))
        {
            less++;
        }
       
        Index k = less;
        while (k <= greater)
        {
            if (compare(a[k], pivot1))
            {
                std::swap(a[k], a[less++]);
            }
            else if (compare(pivot1, a[k]))
            {
                std::swap(a[k], a[greater--]);
                while (compare(pivot1, a[greater]))
                {
                    greater--;
                }

                if (compare(a[k], pivot1))
                {
                    std::swap(a[k], a[less++]);
                }
            }
            k++;
        }

        std::swap(a[less - 1], a[left]);
        std::swap(a[greater + 1], a[right]);
       
        DualPivotQuickSort(a, a + less - 1, compare);
        DualPivotQuickSort(a + greater + 2, finish, compare);
    }
}

效率的初步指标：计算比较和交换次数

在本节中，我将考察所选分区方法的比较次数和交换次数。这将为这些方法的速度提供一个粗略的指示。

我测试了快速排序方法在包含1000万个随机生成元素、不同数量不同元素的向量上的表现。产生的比较次数如图1所示。当比较操作比交换操作耗时得多时（例如 std::vector<std::string> 的情况），这可以很好地指示速度。

图 1. 比较次数

我们可以看到，Hoare 快速排序对不同元素数量的依赖性较小，但在有大量重复元素时，其性能不如其他两种方法。三路快速排序在有许多重复元素时表现很好，但当重复元素数量减少时，其效率开始下降。

图 2 显示了交换次数。

图 2. 交换次数

三路快速排序的交换次数最少，除非不同元素的数量接近100%。

在图 3 中，我展示了比较次数和交换次数的总和。当比较和交换操作耗时大致相同时，这可以很好地指示速度，例如 std::vector<double> 的情况。

图 3. 比较次数加交换次数。对 std::vector<double> 的速度有很好的指示作用

使用栈的实现

为了使用栈，Hoare 分区本身可以实现如下

template <class Elem, class Comparison>
struct HoarePartition
{
    ParamList operator()(Elem *a, Index left, Index right, Comparison compare)
    {
        Index i = left;
        Index j = right;
        Elem pivot = a[left+(right-left)/2];

        while (i <= j)
        {
            while (compare(a[i], pivot))
                ++i;

            while (compare(pivot, a[j]))
                --j;

            if (i <= j)
            {
                std::swap(a[i], a[j]);
                ++i;
                --j;
            }
        }

        return { {left,j}, {i, right} };
    }
};

对于其他分区方案，实现将是相似的。值的范围被推入一个 ParamList 对象，在那里它们按范围大小的降序排列。当值从 ParamList 对象移动到栈上时，最大的范围将首先被推入，这意味着，根据 LIFO（后进先出）访问规则，它将最后被处理。这将有助于最小化栈的大小。

多线程实现

这种方法类似于使用栈的实现。但是我们不是将值推入栈中，而是创建线程

const unsigned SortThreadCount = 7;

template <template<class, class> class Method, class Iterator, class Comparison>
void ParQuickSortRun(Iterator start, Iterator finish, Comparison compare)
{
    Index right = (finish - start) - 1;
    Index left = 0;

    if (right <= 0)
        return;

    typedef typename std::remove_reference<decltype(*start)>::type Elem;
    Elem* a = &*start;

    std::vector<std::thread> threads;

    if ((right-left) < 100000)
    {
        QuickSortRun<Method, Elem*, Comparison>(a + left, a + right + 1, compare);
        return;
    }

    Index range = (right - left) / SortThreadCount;
    
    Method<Elem, Comparison> method;

    while (true)
    {

        if (right - left < range)
        {
            threads.push_back(std::thread(QuickSortRun<Method, Elem*, Comparison>, a + left, a + right + 1, compare));
            break;

        }

        Index dist = (right - left);       
        Index i0 = left;
        Index i1 = left + dist / 3;       
        Index i2 = left + dist / 2;       
        Index i3 = right - dist / 3;       
        Index i4 = right;

        SmallSort(a, { i0,i1,i2,i3,i4 }, compare);

        ParamList params = method(a, left, right, compare);

        bool first = true;

        Index n = params.size();
        for (Index i = n - 1; i >= 0; i--)
        {
            QuickSortParams& p = params[i];
            if (first)
            {
                first = false;
                left = p.m_left;
                right = p.m_right;
            }
            else
            {
                threads.push_back(std::thread(ParQuickSortRun<Method, Iterator, Comparison>, start + p.m_left, start + p.m_right+1, compare));
            }                       
        }

        if (first)
            break;
    }

    for (unsigned i = 0; i < threads.size(); i++)
    {
        threads[i].join();
    }
}

有一个常量 SortThreadCount，我将其设置为 7。它对于 2 核和 4 核处理器似乎都工作得很好。但显然，对于拥有更多核心的处理器，这个常量值应该增加。如果第一个和最后一个索引之间的距离小于 100,000，我们不使用多线程。然后，与栈的情况一样，我们对选定的 5 个元素进行排序并调用该方法。当返回范围列表时，最后一个范围用于当前线程，其余的用于新线程。

循环继续，直到没有剩余范围，或者范围大小小于整个数组大小除以 SortThreadCount。在后一种情况下，将最后一次使用非多线程方法。循环结束后，ParQuickSortRun 函数必须等待所有线程终止。

基准测试

随机生成的数据

已进行以下测试以产生基准测试结果

对三种快速排序算法使用栈和多线程实现，并与 std::sort 进行比较；
所有测试均已在 VC++2015 和 GCC C++ 5.1 中为 i7-4790（4 核，3.6 GHz，8 GB 内存）编译；
所有测试均已在 GCC C++ 5.1 中为 i5-2410（2 核，2.3 GHz，6 GB 内存）编译；
考虑了三种类型的数组：std::vector<string>（字符串长度超过 71 个字符——比较慢，但交换快）、std::vector<double>（比较和交换都快）、std::vector<Block>（其中 Block 是一个包含 31 个字符数组的类——比较和交换都慢）。

std::vector<Block> 的测试

Block 类和比较函数的定义如下

struct Block
{
    static constexpr std::size_t N = 31;
    unsigned char x[N];
    Block(unsigned v = 0)
    {
        for (int i = 0; i < N; i++)
        {
            x[i] = (v >> i) & 1;
        }
    };
};

bool operator<(const Block& a, const Block& b)
{
    for (int i = 0; i < Block::N; i++)
    {
        if (a.x[i] < b.x[i])
            return true;
        if (a.x[i] > b.x[i])
            return false;
    }
    return false;
}

在 i7-4790 上使用 VC++ 的测试结果如图 4 所示，在 i7-4790 上使用 GCC C++ 的结果如图 5 所示，在 i5-2410 上使用 GCC C++ 的结果如图 6 所示。

图4。

图5。

图6。

我用“Par”来命名多线程实现。结果显示，在 4 核 i7 处理器上，多线程实现平均比其非多线程版本快 3.5 倍以上，在 2 核 i5 上快两倍以上。在所有情况下，双轴快速排序都比 Hoare 快速排序快。三路快速排序仅在某些不同元素非常少的情况下比双轴快速排序快。

VC++ 上的 std::sort 在性能上似乎与三路快速排序相似；而在 GCC C++ 上则与 Hoare 快速排序相似。

std::vector<std::string> 的测试

对 std::vector<std::string> 进行排序的测试结果如下：在 i7-4790 上使用 VC++ 的结果如图 7 所示，在 i7-4790 上使用 GCC C++ 的结果如图 8 所示，在 i5-2410 上使用 GCC C++ 的结果如图 9 所示。

图7。

图8。

图9。

这里的结果与块（Block）有些相似。双轴快速排序比 Hoare 快速排序快（当不同元素的数量接近数组大小时，速度几乎相同）。当不同元素的数量少于 1000 时，在某些情况下，双轴快速排序的效率略低于三路快速排序。

std::sort 的表现不如 VC++ 上的相应三路排序和 GCC C++ 上的 Hoare 排序。

std::vector<double> 的测试

对 std::vector<double> 进行排序的测试结果如下：在 i7-4790 上使用 VC++ 的结果如图 10 所示，在 i7-4790 上使用 GCC C++ 的结果如图 11 所示，在 i5-2410 上使用 GCC C++ 的结果如图 12 所示。

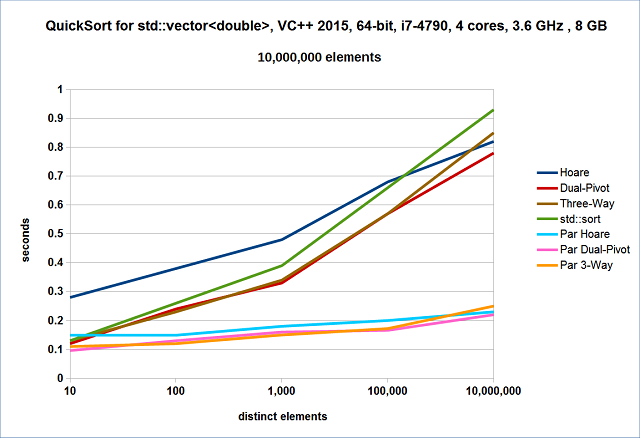
图10。

图11。

图12。

在这里，双轴快速排序击败了 Hoare 快速排序。在中等重复度范围内（不同元素在 100 到 100,000 之间），双轴快速排序比三路快速排序稍慢。GCC C++ 实现的 std::sort 比 Hoare 快速排序快，并且比单线程的双轴快速排序快。VC++ 的 std::sort 运行速度比单线程的三路快速排序慢。

与其他方法的比较

在这里，我想展示一些与其他方法的比较：Timsort [12-15]、Heapsort [8] (std::sort_heap) 和 Mergesort [8]。我将使用以下 Mergesort 的实现

    template<class Elem, class Comparison>
    void merge(Elem *v, Elem* a, Index left, Index right, Index rightEnd, Comparison compare)
    {
        Index temp = left, leftEnd = right - 1;
        Index start = left;

        for (Index i = start; i <= rightEnd; i++)
        {
            a[i] = std::move(v[i]);
        }

        while ((left <= leftEnd) && (right <= rightEnd))
        {
            if (compare(a[left], a[right]))
            {
                v[temp++] = std::move(a[left++]);
            }
            else
            {
                v[temp++] = std::move(a[right++]);
            }
        }
        while (left <= leftEnd)
        {
            v[temp++] = std::move(a[left++]);
        }

        while (right <= rightEnd)
        {
            v[temp++] = std::move(a[right++]);
        }
    }

    template<class Elem, class Comparison>
    void mSort(Elem *a, Elem* v, Index left, Index right, Index limit, Comparison compare)
    {
        if (left<right)
        {

            if (right - left < 32)
            {
                SmallSort(a, left, right, compare);
                return;
            }

            bool sorted = true;
            for (Index i = left; i < right; i++)
            {
                if (compare(a[i + 1], a[i]))
                {
                    sorted = false;
                    break;
                }
            }

            if (sorted)
                return;
           
            // checking for reverse-sorted
            bool reverse_sorted = true;
            for (Index i = left; i < right; i++)
            {
                if (compare(a[i], a[i + 1]))
                {
                    reverse_sorted = false;
                    break;
                }
            }

            if (reverse_sorted)
            {
                Index i = left;
                Index j = right;
                while (i < j)
                {
                    std::swap(a[i++], a[j--]);
                }
                return;
            };

            Index center = (left + right) / 2;
            std::thread th1;
            if (right - left > limit)
            {
                th1 = std::thread(mSort<Elem, Comparison>, a, v, left, center, limit, compare);
                mSort(a, v, center + 1, right, limit, compare);
                th1.join();
            }       
            else
            {
                mSort(a, v, left, center, limit, compare);
                mSort(a, v, center + 1, right, limit, compare);
            }       
            merge(a, v, left, center + 1, right, compare);
        }
    }

    template<class Iterator, class Comparison = std::less<>>
    void MergeSort(Iterator start, Iterator finish, Comparison compare = Comparison())
    {   
        Index right = (finish - start) - 1;

        if (right <= 0)
            return;

        typedef typename std::remove_reference<decltype(*start)>::type Elem;
        Elem* a = &*start;   

        Elem *temp = new Elem[right + 1];
        Index limit = (right + 1) / (SortThreadCount*2);
        mSort(a, temp, 0, right, limit, compare);
        auto heap2 = MemoryHeapUsed();
        delete[] temp;
    }

关键特性如下

合并时使用标准的移动赋值，这对于可移动对象（如字符串、容器）是高效的。
在排序之前，会检查每个片段是否已排序或逆序排序：这使得对振荡数据的排序更有效率；
使用了多线程。

对于 Timsort，我使用了 [14] 中提供的实现。我在附加的 zip 文件中对其进行了轻微修改：它有一个更简单的比较实现，使其运行速度比原始版本稍快。我还添加了测量算法使用的堆大小的功能。对随机生成的字符串进行排序的数据如图 13 所示。

图 13.

Timsort 在处理随机生成的字符串时没有任何优势。此外，在这些测试中，它使用了 479MB 到 532MB 的额外堆空间。在下一节中，当我讨论部分有序数据的基准测试时，我将更多地讨论 Timsort 和其他方法。归并排序不是最高效的，但表现相当不错。

部分有序的数据

在实践中，数据通常是相关的，甚至是部分有序的。我展示了两种类型的部分有序数据的测试

类型 1 - 振荡数据（基本上是正弦曲线），如图 14 所示；
类型 2 - 沿斜坡攀升的振荡数据（类似于 sin(x)+x），如图 15 所示。

图 14.

图 15.

我特别在包含大数据块的数组上测试了 Timsort，每个数据块包含 1000 字节。在某些测试中，Timsort 相对于其他排序方法具有优势，正如您在图 16 中所见。

图 16. 测试类型 1 的部分有序数据数组。每个元素包含 1000 字节。

您可以在这里看到，当存在大量重复项时，Timsort 表现不佳，但随着重复项数量的减少，其性能会显著提高。实际上，您可以看到归并排序的性能非常接近 Timsort。原因在于 Timsort 利用了归并排序算法。在这些测试中，当存在大量重复项时，Par Dual-Pivot 和 Par Three-Way 快速排序方法表现最佳。但当重复项很少时，Timsort 是最好的。

现在让我们看看类型 2 的部分有序数据。测试结果如图 17 所示。括号中的“斜率变化次数”表示图中斜率改变方向的次数：从“上升”到“下降”或反之。如果这个值为零，则表示数组是已排序或逆序排序的。在此图中，这意味着向量是按升序排序的。

图 17. 测试类型 2 的部分有序数据数组。在有 1,000,000 个不同元素的情况下，数据是有序的。

Timsort 在这里表现最好。它胜过了所有其他方法。但这是在重复元素非常少的情况下的。当所有元素都有序时，Timsort 的性能也是最好的：0.54 秒。但在这里，数据元素很大，交换它们需要一些时间。

我已经证明，对于包含类型 1 数据（振荡数据）且重复项很少的块向量，Timsort 表现良好。相比之下，当我们处理字符串数组时，交换操作只涉及交换指针，Timsort 虽然有时比非并行的快速排序方法表现更好，但并不能胜过多线程的快速排序方法——Par Hoare、Par Dual-Pivot 和 Par Three-Way。字符串的结果如图 18 所示。

图 18. 测试类型 1 的部分有序数据数组。每个元素类型为 std::string，这使得它们很容易交换。

在这里，当处理大量重复数据时，多线程三路排序的效果略好一些。但当重复数据减少时，Par Dual-Pivot 和 Par Hoare 则更优。对于双精度浮点值向量，你可能会发现类似的结果：并行快速排序方法是最快的。

关于 Timsort 和快速排序方法之间比较的几句话

堆空间：在大多数测试中，Timsort 在堆上分配了额外的 k*sizeof(elem)*N 字节（其中 0.125 <=k <= 0.5，N 是数组的大小）。例如，对于 1,000,000 个 1000 字节的块，此方法使用了 121MB 到 487MB 的堆空间。相比之下，快速排序需要大约 1024 字节用于栈，并且不使用任何额外的堆空间。
Timsort 擅长对部分有序的大数据块进行排序，而快速排序更适合对包含容器、简单类型和指针的数组进行排序，其中数据可能是完全随机的。在实践中，Timsort 适合对数据库数据进行排序。
快速排序可以很容易地并行化：而 Timsort 则更难做到这一点。目前还没有它的并行实现。我的感觉是，当涉及到并行实现时，它可能需要更多的堆空间。原则上，总是可以将数组分成几部分然后合并它们，但这需要额外的堆空间 [16]。快速排序可以很容易地并行化，并利用多核处理器的优势。
对于有大量重复元素的数组，双轴快速排序和三路快速排序是迄今为止讨论过的方法中最快的。

一个真实世界的问题：从文本中提取单词并按字母顺序呈现

这里有一个实际问题：从文本中提取所有不同的单词并按升序排序。我们如何存储最终结果（一个有序集合或一个向量）并不重要。结果如图 19 所示。

具体问题是这样的。给定一个包含来自文本的 150 万个单词的向量，这些单词已经转换为大写。任务是将其转换为一个按字母顺序排列的去重单词集合。在这种情况下，结果集合将包含 24,355 个单词。我使用了由亚历山大·仲马（Alexandre Dumas）的几本书籍合并而成的文本 [17]。我尝试了其他欧洲语言的文本：结果类似。

图 19. 从文本中提取不同的单词并进行排序

例如，对于 Hoare 快速排序，我测量了以下代码的执行时间

HoareQuicksort(std::begin(words), std::end(words));
auto it = std::unique(words.begin(), words.end());
words.erase(it, words.end());

对于 std::set，测量了以下时间

std::set<std::string> st;
for (auto& x : words)
{
   st.insert(std::move(x));
}

与一些读者可能预期的相反，使用 std::set 并不是最快的方法。Timsort 和 Heapsort 是最慢的。而多线程的双轴快速排序和三路快速排序是最快的。

结论

双轴快速排序在所有情况下都比 Hoare 快速排序快。在有大量重复元素的情况下，三路快速排序可能比双轴快速排序稍快，但当重复元素很少（不同元素的数量超过数组大小的 95%）时，双轴快速排序是赢家。多线程实现的平均速度提升大致与核心数量成正比。由于我们生活在一个多核处理器的世界里，如果 C++ 标准库能提供多线程排序算法就好了。

Using the Code

所有附加的代码都应该在开启优化的情况下编译。对于 GCC C++，建议使用以下选项

g++ -m64 -Ofast -march=native -funroll-loops -ffast-math -std=c++14 %1.cpp -o %1.exe

对于 VC++，我建议使用以下选项：

此外，您可以考虑使用以下选项

启用增强指令集高级向量扩展 2 (/arch:AVX2)

主要修订

2015年8月31日。初版。
2015年9月6日。添加了与 Timsort、Mergesort 和 Heapsort 的比较；以及部分有序数据的基准测试。
2015年9月13日。在这些示例中使用了标准的堆排序（结合了std::make_heap 和std::sort_heap）。提供了一个不同的、更高效的归并排序实现。增加了一个真实世界的例子：从文本中提取不同的单词。