Bing Silverlight 地图中贝塞尔曲线

• 下载 MapBezier 示例 Silverlight 应用程序 - 157.53 KB

引言

Bing Maps Silverlight 控件库有一个 MapPolyline 类，用于在地图上显示连接的点。我希望我的点能平滑连接，但没有现成的支持，所以我开发了一个自定义控件，它派生自 MapShapeBase [^] 类。

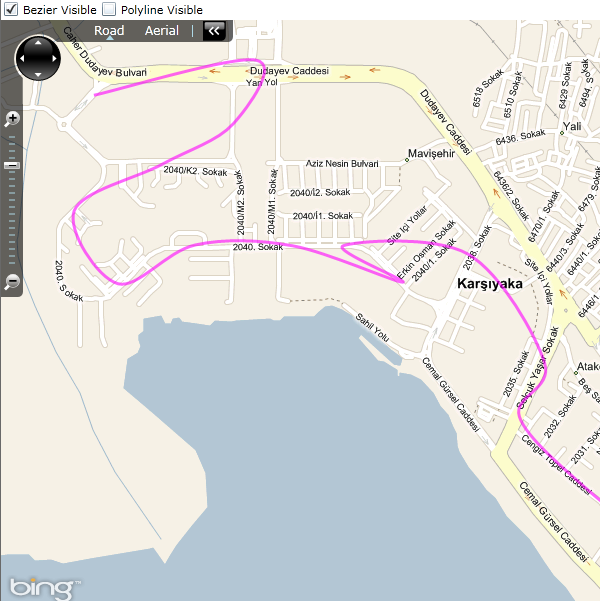
背景

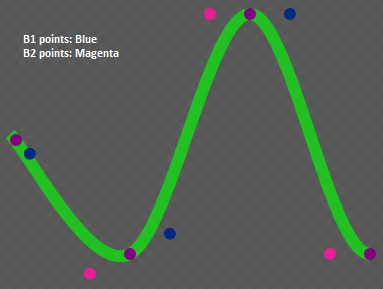
每个与 Expression Blend 或 Gimp 足够长时间打交道的开发人员都知道，通过实验，贝塞尔曲线是如何工作的。 基本上，三次贝塞尔曲线有一个起始点（P1），两个控制点（B1，B2）和一个结束点（P2）。

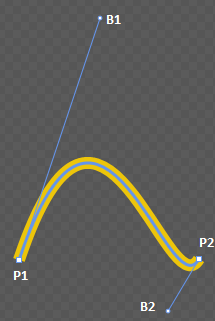
定义三次贝塞尔曲线的公式是

P(t) = (1-t)3P1 + 3(1-t)2tB1 + 3(1-t)t2B2 + t3P2

其中 t 在区间 [0,1] 中。 乘以 P1，B1，B2，P2 的项称为三次贝塞尔曲线的基函数。 我们的点决定了曲线包含多少这些基函数。

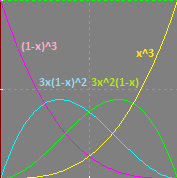
问题是我们需要计算控制点的坐标，以便我们的兴趣点在曲线上。

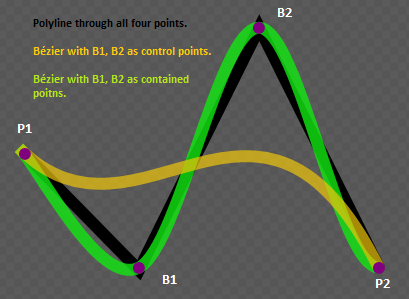
那么我们如何计算这些控制点呢？ 经过研究（阅读谷歌搜索），我找到了 cardinal splines [^] 和 Catmull-Rom splines [^] 。 似乎 Catmull-Rom 样条线的每个控制点都在曲线上，它也是一条贝塞尔曲线，这意味着我们可以将其用作 PathGeometry [^]，带有 Silverlight 的 Path 对象。

计算控制点

如果我们将 cardinal splines [^] 页面中的公式重写如下，我们可以轻松计算控制点。

导数

P'0 = (P1 - P0) / a
P'i = (Pi+1 - Pi-1) / a   where  i in [1, n-1]
P'n = (Pn - Pn-1) / a

控制点

B1i = Pi + P'i / 3
B2i = Pi+1 - P'i+1 / 3

Using the Code

计算贝塞尔点的该方法如下。 GetB1 和 GetB2 是上述公式的直接实现。

    private PointCollection GetBezierPoints(PointCollection pts, double tension)
        {
            PointCollection ret = new PointCollection();

            for (int i = 0; i < pts.Count; i++)
            {
                // for first point append as is.
                if (i == 0)
                {
                    ret.Add(pts[0]);
                    continue;
                }

                // for each point except first and last get B1, B2. next point. 
                // Last point do not have a next point.
                ret.Add(GetB1(pts, i - 1, tension));
                ret.Add(GetB2(pts, i - 1, tension));
                ret.Add(pts[i]);
            }

            return ret;
        }

要在 Silverlight 中使用从 GetBezierPoints 方法返回的 PointCollection，我们需要用 BezierSegments 构建一个 Path。

private PathFigure GetBezierSegments(PointCollection pts, double tension)
    {
        PathFigure ret = new PathFigure();
        ret.Segments.Clear();
        ret.IsClosed = false;

        var bzPoints = GetBezierPoints(_projectedPoints, tension);

        // First point is the starting point.
        ret.StartPoint = bzPoints[0];

        for (int i = 1; i < bzPoints.Count; i += 3)
        {
            ret.Segments.Add(new BezierSegment()
            {
                Point1 = bzPoints[i],       // B1 control point.
                Point2 = bzPoints[i + 1],   // B2 control point.
                Point3 = bzPoints[i + 2]    // P2 start / end point.
            });
        }

        return ret;
    }

并在 MapBezier 中使用此 PathFigure，如下所示

// Create a new PathGeometry.
var pGeo = new PathGeometry();

// Add the Bezier PathFigure to the PathGeometry.
pGeo.Figures.Add(GetBezierSegments(_projectedPoints, Tension));

// Set data of the Path to the created PathGeometry.
((Path)EncapsulatedShape).Data = pGeo;

您可以在 silverlight XAML 文件中使用 MapBezier 类，就像 MapPolyline 和 MapPolygon 类一样。 请参阅附带的示例以获取 Silverlight 应用程序的示例。

<m:Map x:Name="myMap" CredentialsProvider="***">
    <m:MapLayer x:Name="layerDurak" >
         <local:MapBezier Tension="2" x:Name="plDurakGidis" Stroke="Orange" 
    StrokeThickness="3" Opacity=".6" Locations="{Binding MyLocations, Mode=OneWay}" />
    </m:MapLayer>
</m:Map>

注意：需要 Bing Maps Silverlight SDK [^] 才能编译示例应用程序。

关注点

与 Bing Maps Silverlight 控件工具包一起使用很有趣，我希望 MapBezier 是您正在寻找的东西。

历史

• 初始文章。 2010 年 8 月 30 日 - 本文也可在 我的博客 上找到。