关于凸多面体、碰撞检测和单纯形法

Andreas Michael Kreuzer

4.98/5 (24投票s)

2016年5月19日

CPOL

29分钟阅读

36606

767

本文讨论使用单纯形法进行凸多面体的碰撞检测。

引言

几周前，我在本网站上偶然发现了一篇关于检查3D点是否在凸多边形内的文章（https://codeproject.org.cn/Articles/1065730/Point-Inside-Convex-Polygon-in-Cplusplus）。阅读这篇文章让我回想起，我曾想出一个算法，也能解决这个问题，但最初是为其他问题设计的， namely for convex polytopes 的碰撞检测。

由于这个网站在过去几年中对我帮助很大，我认为是时候回馈一些东西了。鉴于所讨论的算法出于某种原因似乎并不广为人知或广泛使用，我认为在此将其记录下来是一个好主意。我也必须承认，与其它算法相比，所介绍的算法会存在一些缺点，但我相信如果以适当的方式使用，仍然可以从中受益。

背景

所介绍的算法基于一些数学概念，据我所知，这些概念属于数学或计算机科学专业学生的标准教育范畴，因此理解起来应该不难。除此之外，我必须承认文章会包含一些数学内容。所以，如果有人不太喜欢数学，阅读这篇文章可能会有些困难。此外，每当我使用公知的数学概念、定义和定理时，我都不会详细解释或描述所有内容，以保持文章的简洁，但会在需要时添加指向专门网站的链接，以提供更多信息。

重要须知

如上所述，该算法是为凸多面体的碰撞检测设计的。它是在三维实空间中使用的。尽管如此，在开始之前，有三件重要的事情需要说明。

首先，该算法将以更通用的方式介绍，因为它也适用于n维实空间。

其次，该算法作为一个整体并不是全新的。它只是将一些已广为人知的概念组合在一起。我个人不知道为什么它以前没有以类似的方式使用，或者至少在我研究它并查阅书籍、文章和互联网时，我没有找到这种算法的此类应用。因此，我鼓励大家，如果您能找到任何额外的缺点、问题、优点或任何其他信息，说明此算法为何可能是或不是一个好主意，请告知我。

第三，除了上面写的内容之外，该算法对于凸多面体是有效的且精确的！

在我开始介绍文章的实际内容之前，还有最后一件事：请不要因为我的英语不好而过于苛刻，因为我不是以英语为母语的人。

开始吧！

理论

本文的这一部分将介绍算法所需的理论。之所以添加这一节，是因为尚不清楚所得算法为何能解决碰撞检测问题。

现在，假设我们有两个有界闭凸多面体 $K$ 和 $L \subset \mathbb{R}^{n}$，其中 $n \in \mathbb{N}$。现在的问题是：这两个多面体是否会发生碰撞？为了回答这个问题，我们开始思考多面体以及它们如何发生碰撞。这将引出其他问题：如何表示一个多面体？碰撞意味着什么？等等...

因此，算法背后的理论介绍将分为三个部分。首先，我们将简要讨论凸多面体，然后阐明碰撞的含义，最后，我们将通过使用单纯形法来解决问题并回答碰撞问题。

凸多面体

关于什么是凸多面体以及三维实空间中的例子，如立方体、四面体、棱锥等，请参阅 https://en.wikipedia.org/wiki/Polytope。另外，我们关心的多面体应始终是有界闭的。在多面体术语的一些定义中，这一点已经包含在内。我在此说明这一点是为了清楚地说明我们在谈论什么。为了简单起见或作为示例，在接下来的部分中可以考虑两个立方体或盒子。此外，下面图片中给出了一些多面体的示例。

Sample polytopes

因此，设 $K$ 和 $L \subset \mathbb{R}^{n}$，其中 $n \in \mathbb{N}$。根据明可夫斯基定理（https://de.wikipedia.org/wiki/Satz_von_Minkowski），一个有界闭凸多面体 $K \subset \mathbb{R}^{n}$ 是其极点或顶点的凸包。例如，三维立方体的八个顶点的凸包就是立方体本身。

请注意，我引用了德语维基百科页面，因为明可夫斯基定理在德语和英语中有两个不同的定理，而目前维基百科上没有相应的英语页面。此外，您可以在这里 https://en.wikipedia.org/wiki/Convex_hull#Convex_hull_of_a_finite_point_set 找到所需的陈述（英文）。

现在，假设我们有 $K$ 和 $L$ 的顶点集。我们称这些集合为 $S$ 和 $T$。同时请注意，根据定义，这两个集合的基数都是有限的。这导致了 $K$ 和 $S$ 的以下结果。

$\begin{align} S & \subseteq K, \\ K & = conv(S) = \{ \sum _{i=1} ^{\vert S \vert} \lambda _{i} s _i \, \vert \, s _i \in S, \lambda _i \geq 0 \, \forall \, i, \sum _{i=1} ^{\vert S \vert} \lambda _i = 1 \} \end{align}$

对于 $L$ 和 $T$ 也分别适用。

这主要表明，我们可以将多面体的每个点表示为其顶点的凸组合，并将多面体本身表示为其顶点的凸包。

现在，让我们添加一些将在下一节中需要的关于凸多面体的额外信息。我们定义两个集合的闵可夫斯基和与闵可夫斯基差。如果我们有两个集合 $V$ 和 $W \subset \mathbb{R}^{n}$，那么它们的闵可夫斯基和定义为

$V + W := \{ v + w \, \vert \, v \in V, w \in W \}$

它们的闵可夫斯基差定义为

$V - W := \{ v - w \, \vert \, v \in V, w \in W \}$

同样，两个凸集的闵可夫斯基和或差仍然是一个凸集。此外，两个集合的闵可夫斯基和或差的凸包等于它们凸包的闵可夫斯基和或差。更多信息可以在这里找到 https://en.wikipedia.org/wiki/Minkowski_addition。

这意味着对于我们上面的凸多面体， $K-L$ 是一个凸集，可以表示为

$K - L = conv(S) - conv(T) = conv(S-T) = $

此外，我们想为任何集合 $W \subset \mathbb{R}^{n}$ 定义 $-W$。

$-W := \{ -w \, \vert w \in W \}$

根据定义，这也意味着

$\vert -W \vert = \vert W \vert$

结合以上内容，对于任何有限集 $V \subset \mathbb{R}^{n}$，我们得到以下结果。

$\begin{align} -conv(V) & = - \{ \sum _{i=1} ^{\vert V \vert} \lambda _{i} v _i \, \vert \, v _i \in V, \lambda _i \geq 0 \, \forall \, i, \sum _{i=1} ^{\vert V \vert} \lambda _i = 1 \} \\ & = \{ - \sum _{i=1} ^{\vert V \vert} \lambda _{i} v _i \, \vert \, v _i \in V, \lambda _i \geq 0 \, \forall \, i, \sum _{i=1} ^{\vert V \vert} \lambda _i = 1 \} \\ & = \{ \sum _{i=1} ^{\vert V \vert} - \lambda _{i} v _i \, \vert \, v _i \in V, \lambda _i \geq 0 \, \forall \, i, \sum _{i=1} ^{\vert V \vert} \lambda _i = 1 \} \\ & = \{ \sum _{i=1} ^{\vert V \vert} \lambda _{i} (-v) _i \, \vert \, v _i \in V, \lambda _i \geq 0 \, \forall \, i, \sum _{i=1} ^{\vert V \vert} \lambda _i = 1 \} \\ & = \{ \sum _{i=1} ^{\vert V \vert} \lambda _{i} v _i \, \vert \, v _i \in -V, \lambda _i \geq 0 \, \forall \, i, \sum _{i=1} ^{\vert V \vert} \lambda _i = 1 \} \\ & = conv(-V) \end{align}$

在开始下一节之前，下面的图片展示了二维实空间中两个集合的闵可夫斯基和的图形示例。

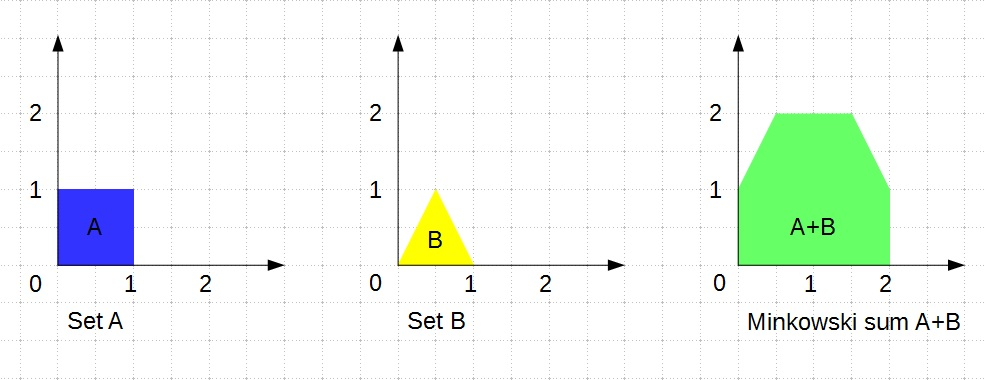
Sample Minkowski sum

碰撞检测

本节将定义在此上下文中碰撞检测的含义以及如何理解它。为此，我们将从对碰撞和碰撞的概念进行一些思考开始。

假设有两个任意物体，并想知道它们是否会发生碰撞。实际上，我们关心的是这两个物体是否接触或相交。这引出了我们可以识别两个物体是否碰撞的一种方式。为了回答这个问题，我们需要知道这两个物体之间的距离。如果它们的距离为0，则物体正在碰撞，否则则没有。

现在，假设有两个非空集合 $V$ 和 $W \subset \mathbb{R}^{n}$。设 $d$ 是 $\mathbb{R}^{n}$ 上的一个度量，这意味着

$\begin{align} (i) \, & d(v,w) \geq 0, \quad d(v,w) = 0 \Leftrightarrow v = w, \\ (ii) \, & d(v,w) = d(w,v), \\ (iii) \, & d(v,w) \leq d(v,u) + d(u,w), \\ & \forall \, u,v,w \in \mathbb{R}^{n} \end{align}$

这使我们能够使用度量来定义 $\mathbb{R}^{n}$ 中任意两点之间的距离 $dist$。此外，两个非空集合 $V$ 和 $W$ 之间的距离可以定义为

$dist(V,W) := inf \{ d(v,w) \, \vert \, v \in V, w \in W \}$

另外请注意，如果集合 $V$ 和 $W$ 是紧致的，则下确界可以用最小值代替。

总而言之，这是两个物体之间距离的一个相当直观的定义，并且我们有了一个很好的方法来明确定义两个物体是否碰撞。考虑到 $dist$ 函数的定义，这意味着 $V$ 和 $W$ 发生碰撞当且仅当存在至少一对点 $(v,w)$，其中 $v \in V$ 和 $w \in W$ 满足 $v = w$。这又可以重写为

$v = w \Leftrightarrow v - w = 0, \quad v \in V, w \in W, 0 \in \mathbb{R}^{n}$

最后一步是至关重要的，因为它允许我们使用不同的标准来检查 $V$ 和 $W$ 是否发生碰撞。如上所述，$V$ 和 $W$ 发生碰撞当且仅当它们至少有一个共同点。最后一个方程意味着我们可以通过回答以下问题来判断是否发生碰撞：

$Is \, 0 \in (V-W)?$

其中 $(V-W)$ 表示闵可夫斯基差。

现在，再次考虑我们上面的两个凸多面体 $K$ 和 $L \subset \mathbb{R}^{n}$，我们可以说，当且仅当

$\begin{align} & dist(K,L) = 0 \\ \Leftrightarrow \, & 0 \in (K-L) \end{align}$

这导致了另一个计算问题。由于 $dist$ 函数和闵可夫斯基差的定义，我们需要计算所有点对的所有距离或差值。不幸的是，这些点有无限多个。

但这并不是结束。幸运的是，我们可以使用一个非常巧妙的系统来描述这两个集合 $K$ 和 $L$。正如我们之前所学，这两个集合都可以用它们的顶点集 $S$ 和 $T$ 的凸包 $conv(S)$ 和 $conv(T)$ 来表示。因此，上面的式子可以重写为

$\begin{align} & dist(conv(S),conv(T)) = 0 \\ \Leftrightarrow \, & 0 \in (conv(S)-conv(T)) \\ \Leftrightarrow \, & 0 \in (conv(S)+conv(-T)) \end{align}$

这基本上意味着，我们现在正在寻找表示 $0 \in \mathbb{R}^{n}$ 的方法，该方法基于两个相同点的凸组合之和，其中一个凸组合包含 $S$ 中的点，另一个包含 $-T$ 中的点。这只会导出一个线性系统。

$\begin{align} \hat{A}x & = 0, \\ x & \geq 0, \, \sum _{i = 1} ^{\vert S \vert} x _i = 1, \, \sum _{i = \vert S \vert + 1} ^{\vert S \vert + \vert T \vert} x _i = 1 \end{align}$

其中 $\hat{A} \in \mathbb{R}^{n \times (\vert S \vert + \vert T \vert)}$，其列是 $S$ 和 $-T$ 的元素。因此，当且仅当这个线性系统有有效的解时，两个多面体 $K$ 和 $L$ 才会发生碰撞。

使这个线性系统更复杂的是对 $x$ 的约束。幸运的是，这些约束具有特殊的形式。观察最后两个约束，可以看到它们也可以表示为向量的乘积。

$\begin{align} a _{n+1} x & = 1, \\ a _{n+2} x & = 1, \end{align}$

其中向量 $a _{n+1}$ 和 $a _{n+2}$ 的元素 $a _{n+1, i}$ 和 $a _{n+2, i}$ 由下式给出

$\begin{align} a _{n+1, i} & = \left\{\begin{array}{lr} 1 & \forall \, 1 \leq & i & \leq \vert S \vert \\ 0 & \forall \, (\vert S \vert + 1) \leq & i & \leq (\vert S \vert + \vert T \vert) \end{array}\right. \\ a _{n+2, i} & = \left\{\begin{array}{lr} 0 & \forall \, 1 \leq & i & \leq \vert S \vert \\ 1 & \forall \, (\vert S \vert + 1) \leq & i & \leq (\vert S \vert + \vert T \vert) \end{array}\right. \end{align}$

这使我们能够将线性系统重写为

$Ax = b, \quad x \geq 0$

其中 $A \in \mathbb{R}^{k \times m}$ 是由 $\hat{A}$ 和在末尾添加的附加方程 $a _{n+1} x = 1$ 和 $a _{n+2} x = 1$ 组成的矩阵，$k = n + 2$， $m = \vert S \vert + \vert T \vert$， $b \in \mathbb{R}^{k}$ 由其元素定义为

$b _{i} = \left\{\begin{array}{lr} 0 & \forall \, 1 \leq & i & \leq n \\ 1 & \forall \, (n + 1) \leq & i & \leq k \end{array}\right.$

同样，当且仅当该线性系统有有效解时，两个多面体 $K$ 和 $L$ 才会发生碰撞。我们将这个方程及其约束称为问题 $P1$。

这似乎使我们变得更复杂了。但我们将了解到，这种碰撞检测问题的表示是关键。在下一节中，我们将研究单纯形法，从而揭示上述表示与单纯形法能够解决的问题是匹配的。

单纯形法

本节将讨论单纯形法如何帮助解决上述问题 $P1$。为此，至少需要对单纯形法有一些了解。您可以在这里 https://en.wikipedia.org/wiki/Simplex_algorithm 或这里 https://mathworld.net.cn/SimplexMethod.html 找到它的介绍。

由于单纯形法是一种线性优化方法，我们从一个线性优化问题开始。假设我们要最小化以下函数，同时满足给定约束。

$min \, f _{A} (x), \quad f _{A} (x) := e^{T}(b-Ax), \quad Ax \leq b, x \geq 0$

其中

$ A \in \mathbb{R}^{k \times m}, \quad e = \left(\begin{array}{lr} 1 \\ 1 \\ \vdots \\ 1 \\ 1 \end{array}\right) \in \mathbb{R}^{k}, \quad b = \left(\begin{array}{lr} 0 \\ \vdots \\ 0 \\ 1 \\ 1 \end{array}\right) \in \mathbb{R}^{k}, \quad k, m \in \mathbb{N}$

是固定的，并且正在寻找 $x \geq 0 \in \mathbb{R}^{m}$。我们将此问题称为 $P2$。

关于问题 $P2$，人们可能会问的第一个问题是，是否存在任何 $x \geq 0 \in \mathbb{R}^{m}$ 满足给定的约束。事实上，是存在的。那就是 $x = 0$。这是正确的，因为 $b \geq 0$（根据定义）并且对于 $x = 0$，有 $0 = Ax \leq b$。

现在，让我们仔细看看我们要最小化的函数。我们有

$f _{A} (x) := \underbrace{e^{T}}_{> 0}\underbrace{(b-Ax)}_{\geq 0}$

因此，无论哪个 $x \geq 0 \in \mathbb{R}^{m}$ 满足给定的约束并最小化给定的函数，对于最小值本身，我们有

$min f _{A} (x) \geq 0 \quad \forall x: Ax \leq b, x \geq 0$

此外，对于所有 $x \geq 0$，我们有

$min f _{A} (x) = 0 \Leftrightarrow Ax = b$

现在，再次看看我们上面的碰撞检测问题 $P1$。对于这个问题，我们不知道方程 $Ax = b$ 是否有任何解 $x \geq 0$，以及多面体是否真的会发生碰撞。但是，我们刚刚学到的非常简单：我们不必直接求解方程 $Ax = b$ 来决定碰撞问题，只需解决优化问题 $P2$ 即可。

假设我们找到了一个 $x^{\ast}$ 来解决优化问题，即它最小化 $f _{A} (x)$ 并满足给定的约束。如果得到的最小值为

$f _{A} (x^{\ast}) = 0$

我们直接得到 $Ax^{\ast} = b$，因此，由矩阵 $A$ 和相关线性系统表示的相应凸多面体 $K$ 和 $L$ 会发生碰撞。否则，我们得到最小值

$f _{A} (x^{\ast}) > 0$

因此， $Ax^{\ast} < b$，由于结果的最优性，这包含了多面体不碰撞的信息。

这是我们到目前为止所有工作的主要结果：优化问题可用于决定两个凸多面体之间的碰撞问题：如果优化问题的最小值为 $0$，则凸多面体发生碰撞，否则不发生碰撞。

顺便提一下，应该说明的是，由于 $b-Ax \geq 0 \in \mathbb{R} ^{k}$ 以及向量 $e$ 的给定选择，我们有 $f _{A} (x)$ 是向量 $b-Ax \in \mathbb{R} ^{k}$ 的 1-范数，即

$f _{A} (x) = e^{T}(b-Ax) = \| (b-Ax) \| _{1}$

现在，这里剩下的工作是理解单纯形法可用于解决线性优化问题 $P2$。

单纯形法用于解决以标准形式给出的问题。不幸的是，没有一个唯一的标准形式。不同的作者指的是不同的单纯形法标准形式。但是，每种标准形式都可以通过一些定义的变换转换为另一种。对于本文，我们将下面的优化问题称为单纯形法的标准形式。最小化

$c^{T}x$

在以下约束下

$Ax = b, \quad x \geq 0$

其中 $A \in \mathbb{R}^{k \times m}$，$b \in \mathbb{R}^{k}$， $c \in \mathbb{R}^{m}$ 是由常数值给出的，而 $x \in \mathbb{R}^{m}$ 是要寻找的变量向量。

这并非完全是我们应用单纯形法解决问题 $P2$ 的形式。首先，我们没有 $c^{T}x$，而是

$e^{T}(b-Ax) = e^{T}b - e^{T}Ax$

由于在问题 $P2$ 中 $e$ 和 $b$ 是常数，最小化上述表达式可以通过最小化

$-e^{T}Ax = (-A^{T}e)^{T}x$

因此，定义

$c:=-A^{T}e$

表明问题 $P2$ 中要最小化的函数不是问题。第二个要解决的问题是，在问题 $P2$ 中，我们有约束

$Ax \leq b$

而不是

$Ax = b$

幸运的是，单纯形法也可以应用于具有给定不等式约束的问题。这是通过引入所谓的松弛变量来实现的。每行引入一个松弛变量。对于问题 $P2$，我们引入 $k$ 个松弛变量将不等式变为等式。考虑到这些松弛变量并采用它们的线性系统，我们可以将不等式约束改写为线性系统

$\tilde{A}\tilde{x} = b$

其中 $\tilde{A} \in \mathbb{R}^{k \times q}$， $\tilde{x} \in \mathbb{R}^{q}$ 且 $q = m + k$， $I _k \in \mathbb{R}^{k \times k}$ 是单位矩阵，以及

$\tilde{A} := \left( A, I _k \right), \quad \tilde{x} := \left( \begin{array}{lr} x \\ 0 \\ \vdots \\ 0 \\ 1 \\ 1 \end{array} \right), \, x \in \mathbb{R}^{m} $

此外，对于这个最后的线性系统，我们已经知道一个有效的解，即通过在上面应用 $x = 0 \in \mathbb{R}^{m}$ 来得到。因此，这个线性系统可以转移到单纯形表，我们可以直接应用单纯形法来计算一个解。

有关此的更多详细信息，请参考例如 http://en.wikipedia.org/wiki/Simplex_algorithm 以及那里找到的进一步参考。

现在，我们有了回答两个给定凸多面体 $K$ 和 $L \subset \mathbb{R}^{n}$ 是否碰撞所需的一切。在下一节中，我们将列出要实现的算法。

算法

在上面的所有理论之后，我们来到了算法本身。结果证明，（给定单纯形法的实现）该算法相当简单。

判断两个凸多面体 $K$ 和 $L \subset \mathbb{R}^{n}$ 是否碰撞的算法

获取两个多面体的顶点。
检查是否有任何多面体或其顶点集为空集。
1. 如果上述情况为真，则没有碰撞，因为没有什么可以碰撞的 - 转到 END。
检查两个多面体或其顶点集是否仅由一个点组成。
1. 如果是，则检查这两个单点是否相等。
2. 如果两个点相同，则多面体碰撞 - 转到 END。
3. 如果两个点不相同，则多面体不碰撞 - 转到 END。
如果至少有一个多面体有两个或更多顶点，则应用单纯形法来如上所述判断碰撞。
1. 如果所得的最小值是 0，则两个多面体发生碰撞 - 转到 END。
2. 如果所得的最小值大于 0，则两个多面体不发生碰撞 - 转到 END。
END。

代码

此处介绍的代码只是算法的基本实现，是针对三维实空间编写的。我猜想可能并且会有其他更好的单纯形法实现。只需适应并使用它们即可。尽管如此，给出的代码是有效的，并且可以与一个测试应用程序一起下载。

代码本身实际上由三个类组成，只有一个类真正有趣。两个类实际上是为了包装实现的碰撞检测算法并方便使用。这两个类是 **ConvexPolyhedron.cs** 和 **ConvexPolyhedronExtensions.cs**。算法本身完全实现在 **LinearProgramming.cs** 类中。

ConvexPolyhedron.cs

#region Usings (3)

using System.Collections.Generic;
using System.Windows.Media.Media3D;
using System.Xml.Serialization;

#endregion // Usings (3)

namespace CollisionDetection
{
    /// <summary>
    /// This class is a simple class to represent a 3-dimensional convex polytope or
    /// convex polyhedron by its corners.
    /// </summary>
    public class ConvexPolyhedron
    {
        #region Public Non-Static Properties (2)

        /// <summary>
        /// A name for this convex polyhedron.
        /// </summary>
        [XmlElement]
        public string Name { get; set; } = string.Empty;

        /// <summary>
        /// The set of corners representing the convex polyhedron.
        /// </summary>
        /// <remarks>
        /// The polyhedron itself need not to be 3-dimensional. The dimension of the polyhedron
        /// depends on its given corners and can formally range from -1 to 3, where -1 is the
        /// dimension of the empty set, 0 is the dimension of a single point, 1 is the dimension
        /// of a line given by at least two points, and so on.
        /// </remarks>
        [XmlArray]
        public HashSet<Point3D> Corners { get; set; } = new HashSet<Point3D>();

        #endregion // Public Non-Static Properties (2)
    }
}

ConvexPolyhedronExtensions.cs

#region Usings (4)

using System;
using System.Collections.Generic;
using System.Linq;
using System.Windows.Media.Media3D;

#endregion // Usings (4)

namespace CollisionDetection
{
    /// <summary>
    /// This public static class contains extension methods for the class
    /// <see cref="ConvexPolyhedron"/>. The extension method includes methods to check if two
    /// convex polyhedra are colliding and if one convex polyhedron is a subset of another given
    /// convex polyhedron.
    /// </summary>
    public static class ConvexPolyhedronExtensions
    {
        #region Public Static Extension Methods (2)

        /// <summary>
        /// This method tests if the two given convex polyhdra <paramref name="convPolyA"/> and
        /// <paramref name="convPolyB"/> are colliding with each other or not.
        /// </summary>
        /// <param name="convPolyA">The first <see cref="ConvexPolyhedron"/> to be tested for
        /// a collision with the second one.</param>
        /// <param name="convPolyB">The second <see cref="ConvexPolyhedron"/> to be tested for
        /// a collision with the first one.</param>
        /// <returns>True if the two given convex polyhedra are colliding, otherwise false.
        /// </returns>
        public static bool CollidesWith(this ConvexPolyhedron convPolyA,
            ConvexPolyhedron convPolyB)
        {
            // Call the linear programming method that checks for a collision.
            return LinearProgramming.AreColliding(convPolyA?.Corners, convPolyB?.Corners);
        }

        /// <summary>
        /// This method test if the given <paramref name="setToTest"/> is a subset of the
        /// given <see cref="supposedSuperset"/>. If so, true is returned and false, otherwise.
        /// </summary>
        /// <param name="setToTest">The <see cref="ConvexPolyhedron"/> that is tested for being
        /// a subset.</param>
        /// <param name="supposedSuperset">The <see cref="ConvexPolyhedron"/> that is tested for
        /// being a superset.</param>
        /// <returns>True if the subset condition applies, false otherwise.</returns>
        /// <exception cref="T:System.ArgumentNullException">This exception is thrown if any of
        /// the given convex polyhedra or their set of corners describing them is null.
        /// </exception>
        public static bool IsSubsetOf(
            this ConvexPolyhedron setToTest,
            ConvexPolyhedron supposedSuperset)
        {
            // Declare local variable.
            bool result;

            // Check that the given sets are not null. If any, throw exception.
            if ((null == setToTest) || (null == setToTest.Corners))
            {
                throw new ArgumentNullException("setToTest",
                    "The object that represents the set that is tested"
                    + " for being a subset is null.");
            }

            if ((null == supposedSuperset) || (null == supposedSuperset.Corners ))
            {
                throw new ArgumentNullException("supposedSuperset",
                    "The object that represents the superset for testing is null.");
            }

            // Check if set to test is the empty set.
            if (setToTest.Corners.Any())
            {
                // If the set to test is not the empty set check if the supposed
                // superset is the empty set.
                if (supposedSuperset.Corners.Any())
                {
                    // Declare block local variable.
                    int loop;

                    // Both sets are not empty, hence, check in more detail using the
                    // collision check. This is done, by checking for each single corner
                    // of the set to test, if it is contained in the supposed superset.

                    // Set result to true at the beginning and test until done or
                    // result is set to false.
                    loop = 0;
                    result = true;
                    while (result && (setToTest.Corners.Count > loop))
                    {
                        // Check for collision, i.e. if current corner is in
                        // the supposed superset.
                        result &= LinearProgramming.AreColliding(
                            new HashSet<Point3D>()
                                {
                                    setToTest.Corners.ElementAt(loop)
                                },
                            supposedSuperset.Corners);
                        // Increment loop variable.
                        loop++;
                    }
                }
                else
                {
                   // If the supposed superset is the empty set, the result is false.
                   result = false;
                }
            }
            else
            {
                // The result is true if the supposed superset is the empty set and
                // false, otherwise.
                result = !supposedSuperset.Corners.Any();
            }

            // Return the result.
            return result;
        }

        #endregion // Public Static Extension Methods (2)
    }
}

LinearProgramming.cs

#region Usings (4)

using System;
using System.Collections.Generic;
using System.Linq;
using System.Windows.Media.Media3D;

#endregion // Usings (4)

namespace CollisionDetection
{
    /// <summary>
    /// This public static class implements support for linear programming methods.
    /// In this case the simplex method with the rule of Bland is implemented for the
    /// special case of collision detection.
    /// </summary>
    public static class LinearProgramming
    {
        #region Private Constants (3)

        /// <summary>
        /// The dimension of the space this implementation is meant to be used for.
        /// </summary>
        private const int DIMENSION = 3;

        /// <summary>
        /// The number of convexity constraints needed by the simplex method to calculate
        /// the result for the collision detection problem.
        /// </summary>
        private const int NUMBER_OF_CONVEXITY_CONSTRAINTS = 2;

        /// <summary>
        /// The number of equations to solve by the simplex method to decide the collision
        /// detection problem.
        /// </summary>
        private const int NUMBER_OF_EQUATIONS = LinearProgramming.DIMENSION
            + LinearProgramming.NUMBER_OF_CONVEXITY_CONSTRAINTS;

        /// <summary>
        /// The number of slack variables needed by the simplex method to calculate the
        /// result for the collision detection problem.
        /// </summary>
        private const int NUMBER_OF_SLACK_VARIABLES = LinearProgramming.DIMENSION
            + LinearProgramming.NUMBER_OF_CONVEXITY_CONSTRAINTS;

        #endregion // Private Constants (3)

        #region Public Static Read-Only Properties (1)

        /// <summary>
        /// This public static read-only member defines the default accuracy used to distinguish
        /// floating point values in this class.
        /// </summary>
        public static readonly double DEFAULT_EPSILON = 0.0001;

        #endregion // Public Static Read-Only Properties (1)

        #region Private Static Members (1)

        /// <summary>
        /// This private static member variable stores the currently defined accuracy of the class
        /// used to distinguish two different floating point values.
        /// </summary>
        private static double _epsilon;

        #endregion // Private Static Members (1)

        #region Public Static Properties (1)

        /// <summary>
        /// Gets or sets the accuracy used to distinguish floating point values in this class.
        /// </summary>
        /// <exception cref="T:System.ArgumentException">This exception is thrown if the given
        /// value that shall be set is 0 or less.</exception>
        public static double Epsilon
        {
            get { return _epsilon; }
            set
            {
                // Check that value is not 0 or less. If so, throw exception.
                if (0 >= value)
                {
                    throw new ArgumentException("The applied accuracy must not be 0 or less.");
                }

                // If the given value is positive, set it.
                _epsilon = value;
            }
        }

        #endregion // Public Static Properties (1)

        #region Static Constructor (1)

        /// <summary>
        /// The static constructor of the class setting the default accuracy as accuracy
        /// for distinguishing two different floating point values at creation.
        /// </summary>
        static LinearProgramming()
        {
            Epsilon = LinearProgramming.DEFAULT_EPSILON;
        }

        #endregion //Static Constructor (1)

        #region Public Static Methods (4)

        /// <summary>
        /// This method checks if the two given convex polyhedra each represented by a set
        /// of corners are colliding with each other or not.
        /// </summary>
        /// <param name="convPolyA">The first set of corners to be tested for a collision
        /// with the second one.</param>
        /// <param name="convPolyB">The second set of corners to be tested for a collision
        /// with the first one.</param>
        /// <returns>True if the two given convex polyhedra are colliding, otherwise false.
        /// </returns>
        /// <exception cref="T:System.ArgumentNullException">This exception is thrown if any
        /// of the given parameters is null.</exception>
        public static bool AreColliding(ISet<Point3D> convPolyA, ISet<Point3D> convPolyB)
        {
            // Declare local variable.
            bool result;

            // Check that given objects are not null.
            if (null == convPolyA)
            {
                throw new ArgumentNullException("convPolyA",
                    "The given set of points representing the first convex polyhedron is null.");
            }
            if (null == convPolyB)
            {
                throw new ArgumentNullException("convPolyB",
                    "The given set of points representing the second convex polyhedron is null.");
            }

            // Check for empty sets, because if any set is the empty set,
            // the result is false, as empty sets cannot collide with anything.
            if (!convPolyA.Any() || !convPolyB.Any())
            {
                result = false;
            }
            else
            {
                // If both sets are not the empty set, check if both contain only a single point.
                if ((1 == convPolyA.Count) && (1 == convPolyB.Count))
                {
                    // Declare block local variables.
                    Point3D pointA = convPolyA.ElementAt(0);
                    Point3D pointB = convPolyB.ElementAt(0);

                    // Check if points are the same with respect to the
                    // defined accuracy and set the result.
                    result = ((pointA.X - pointB.X) < LinearProgramming.Epsilon)
                        && ((pointA.Y - pointB.Y) < LinearProgramming.Epsilon)
                        && ((pointA.Z - pointB.Z) < LinearProgramming.Epsilon);
                }
                else
                {
                    // If at least one set contains more than one single point, use the
                    // simplex method to decide if the convex polyhedra represented by
                    // the given sets collide or not.
                    // 1.) Create initial tableau.
                    // 2.) Perform simplex method.
                    // 3.) Evaluate and return the result with respect to the given accuracy.
                    result =
                        LinearProgramming.PerformSimplexMethod(
                            LinearProgramming.CreateInitialTableau(
                                convPolyA, convPolyB)) < LinearProgramming.Epsilon;
                }
            }

            // Return the result.
            return result;
        }

        /// <summary>
        /// This method creates the initial tableau used by the simplex method to perform
        /// the collision check.
        /// </summary>
        /// <param name="convPolyA">The first set of corners to be tested for a collision
        /// with the second one.</param>
        /// <param name="convPolyB">The second set of corners to be tested for a collision
        /// with the first one.</param>
        /// <returns>Returns the initial tableau for the simplex method.</returns>
        /// <exception cref="T:System.ArgumentException">This exception is thrown in case
        /// something is wrong with the applied indices.</exception>
        public static double[,] CreateInitialTableau(
            ISet<Point3D> convPolyA, ISet<Point3D> convPolyB)
        {
            // Create the return variable.
            double[,] tableau = new double
                [LinearProgramming.NUMBER_OF_EQUATIONS + 1,
                convPolyA.Count + convPolyB.Count
                    + LinearProgramming.NUMBER_OF_SLACK_VARIABLES + 1];

            // The tableau is filled in several steps.

            // 1.) Fill in the values for the points of the first polyhedron, column by column.
            for (int k = 0; k < convPolyA.Count; k++)
            {
                tableau[1, k] = convPolyA.ElementAt(k).X;
                tableau[2, k] = convPolyA.ElementAt(k).Y;
                tableau[3, k] = convPolyA.ElementAt(k).Z;
                tableau[4, k] = 1.0;
                tableau[5, k] = 0.0;
            }

            // 2.) Fill in the values for the points of the second polyhedron, column by column.
            //     Do not forget to multiply the values of the points by -1.
            for (int k = 0; k < convPolyB.Count; k++)
            {
                int k_shifted = k + convPolyA.Count;
                tableau[1, k_shifted] = -convPolyB.ElementAt(k).X;
                tableau[2, k_shifted] = -convPolyB.ElementAt(k).Y;
                tableau[3, k_shifted] = -convPolyB.ElementAt(k).Z;
                tableau[4, k_shifted] = 0.0;
                tableau[5, k_shifted] = 1.0;
            }

            // 3.) Fill the cost row, i.e. the first row of the tableau
            //     for the points added so far.
            for (int k = 0; k < (convPolyA.Count + convPolyB.Count); k++)
            {
                tableau[0, k] = 0.0;
                for (int i = 1; i < tableau.GetLength(0) ; i++)
                {
                    tableau[0, k] -= tableau[i, k];
                }
            }

            // 4.) Generate the columns for the slack variables, i.e. the identity matrix
            //     in 5 times 5 real space including 0 values for the cost row.
            for (int k = (convPolyA.Count + convPolyB.Count);
                k < (convPolyA.Count + convPolyB.Count 
                    + LinearProgramming.NUMBER_OF_SLACK_VARIABLES);
                k++)
            {
                tableau[0, k] = 0.0;
                for (int i = 1; i < tableau.GetLength(0); i++)
                {
                    tableau[i, k] =
                        ((k - convPolyA.Count - convPolyB.Count + 1) == i)
                            ? 1.0 : 0.0;
                }
            }

            // 5.) Fill the full column for the vector b of the linear system introduced.
            tableau[0, convPolyA.Count + convPolyB.Count
                + LinearProgramming.NUMBER_OF_SLACK_VARIABLES] = 0.0;
            for (int i = 1; i < tableau.GetLength(0); i++)
            {
                tableau[i, convPolyA.Count + convPolyB.Count
                    + LinearProgramming.NUMBER_OF_SLACK_VARIABLES]
                        = (LinearProgramming.DIMENSION >= i) ? 0.0 : 1.0;
                tableau[0, convPolyA.Count + convPolyB.Count 
                    + LinearProgramming.NUMBER_OF_SLACK_VARIABLES]
                        -= tableau[i, convPolyA.Count + convPolyB.Count
                            + LinearProgramming.NUMBER_OF_SLACK_VARIABLES];
            }

            // Return the tableau.
            return tableau;
        }

        /// <summary>
        /// This method performs the simplex method on the given tableau to evaluate
        /// an optimized result for a minium problem.
        /// </summary>
        /// <remarks>
        /// Note that the parameter <paramref name="tableau"/> is changed during calculation.
        /// </remarks>
        /// <param name="tableau">The initial tableau to apply the simplex method on.</param>
        /// <returns>Returns the calculated minimum.</returns>
        public static double PerformSimplexMethod(double[,] tableau)
        {
            // Declare local variables.
            double infimum;
            int loop;
            int pivotColumn;
            int pivotRow;
            int numberOfColumns = tableau.GetLength(1);
            int numberOfRows = tableau.GetLength(0);
            int limitOfLoops = numberOfColumns * numberOfRows;
            int baseSlackVariableIndex = tableau.GetLength(1)
                - LinearProgramming.NUMBER_OF_EQUATIONS - 1;
            int[] basicIndices = new int[LinearProgramming.NUMBER_OF_EQUATIONS];

            // Define infimum at the beginning to be the maximum value possible due
            // to setup of the equations.
            infimum = 2.0;

            // Initially fill the array of basic indices with the column indices
            // of the slack variables.
            for (loop = 0; loop < LinearProgramming.NUMBER_OF_EQUATIONS; loop++)
            {
                basicIndices[loop] = baseSlackVariableIndex + loop;
            }

            // Get first pivot element to start the simplex method with.
            SelectPivotByBlandsRule(tableau, basicIndices, out pivotRow, out pivotColumn);

            // Start looping and perform the simplex method. There are three stop criteria.
            // 1.) The result is less than the defined epsilon, i.e. the result is
            //     supposed to be 0 and
            //     the objects are colliding. Note that this condition is negated for checking.
            // 2.) If the column index is equal to or greater than the number of columns in the
            //     tableau or the row index is equal to or greater than the number of rows in
            //     the tableau, this means we are done, as there is no more pivot left. Note that
            //     this condition is negated for checking.
            // 3.) We stop after a defined number of loops to ensure we stick to a linear number
            //     of loops and do not end up in an exponential number of loops. We decided to
            //     stop after number of columns times number of rows in the tableau.
            while ((infimum >= LinearProgramming.Epsilon)
                && (pivotColumn < numberOfColumns)
                && (pivotRow < numberOfRows)
                && (limitOfLoops > loop))
            {
                // Check results of pivot selection.
                if ((0 > pivotColumn) || (0 > pivotRow))
                {
                    // If the column or row index for the pivot is less than 0 there
                    // was an error on selection. Throw therefore an exception.
                    throw new ArgumentException("Something went wrong!"
                        +" The pivot selection failed with an error!!!");
                }

                // Due to checking the stop criteria in the header of the loop, the
                // remaining case is that we have to perform a simplex step. Also, this
                // is not done in an else case due to exception above.

                // Update the base indices, i.e. the element at the index of the pivot
                // row (-1 one due to 0-indexed array) is replaced by the given pivot column.
                basicIndices[pivotRow - 1] = pivotColumn;

                // Get pivot element.
                double pivot = tableau[pivotRow, pivotColumn];

                // 1.) Divide pivot row by pivot element, set pivot element to 1.0 directly.
                for (int i = 0; i < numberOfColumns; i++)
                {
                    tableau[pivotRow, i] = i == pivotColumn ? 1.0 : tableau[pivotRow, i] / pivot;
                }

                // 2.) Update all other rows by subtracting the pivot row multiplied by the
                //     current rows entry in the pivot elements column.
                for (int k = 0; k < numberOfRows; k++)
                {
                    if (k != pivotRow)
                    {
                        double temp = tableau[k, pivotColumn];
                        for (int i = 0; i < numberOfColumns; i++)
                        {
                            tableau[k, i] = i == pivotColumn
                                ? 0.0
                                : tableau[k, i] - temp * tableau[pivotRow, i];
                        }
                    }
                }

                // Adapt all four values controlling the loop conditions.

                // Get the new overall cost value and replace it in the infimum variable.
                // Be aware that for getting the infimum, the cost value must be multiplied by -1.
                infimum = -tableau[0, numberOfColumns - 1];

                // Select next pivot element.
                SelectPivotByBlandsRule(tableau, basicIndices, out pivotRow, out pivotColumn);

                // Increment loop variable.
                loop++;
            }

            // Return the calculated infimum.
            return infimum;
        }

        /// <summary>
        /// This method performs the selection of a pivot element for the next step
        /// in the simplex method based on Bland's rule. The pivot is identified by the output
        /// parameters <paramref name="row"/> and <paramref name="column"/>.
        /// </summary>
        /// <remarks>
        /// In case the values returned by the method are -1 an error occurred. In case the
        /// returned values match the number of rows and columns in the given tableau, there is
        /// no other pivot element left. This can be used as a stop criterion for the simplex
        /// method.
        /// </remarks>
        /// <param name="tableau">The tableau to select the next pivot element for.</param>
        /// <param name="basicIndices">The basic indices valid for the current simplex
        /// step.</param>
        /// <param name="row">The row of the pivot element, 0-based.</param>
        /// <param name="column">The column of the pivot element, 0-based.</param>
        public static void SelectPivotByBlandsRule(
            double[,] tableau,
            int[] basicIndices,
            out int row,
            out int column)
        {
            // Please note for the following, that all checks are made with
            // respect to the defined epsilon!

            // Declare local variables.
            int loop;
            int numberOfPivotRows;
            int numberOfPivotColumns;
            int lastColumn;
            int smallestBasicIndex;
            double quotient;
            IList<int> possibleRows = new List<int>();

            // Initialize the output parameters to error values.
            row = -1;
            column = -1;

            // Get the column of the pivot element. This is the first cost column
            // with negative value and if there are more than one of such, the one
            // with smallest index. Note, that we have to check all columns except
            // for the last one containing the values initially given by the vector b.
            loop = 0;
            numberOfPivotColumns = tableau.GetLength(1) - 1;
            while ((tableau[0, loop] + LinearProgramming.Epsilon >= 0)
                && (numberOfPivotColumns > loop))
            {
                loop++;
            }
            column = loop;

            // If the column is equal or less than the number of pivot columns,
            // we can stop, as there is no pivot left.
            if (numberOfPivotColumns <= column)
            {
                row = tableau.GetLength(0);
                column = tableau.GetLength(1);
            }
            else
            {
                // Get the row of the pivot element. This is the one with smallest quotient
                // of b(i)/a(i, j) and a(i, j) > 0, and if there are more than one of such,
                // take the one with smallest column index if there are several pivot rows
                // fulfilling the conditions, where b(i) denotes the element of the
                // vector b and a(i, j) an element of the defining matrix.
                loop = 1;
                numberOfPivotRows = tableau.GetLength(0);
                lastColumn = tableau.GetLength(1) - 1;
                quotient = double.MaxValue;
                while (numberOfPivotRows > loop)
                {
                    // Check next entry in column for being pivot element.
                    if (0 < tableau[loop, column])
                    {
                        // Check if possible new pivot element fulfills the condition
                        // for being less than the quotient of the current pivot element.
                        if ((tableau[loop, lastColumn] / tableau[loop, column]) < quotient)
                        {
                            quotient = (tableau[loop, lastColumn] / tableau[loop, column]);
                            possibleRows.Clear();
                            possibleRows.Add(loop);
                        }
                        else if (Math.Abs(tableau[loop, lastColumn] / tableau[loop, column]
                            - quotient) < LinearProgramming.Epsilon)
                        {
                            // This case is not likely, but must be checked, just in case!
                            // It is basically a test for equality but with respect to epsilon.
                            possibleRows.Add(loop);
                        }
                        // Nothing to be done in the else case.
                    }

                    // Increment loop variable.
                    loop++;
                }
                // Now, we have the possible pivot rows. If there is only one of such,
                // this is the pivot row. Otherwise, we have to take the one with the smallest
                // assoicated column index as given by the list of currently valid basic indices.
                if (possibleRows.Any())
                {
                    if (1 == possibleRows.Count)
                    {
                        row = possibleRows[0];
                    }
                    else
                    {
                        loop = 1;
                        smallestBasicIndex = tableau.GetLength(1);
                        while (possibleRows.Count > loop)
                        {
                            // Get the row index with smallest column index, i.e. smallest
                            // basic index. Be aware, that the row index must be subtract by
                            // one for accessing the zero-based array of basic indices, as the
                            // first row in the tableau is the cost row and our row index has
                            // a valid range from 1 to 5.
                            if (smallestBasicIndex > basicIndices[possibleRows[loop]-1])
                            {
                                row = possibleRows[loop];
                                smallestBasicIndex = basicIndices[possibleRows[loop]-1];
                            }

                            // Increment loop variable.
                            loop++;
                        }
                    }
                }

                // As last step, check if the pivot row is still -1 and if so, set it
                // to the number of rows in the tableau. Also reset the column index to
                // the number of columns in the tableau. This means, there is no ohter pivot left.
                if (0 > row)
                {
                    row = tableau.GetLength(0);
                    column = tableau.GetLength(1);
                }
            }
        }

        #endregion // Public Static Methods (4)
    }
}

性能

关于性能，我个人没有数字来比较此算法与其他解决凸多面体碰撞检测问题的算法。因此，我唯一能说明的是一些基于单纯形法的一般性结果，因此也可以在相关文献或例如这里 https://mathworld.net.cn/SimplexMethod.html 中找到。

单纯形法本身通常是一种具有指数性能的方法，即

$O(exp(k))$

其中 $k \in \mathbb{N}$ 表示定义优化问题约束的线性系统的方程数。幸运的是，在实践中，对于一些定义明确的情况，单纯形法表现出线性性能，并且也可以证明这一点。因此，如果没有构建非常特殊的情况，可以认为本文介绍的碰撞检测算法将以

$O(k)$

来解决问题。尽管如此，这意味着应该限制单纯形法实现中迭代的次数，以避免在遇到麻烦时破坏性能。

备注

作为本文纯内容部分的最后一部分，有几件事需要提及，因为在决定是否使用此算法时必须考虑这些。

首先是性能问题。如前所述，在实际应用中，性能应该是线性的，因此相当不错。尽管如此，不能排除指数行为。此外，还存在更快的，但更粗略的碰撞检测方法，尤其是在相关多面体相距较远时。因此，如果用于碰撞检测系统，应该首先进行例如基于多面体包围盒或包围球的碰撞检测。如果这些测试暗示碰撞，则应使用更精确的改进测试，例如此处描述的测试。

给定算法执行理论上精确的凸多面体碰撞检测测试的一个优点是，您不需要多面体的特定形式或方向信息。多面体的顶点包含了该算法所需的所有信息。

如已暗示的那样，该算法仅在理论上是精确的。这意味着什么很容易理解。由于计算机在执行浮点数计算时的不准确性，需要一个有意义的停止标准来区分浮点数，即必须就区分两个浮点数的精度做出具体决定。例如，精度为 0.001 可能就足够了，因此，如果单纯形法返回的最小值为 0.001 以下，而不是正好为 0，则假定发生碰撞。

由于数值不准确性而可能出现的另一个问题是无限循环而没有进展。单纯形法的糟糕实现可能导致计算表格中的循环。理论上，可以通过使用专门的选主元算法来选择下一个单纯形法步骤中的主元来避免这些循环。例如，在此处编写的实现中，使用了 Bland 规则（https://en.wikipedia.org/wiki/Bland's_rule），该规则已被证明不会导致循环。不幸的是，由于数值不准确性导致的表格中的数字擦除，即使使用了可以证明无循环计算的主元选择算法，也可能导致循环。

在这里还必须强调的是，所介绍的算法可以判断多面体之间是否存在碰撞。它不计算两个多面体之间的距离。问题 $P2$ 中要最小化的函数仅提供（如前所述）向量 $b-Ax \in \mathbb{R}^{k}$ 的 1-范数。幸运的是，这至少可以让我们对两个多面体之间的距离进行或多或少精确的估计。如果两个多面体发生碰撞，距离显然为 $0$，如上所示。如果两个多面体不发生碰撞，则计算出的最小值 $>0$ 告诉我们，对于所有满足问题 $P2$ 约束的其他向量 $\tilde{y} := b - A\tilde{x}\in \mathbb{R}^{k}$，我们有

$\| \tilde{y} \| _1 \geq min f _{A} (x)$

这尤其适用于这类向量 $\tilde{y} \in \mathbb{R}^{k}$：

$\tilde{y} = \left(\begin{array}{lf} y \\ 0 \\ 0 \end{array}\right) \quad y \in \mathbb{R}^{n}$

其中，由于向量 $\tilde{y}$ 的最后两个元素为 $0$，并且满足属于两个凸多面体闵可夫斯基差的方程，因此有 $y \in (K-L)$。因此，如果计算出的最小值 $>0$，则对于所有此类 $y \in (K-L)$，它们的 1-范数大于或等于最小值。

如所述，这种估计的准确性或多或少，取决于给定的具体多面体。此外，您永远不会得到大于 $2$ 的最小值，因为您从 $x=0$ 开始使用单纯形法进行计算，只执行不使结果变坏的步骤，并且

$\| b-Ax \| _1 = \| b-0 \| _1 = \| b \| _1 = 2$

另一个问题是估计基于 1-范数。通常，实空间中的距离是使用欧几里得范数或 2-范数测量的，因为它直观地符合我们对现实世界的感知。由于我们只处理有限维实空间，现在我们可以使用范数等价性来估计以 2-范数测量的距离（有关更多详细信息，请参阅例如 https://en.wikipedia.org/wiki/Lp_space#The_p-norm_in_finite_dimensions）。对于任何 $z \in \mathbb{R}^{k}$，我们有

$ \sqrt{k} \| z \| _2 \geq \| z \| _1 \geq \| z \| _2$

这导致了以下结果，用于估计 $K$ 和 $L$ 之间在 2-范数下的距离——基于定义 $dist$ 函数的度量是 1-范数诱导的度量——通过重写不等式（在两个多面体不碰撞的情况下）并使用一个称为 $x^{\ast}$ 的优化问题的解

$ dist(K,L) \geq \| (b-Ax^{\ast}) \| _1 \geq \| (b-Ax^{\ast}) \| _2 \geq \frac{1}{\sqrt{n}} \| (b-Ax^{\ast}) \| _1 > 0$

因此，您可以通过仅使用计算出的最小值（参见上面的倒数第二条不等式）直接估计 2-范数下的距离，并将其用作多面体距离的估计值。另请注意，通过将 $k$ 替换为值 $n=k-2$ 来调整 $k$。这是因为对于 $K-L$ 中的所有可能点，结果最小向量的最后两个元素必须为 $0$，并且在这种有定义且给定的 1-范数值的情况下，此类向量的 2-范数的最小值由值在第一个 $n=k-2$ 元素上的均匀分布给出，即由向量

$z = \left(\begin{array}{lf} z _1 \\ \vdots \\ z _n \\ 0 \\ 0 \end{array}\right) \quad z _i := \frac{1}{n} \| (b-Ax^{\ast}) \| _1 , \, \, \forall i=1, \cdots, n$

不幸的是，这个值取决于相关实空间的维度 $n$。将单纯形法的实现修改为不仅返回计算出的最小值，还返回确定的 $x^{\ast}$ 本身，是无济于事的（如先前在此处所述，这是错误的）。这是因为 $x^{\ast}$ 不必是唯一的，因此，结果的最小向量及其 2-范数不能保证是（可能存在的）解中具有最小值的向量。

关于此处编写的实现，应指出它使用了标准的单纯形法，但存在一个修正的单纯形法，它等同于标准单纯形法，并且在计算方面更有效。有关更多信息，请参阅例如 https://en.wikipedia.org/wiki/Revised_simplex_method。

除了到目前为止所说的一切之外，我想对 Gilbert–Johnson–Keerthi 距离算法（例如，参见 https://en.wikipedia.org/wiki/Gilbert-Johnson-Keerthi_distance_algorithm）发表评论，因为这可能很重要。感谢 Kenneth Haugland 在评论中提到这一点。

如果您看一下 Gilbert–Johnson–Keerthi 距离算法，您会发现它在以下方面更好：它不仅提供碰撞结果，而且在没有碰撞的情况下，它还提供 2-范数下的距离，这通常比上面的方法更好。此外，Gilbert–Johnson–Keerthi 距离算法在特定情况下（经过适当实现）也具有近乎恒定的线性性能。它也是一个与本文提出的算法不同的算法，但确实是两者都使用了相同的集合计算概念，即闵可夫斯基差。我个人认为，由于 Gilbert–Johnson–Keerthi 距离算法还需要一些所谓的支撑函数来进行计算，因此本文介绍的算法更容易理解和实现，因为它仅依赖于多面体的顶点。因此，我希望它能为对碰撞检测感兴趣的人们提供一个良好的起点。

最后一点是关于使用单纯形法进行碰撞检测。这也并非全新的想法。参考 Christer Ericson 的《实时碰撞检测》（Real-Time Collision Detection by Christer Ericson），第 9 章（请注意，我引用的是网页，这本书很容易找到并购买）可以看到这个想法已经存在一段时间了。但是，与该书不同的是，本文使用的算法不是基于半空间而是基于多面体的顶点，导致使用单纯形法求解的方程组完全不同。

参考文献

这里列出的参考文献按在文章中出现的顺序分组。我想感谢 KIT - 卡尔斯鲁厄理工学院（前德国卡尔斯鲁厄大学）的 Andreas Kirsch 教授博士，因为本文介绍的算法代码基于他在 2005 年夏季学期在卡尔斯鲁厄讲授的“优化理论”课程讲义。我也要感谢 John Jiyang Hou 的文章，他实际上促使我花时间写这篇文章，以及 Kenneth Haugland 在下面的评论，他让我至少对 Gilbert–Johnson–Keerthi 距离算法以及 Christer Ericson 的实时碰撞检测书籍发表评论。

Code Project

https://codeproject.org.cn/Articles/1065730/Point-Inside-Convex-Polygon-in-Cplusplus

Wikipedia

Mathworld Wolfram

https://mathworld.net.cn/SimplexMethod.html

Christer Ericson

http://realtimecollisiondetection.net

KIT - Karlsruher Institute of Technology (former University of Karlsruhe (TH), Germany)

http://www.math.kit.edu/ianmip/~kirsch/en

历史

请在下方找到文章的历史记录。顺序从最新到最旧。

2016年6月7日：关于距离估计和Gilbert–Johnson–Keerthi距离算法的重要变更

修改了备注部分，以删除关于 2-范数下距离估计的错误陈述
在备注部分添加了信息，以改进 1-范数下的距离估计
在备注部分添加了关于 Gilbert–Johnson–Keerthi 距离算法的信息
更新了参考文献部分以反映最新更改

2016年6月5日：小改动

修复了备注部分方程中丢失了一个操作的错误。

2016年6月2日：小改动

修复了发现的拼写错误和错别字

2016年5月21日：小改动

调整了 ConvexPolyhedron 类型的实例初始化
根据代码更改更新了代码文件和程序
尝试修复设置的标签

2016年5月20日：进行了少量修复

修复了发现的错别字
调整了 ConvexPolyhedron.cs 中 Corners 属性的误导性注释
通过使用最小解 $x^{\ast}$ 澄清了备注部分中的距离估计
移除了 VS2013 标签，因为代码中使用了 C#6.0
由于我目前正在排查我的开发 PC，代码文件未调整，程序未重新编译，仅因注释的更改

2016年5月20日：初始版本日期

初始版本发布日期