65.9K
CodeProject 正在变化。 阅读更多。
Home

2D 折线顶点平滑

veen_rp
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.89/5 (29投票s)

2016 年 4 月 17 日

CPOL

8分钟阅读

viewsIcon

61379

downloadIcon

1368

通过插值（Catmull-Rom）或逼近（Chaikin）平滑 2D 折线

注意: 本文的 VB.NET 代码已由 GitHub 上的 xtos (Chris C) 移植到 C#，请参阅 PolylineSmoothCSharp，感谢 Chris。

简介与背景

在处理地图 (GIS) 或图表数据时，您会遇到 2D 点、线、折线和多边形等对象。这些对象有很多不同的名称：形状、路径、区域、区域等。在本文中，我将一个点视为单个 x,y 对或顶点，或者简单地称为 P；一条线视为一对顶点，其起点为 P1，终点为 P2；一条折线视为多个顶点集合，从 P1 到 Pn，其中 n > 2。在折线中，顶点按照其在集合中出现的顺序连接。多边形本质上是一条折线，其中起点连接到终点，即一条闭合的折线。有关图形说明，请参见下图。

在绘制这些对象时，通常需要平滑折线的顶点。我意识到 GDI 提供了 DrawCurve 和 DrawBezier 方法，但本文将更深入地探讨平滑折线的生成，并展示如何处理多于固定数量的顶点（在 DrawBezier 的情况下是 4 个顶点），以及如何调整“平滑度”。

折线平滑有两种方法：(a) 插值，这意味着原始折线点保持不变，在新平滑的折线中也会保留；(b) 近似，这意味着新平滑的折线将近似旧折线，但原始点不会被保留。第一种方法也称为卡尔丹样条或标准样条，第二种方法通常用二次或三次贝塞尔曲线来解决。同样，请参见下图以获得图形说明。

网上有很多关于样条、贝塞尔曲线等的信息。显而易见的起点是：维基百科上的样条，以及我特别喜欢的博客：Martin Doms 的《样条与曲线第一部分 – 贝塞尔曲线》。在 CodeProject 上，有一篇出色的深度文章：Kenneth Haugland 的《样条插值 - 历史、理论与实现》（顺便说一句，我是他所说的懒惰程序员的典型代表）。样条和贝塞尔曲线非常强大，因为它们是参数化的：它们表现得像数学函数，可用于估计、逼近或插值原始数据点之间的中间数据点。事实上，它们可以作为例如数据点的线性或多项式回归的替代方法。

然而，在为绘图目的平滑折线时，您不一定对底层函数感兴趣，而更关心性能和易用性。使用样条还有一个缺点，即您一次使用 3 或 4 个控制点或顶点，以分段的方式进行。如果想将其应用于整系列点，您必须以某种方式将各个曲线连接起来。这可以做到，也已经完成了，但很容易变得复杂。

本文将展示使用一种简单的样条进行插值，称为 Catmull-Rom 样条，以及一种非样条计算，用于近似，由 Chaikin 发明，称为 Chaikin 或 CornerCutting 算法。有关后一种方法的非常易读的文章，请参阅 Kenneth I. Joy 的 《Chaikin 的曲线算法》。

代码

首先，拥有一个具有 X 和 Y As Double 的 Point 类，并为该类定义标准的数学运算符，以便能够编写 PointC = PointA * PointB，这会很方便。这是我的 PointD 类

Public Class PointD
    
    Public Sub New()
    End Sub
    
    Public Sub New(nx As Double, ny As Double)
        X = nx
        Y = ny
    End Sub
    
    Public Sub New(p As PointD)
        X = p.X
        Y = p.Y
    End Sub
    
    Public X As Double = 0
    Public Y As Double = 0
    
    Public Shared Operator +(p1 As PointD, p2 As PointD) As PointD
        Return New PointD(p1.X+p2.X,p1.Y+p2.Y)
    End Operator
    
    Public Shared Operator +(p As PointD, d As Double) As PointD
        Return New PointD(p.X+d,p.Y+d)
    End Operator
    
    Public Shared Operator +(d As Double, p As PointD) As PointD
        Return p+d
    End Operator
    
    'and similar operators for "-", "*" and "/"
    '...
    
End Class

完整的类在源文件中提供。其次，在处理折线绘制时，我更喜欢使用 System.Windows.Forms.DataVisualization 命名空间中的 Chart Windows Forms 控件，该控件自 .NET 4 起已内置。所有这些都在提供的项目源代码中设置好了。

1. Catmull-Rom 插值

网上有很多关于编写 Catmull-Rom 样条的例子，例如上面我引用的 Kenneth Haugland 在 CodeProject 上的文章。我从 Nice Curves! 中获取了代码并进行了改编。

Private Function getSplineInterpolationCatmullRom_
(points As List(Of PointD), nrOfInterpolatedPoints As Integer) As List(Of PointD)
    Try
        'The Catmull-Rom Spline, requires at least 4 points so it is possible
        'to extrapolate from 3 points, but not from 2. you would get a straight line anyway
        If points.Count < 3 Then Throw New Exception_
                            ("Catmull-Rom Spline requires at least 3 points")
        
        'could throw an error on the following, but it is easily fixed implicitly
        If nrOfInterpolatedPoints < 1 Then nrOfInterpolatedPoints = 1
        
        'part1 
        'create a new pointlist to do splining on
        'if you don't do this, the original pointlist gets extended 
        'with the exptrapolated points
        Dim spoints As New List(Of PointD)
        For Each p As PointD In points
            spoints.Add(New PointD(p))
        Next
        
        'always extrapolate the first and last point out
        Dim dx As Double = spoints(1).X-spoints(0).X
        Dim dy As Double = spoints(1).Y-spoints(0).Y
        spoints.Insert(0,New PointD(spoints(0).X-dx,spoints(0).Y-dy))
        dx = spoints(spoints.Count-1).X-spoints(spoints.Count-2).X
        dy = spoints(spoints.Count-1).Y-spoints(spoints.Count-2).Y
        spoints.Insert(spoints.Count, _
            New PointD(spoints(spoints.Count-1).X+dx,spoints(spoints.Count-1).Y+dy))
        
        'part2
        'Note the nrOfInterpolatedPoints acts as a kind of tension factor 
        'between 0 and 1 because
        'it is normalised to 1/nrOfInterpolatedPoints.
        Dim t As Double = 0
        Dim spoint As PointD
        Dim spline As New List(Of PointD)
        
        For i As Integer = 0 To spoints.Count-4
            spoint = New PointD()
            For intp As Integer = 0 To nrOfInterpolatedPoints-1
                'define t as a fraction between point 2 and 3 based on the nr of
                'interpolated points desired
                t = 1/nrOfInterpolatedPoints*intp
                
                spoint = 0.5*( _
                    2 * spoints(i+1) + (-1 * spoints(i) + spoints(i+2)) * t + _
                    (2 * spoints(i) - 5 * spoints(i+1) + _
                                      4 * spoints(i+2) - spoints(i+3)) * t^2 + _
                    (-1 * spoints(i) + 3 * spoints(i+1) - _
                                       3 * spoints(i+2) + spoints(i+3)) * t^3)
                
                spline.Add(New PointD(spoint))
            Next
            
        Next
        
        'part3
        'add the last point, but skip the interpolated last point, so second last...
        spline.Add(spoints(spoints.Count-2))
        Return spline
    Catch exc As Exception
        'Debug.Print(exc.ToString)
        Return Nothing
    End Try
End Function

我所做的改编是

  1. 请参见上面代码部分的 part1：在遍历折线顶点进行插值平滑之前，我创建了一个从折线 P1 到 P0 的外插，并将其插入到原始点列表的副本（即 spoints As New List(Of PointD)）的开头。然后，将一个从 Pn 到 Pn+1 的类似外插插入到 spoints 的末尾。我这样做的原因是，Catmull-Rom 样条通过从原始折线中选取 4 个点作为分段，来计算样条上 P2 和 P3 之间的点 Pt。通过对外插原始折线的第一个和最后一个点，我可以在平滑插值输出中保留这些点。
  2. 请参见上面代码部分的 part2：实际计算的 Pt 的数量取决于所需的插值点数量。t 是 P2 和 P3 之间的一个归一化距离，其坐标由样条函数计算。因此，外层的 For Next 循环遍历 spoints，一次选取 4 个点，内层的 For Next 循环以 t = 1/nrOfInterpolatedPoints*intp 的距离计算 P2 和 P3 之间的插值点，其中 P2 和 P3 是从 spoints 定义的折线中取出的当前 4 个点。例如：如果需要计算折线 P2 和 P3 之间的 3 个插值点，我将生成 t = 1/3*0 = 0、1/3*1 = 0.3333 和 1/3*2 = 0.6667 的距离，计算新点 spoint 并将其添加到新点列表 spline 的末尾（我承认 nrOfInterpolatedPoints 实际上应该称为 nrOfInterpolatedSegments）。请注意，输入参数充当一种平滑度等级：在两个原始顶点之间插值越多，线段就越平滑。然而，这会达到一个最优值，超过该最优值后，折线的平滑度将不再受到影响。

在代码部分的 part3 中的最后一步是将最后一个点添加到新的 spline 点列表中。请注意，这是 spoints 点列表的倒数第二个点（或 spoints.Count-2）点，因为我们不想添加 part1 中外插的最后一个点。下面两张图展示了具有不同数量插值点的 Catmull-Rom 样条的示例。

2. Chaikin

有时您不希望对折线中的顶点进行插值，因为它们可能嘈杂、锯齿状、抖动或包含一些奇怪的异常值。在这种情况下，就需要进行近似。当然，您可以使用样条近似，但还有一种更简单、是的，更不具数学性的方法，称为 Corner Cutting。从 Kenneth I. Joy 上面提供的参考文章中，有以下图示。

对于折线的每个线段，您定义一个新的线段，其起点距离为 1/4，距离为 3/4（或距离终点 (1-1/4)）。如果迭代几次，您的折线将在原始点之间平滑地近似。简单而优雅。但有几点需要注意：(a) 该方法不是参数化的，意味着您无法连续计算新平滑折线上的每个点；(b) 起点和终点 P0 和 P4 会从新折线中被剪切掉。这部分代码相对简单，而且我也做了一些改编。

Private Function getCurveSmoothingChaikin(points As List(Of PointD), _
        tension As Double, nrOfIterations As Integer) As List(Of PointD)
    'checks
    If points Is Nothing OrElse points.Count < 3 Then Return Nothing
    
    If nrOfIterations < 1 Then nrOfIterations = 1
    
    If tension < 0 Then
        tension = 0
    ElseIf tension > 1
        tension = 1
    End If
    
    'the tension factor defines a scale between corner cutting distance in segment half length,
    'i.e. between 0.05 and 0.45. The opposite corner will be cut by the inverse
    '(i.e. 1-cutting distance) to keep symmetry.
    'with a tension value of 0.5 this amounts to 0.25 = 1/4 and 0.75 = 3/4,
    'the original Chaikin values

    Dim cutdist As Double = 0.05 + (tension*0.4)
    
    'make a copy of the pointlist and iterate it
    Dim nl As New List(Of PointD)
    For i As Integer = 0 To points.Count-1
        nl.Add(New PointD(points(i)))
    Next
    
    For i As Integer = 1 To nrOfIterations
        nl = getSmootherChaikin(nl,cutdist)
    Next
    
    Return nl
End Function

Private Function getSmootherChaikin(points As List(Of PointD), cuttingDist As Double) _
        As List(Of PointD)
    Dim nl As New List(Of PointD)
    
    'always add the first point
    nl.Add(New PointD(points(0)))
    
    Dim q, r As PointD
    
    For i As Integer = 0 To points.Count-2
        q = (1-cuttingDist)*points(i) + cuttingDist*points(i+1)
        r = cuttingDist*points(i) + (1-cuttingDist)*points(i+1)
        nl.Add(q)
        nl.Add(r)
    Next
    
    'always add the last point
    nl.Add(New PointD(points(points.Count-1)))
    
    Return nl
End Function

我所做的改编是

  1. 代码包含包装器 getCurveSmoothingChaikin()，它定义了与角部的切割距离或 cutdist。在 Chaikin 算法中，这是在 0.25 和 0.75 的相对距离处。我已将其转换为介于 0 和 1 之间的张力因子，它定义了 0.05 到 0.45 的相对距离的 cutdist，方法是计算 0.05+(tension*0.4)，与之相对或互补的角部则为 1-cutdist。值为 t=0.5 时，得到原始 Chaikin 的切割距离 0.25。
  2. 2. 第二个改编是迭代方法 getSmootherChaikin()，在该方法中，我将折线的原始起点和终点添加到新的平滑折线中。

通过上述方法，可以控制结果折线的平滑度以及原始折线拐角的张力。下面 3 张图展示了具有不同迭代和张力的 Chaikin 近似示例。

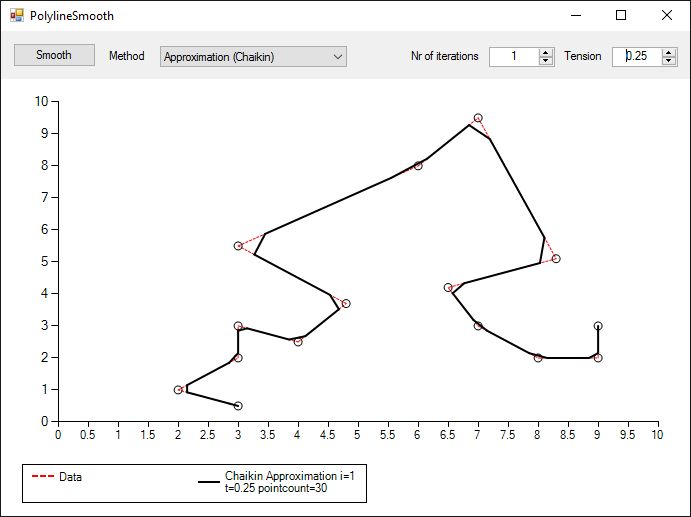
最后，下面 2 张图显示了两种方法对闭合折线（或多边形）的处理方式相似。请注意这里插值和近似的区别。敏锐的读者会注意到，闭合多边形中的起点和终点（即同一点）没有被平滑。您可以通过检查第一个点和最后一个点是否重叠来解决这个问题，如果它们重叠，则在复制点列表时，在该点周围插值一段线段。

Catmull-Rom 在闭合折线上的应用

Chaikin 在闭合折线上的应用

上述小型的 Windows 应用程序可以在提供的源文件中找到。

祝您编码愉快！

历史

  • 2016 年 4 月 17 日：文章撰写
  • 2019 年 4 月 2 日：添加了指向 GitHub 上本文 C# 移植版本的链接
© . All rights reserved.