双摆：一个 WPF 3D 模拟，用于检查双摆动力学

• 下载演示 - 166.4 KB
• 下载源代码 - 183.8 KB

引言

双摆是一个简单的物理系统，它表现出丰富的动力学行为，并且对初始条件非常敏感。在低能量下，运动是周期性的和准周期性的，随着能量的增加，运动变得越来越混沌。在非常高的能量下，混沌又会消失。

DoublePendulum 应用程序允许您通过两种不同的方式以图形方式指定初始条件，并在摆的 2D 和 3D 视图中显示由此产生的运动。为了研究长期行为，使用了庞加莱映射，它显示了系统在特定时间点的相空间状态。

背景

双摆的运动可以用称为经典力学的物理学领域来很好地描述。运动方程可以通过拉格朗日形式主义来求解。我在这里不打算解释这种形式主义，但您应该对机械系统的所谓相空间有所了解，所以让我们退一步，看看一个简单的摆。

简单的（平面）单摆

当我们从简单平面单摆的静止位置将其位移并释放时，它会以始终周期性的方式来回摆动。如果没有摩擦，它将一直以同样的方式运动直到永远。我们所说的摆是没有任何摩擦的纯粹数学系统。由于运动是平面的，我们可以使用二维坐标系来显示摆在特定时间的位置，如下图所示，来自维基百科。

最终，运动可以用一个关于角度 Θ 的标量方程来描述。由于杆的长度随时间恒定，因此可以从 Θ 计算出 x 和 y。

自由度与相空间

自由度是物理系统状态形式描述中的独立物理参数。在我们的例子中，角度 Θ 是一个独立的参数。事实证明，我们只需要第二个参数就可以完全描述一个简单摆的状态：角速度 ω。如果我们知道在某个特定时间 θ 和 ω，我们就可以计算所有时间的运动。

动力系统的相空间是表示系统中所有可能状态的空间，每个可能状态对应于相空间中的一个唯一点。随着时间的推移，动态系统从一个状态移动到另一个状态，这会导致相空间轨迹。

在我们的例子中，这个轨迹看起来非常简单。当角度 Θ 达到最大值时，角速度 ω 为 0。当摆向下移动到其平衡位置时，速度会增加并在 Θ = 0 处达到最大值。现在当摆向上移动到另一侧的最大角度（Θ < 0）时，速度会减小并在最大值（Θ = -Θmax）处变为 0。现在摆又开始向下移动，速度增加，但符号现在不同了。相空间中由此产生的轨迹是圆形的，如下图所示。

除了角速度 ω，还可以使用相应的角动量 L 来描述旋转系统的状态。在我们的例子中，角动量就是 r²*m*ω，其中 r 是杆的长度，m 是摆锤的质量（在模拟中两者都设为 1）。

恒定的总能量与自由度的损失

如前所述，角度和角速度（或动量）是简单摆的两个自由度。但是，如果运动中没有摩擦，系统的总能量就不会随时间变化。由于总能量是角度和速度的函数，如果我们知道其他一个以及总能量，我们就可以计算出另一个属性。这意味着无摩擦的摆会丢失一个自由度。

这也意味着相空间中的轨迹是二维空间的一维子集。在我们的例子中，是一个平面上的圆。

平面双摆

如果我们把第二个摆挂在第一个摆的末端，我们就得到了一个双摆。

这个系统的独立物理参数仍然是第一个质量的角度和角动量，但由于第二个质量可以独立移动，所以它的角度和角动量也是独立的参数。因此，双摆有四个自由度。

总能量现在是四个参数的函数，并且如果不存在摩擦，这个能量又会保持不变。因此，如果我们知道总能量，当我们知道其他三个参数时，我们就可以计算出这四个参数中的一个。因此，系统再次丢失了一个自由度，相空间轨迹是四维相空间的 ثلاثة维子集。

庞加莱映射

法国数学家和物理学家儒勒·亨利·庞加莱有一个伟大的想法，可以帮助我们可视化我们系统的长期行为。诀窍是通过将其中一个独立参数设置为特定值来从多维相空间中截取出某个部分，并检查系统何时穿过这个所谓的庞加莱截面。

例如，如果相空间是三维的，参数为 x、y 和 z，则该系统的轨迹将是在 3D 空间中的一条路径，比如我们现在坐着的房间。我们的系统可以是一个在房间里飞行的粒子。如果我们现在在我们房间的中间安装一个可渗透的平面，粒子会不时地穿过这个平面。每当发生这种情况时，我们在平面上的交叉点处做一个标记。

如果我们的粒子运动是非周期性的（或混沌的），它会在随机点穿过平面。即使它穿过一个已经被标记的点，它也可能以与之前完全不同的方向飞行。如果我们等待足够长的时间，我们的平面就会被标记完全覆盖。

但如果运动是周期性的呢？最简单的情况是粒子来回摆动。如果我们把我们的平面放在运动中间的某个地方，粒子总是会在同一点穿过这个平面。因此，平面上将只有一个标记。

如果运动稍微复杂一些，但仍然是周期性的，例如，如果粒子在圆周上飞行，则平面上将有两个标记（假设我们将平面放置在正确的位置）。现在如果我们考虑一个更复杂的（但仍然是周期性的）运动，最终在交叉平面上会有有限数量的标记。这是因为在某个时刻，我们粒子的运动会重复自身。

因此，系统的庞加莱映射可以让我们对动力学行为有一个直观的印象：简单的周期性行为将由映射中的几个点甚至一个点表示，而复杂的周期性行为则由许多但有限数量的点表示。混沌行为通过地图上随机分布的无限数量的点来揭示。

双摆的庞加莱条件

在之前的例子中，庞加莱映射是三维相空间中的一个二维平面，选择平面正确的位置和方向非常重要。如果我们把它放在系统永远不会穿过该平面的地方，那就没有什么帮助了。所以我们必须确定我们的双摆的四个参数（Θ1、L1、Θ2 或 L2）中哪一个适合构建庞加莱截面。我将使用角动量 L1 和 L2 而不是角速度 ω1 和 ω2。

如果摆在低能量下运动，Θ1 和 Θ2 都将取接近平衡值 Θ = 0 的值。即使在高能量下，当质量开始翻转时，其中一个角度是 0 的情况也会非常频繁地发生。所以让我们选择 Θ2 = 0。有了这个条件，我们可以将 4D 相空间减少到 3D 截面。

同样，由于总能量是恒定的，如果我们知道其中两个参数，我们就可以计算出剩余 3 个参数中的一个。因此，如果我们知道总能量 E0 和 Θ1 以及相应的 L1，我们就应该能够在 Θ2 为 0 的条件下计算 L2。结果表明，在大多数情况下，这个问题会有两个解：一个意味着下摆正在从其最低位置的左侧向右侧摆动，而它也可以从右侧向左侧摆动。

为了得到一个唯一的解，我们只需指定我们只接受下摆从其最低位置的左侧向右侧摆动的状态，这意味着它的角速度大于零。所以完整的庞加莱条件是 Θ2 = 0 且 ω2 > 0。

基于以上，我们可以使用二维图来表示我们在庞加莱条件下的 4D 系统的完整状态。该图在 x 轴上显示 Θ1，在 y 轴上显示 L1。现在，如果已知 E0，图上的一个点就对应于 L2，因为我们也知道对于该图上的所有点，Θ2 = 0 且 ω2 > 0。

理论够了！

让我们开始应用程序并四处看看。主窗口有三个视图：

• 摆的 3D 视图，显示实际运动（使用 WFTools3D 库创建）
• 摆的 2D 视图，用于设置初始值并显示实际运动
• 庞加莱映射，显示最近模拟的（Θ1, L1）值，也可用于开始新模拟

2D 视图允许您设置 Θ1 和 Θ2 以及 ω1 和 ω2 的初始值。您只需用鼠标左键拖动其中一个质量点即可。这样做时，3D 视图会相应更新。您还会注意到总能量 E0 会发生变化。能量不是以 SI 单位衡量的，而是以 m*g*l（m = 摆锤质量，l = 杆长度）为单位，这使得解释这些值很容易。

如果总能量为 0，则两个摆都处于最低位置且没有速度。值为 1 可能意味着其中一个质量被提高了 1 个单位长度。下图显示了不同能量下的双摆。

为了开始，让我们选择 Θ1 和 Θ2 的初始值，使总能量约为 0.01。将第一个质量点移动到其最低位置，第二个质量点稍微向左移动，如下所示。

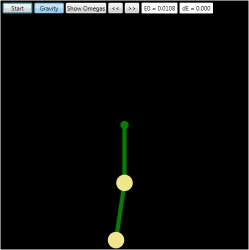
如果您现在通过单击“开始”按钮开始模拟，您可以在 2D 和 3D 视图中看到运动。每次系统通过庞加莱截面时，即下摆从其最低位置的左侧向右侧摆动时，2D 视图中的摆锤会闪烁红色，并且庞加莱映射中会添加一个新点。

事实上，您会注意到庞加莱图添加了两个点。这是因为我们系统的镜像对称性允许我们这样做。如果点 (Θ1, L1) 属于相空间中的一条轨迹，那么点 (-Θ1, L1) 属于一条密切相关的轨迹。它可能不是同一条轨迹，但为了更快地填充庞加莱映射，我也选择了添加第二个点。

片刻之后，庞加莱图将看起来像这样。

运动显然不是周期性的（这也可以在 2D 和 3D 视图中看到），但它也不是混沌的，因为这些点并不是随机分布在图中的，而是似乎形成了一个特定的形状。如果我们再等一会儿，地图看起来就会像这样。

我们现在可以通过单击“>>”按钮来加速模拟。大约一分钟后，应该会有很多点，它们之间（几乎）没有空白。

即使我们现在等更长时间，这个图像也不会改变。当然会添加新点，但它们会非常接近已有的点，以至于在视觉上没有区别。如果新点完全匹配现有点，则运动将从此开始重复。这意味着周期性运动。但在这种情况下，我们可以假设新点将添加到现有两点之间的某个位置，并且点在二维空间中形成一条曲线。这种行为称为准周期性，因为在某个时刻，两个点会如此接近，以至于我们从那时起无法看到运动中的差异。

添加另一条轨迹

通过单击“停止”按钮停止模拟。我们现在将添加另一条轨迹到庞加莱映射。为此，只需在现有曲线的上部上方某处单击鼠标右键，例如在此处显示的位置。

如果您释放鼠标按钮，新模拟将直接开始。现在添加到地图上的点将形成一条几乎与之前一样的曲线，只是有一个小的偏移。在模拟运行时，您可以单击其中一个颜色按钮来更改此模拟点的颜色。

选择接近另一组参数的初始系统参数会导致几乎相同的行为，这表明我们的系统是非混沌的。混沌意味着初始设置的微小变化会导致完全不同的行为。

添加更多轨迹

通过在庞加莱图上单击鼠标右键可以停止模拟。再次在最后一个曲线的正上方添加一个模拟，并将其颜色更改为其他颜色。结果可能看起来像这样。

这次，生成的曲线似乎形成了一个封闭的形状（以青色显示）。这是一件有趣的事情，因为这意味着无论何时选择形状内部的初始点，所有后续点也将位于该形状内部。否则，如果存在交叉点，系统将表现得像之前一样，这意味着所有后续点将位于先前轨迹形成的边界上。所以，让我们通过停止当前模拟并添加一个形状内部的新初始点来验证这一点。在我这边，结果看起来像这样。

而且，新的运动确实在之前的形状内形成了一个封闭的形状。显然，形状中间的运动有些特殊。所以停止模拟，并在右键单击的中间某个位置开始一个新的模拟。这是我的结果。

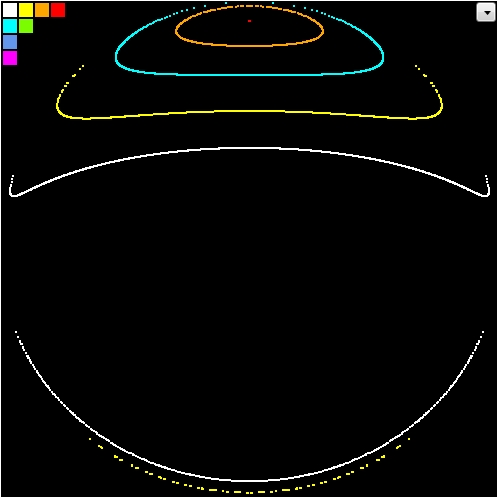
在同心曲线中间似乎是单个红点，实际上是许多非常接近的点。这意味着双摆现在正在以周期性的方式运动。如果您查看 2D 或 3D 视图，您会注意到两个摆实际上都在以相同的方式来回摆动。它们几乎完全同相摆动。

顺便说一下，如果您对当前模拟不满意并想删除这些点，只需停止模拟并执行 Ctrl+右键单击。我们现在可以用鼠标左键缩放到庞加莱图。只需在此处围绕中心点拖动一个矩形。

这表明运动不 strictly 是周期性的，但我们可以通过单击形状中心并再次放大结果来继续添加新的模拟。通过这种方式，我们将能够尽可能地接近奇异周期性运动。

但现在让我们通过将鼠标拖到左上角来缩小平移。如果您稍微移动鼠标，它将带您后退一步缩放，而大幅移动将带您回到整个画面。

现在让我们看看地图的下半部分。在第一个模拟的上方曲线下方添加一个新的模拟。它可能看起来像这样。

同样，庞加莱图中的点形成了一个封闭的形状（以蓝色显示），我们已经知道在这个形状的中心将存在另一个周期性运动。通过添加更多模拟，您可以轻松找到它。

虽然下同心曲线中心的红点可能在放大时显示为另一个曲线，但这表明摆至少非常接近周期轨道。查看 2D 和 3D 视图，您会发现两个摆都以几乎完全反相的方式运动。当上面的质量点向右移动时，下面的质量点向左移动，反之亦然。

低能量运动的总结

在低能量下运动时，只有两种周期性轨道：同相和反相振荡。这两种运动的阶数非常高：它们在庞加莱映射中的表示仅由一个点组成。所有其他运动都是准周期性的，并且是周期性轨道的一种卫星。

此外，值得再次提及的是，每当长期模拟的点形成一个封闭的形状时，我们都会在该形状的中间找到一个周期性运动。

更高能量下的双摆

以下部分描述了双摆在逐步提高能量时的行为。事实证明，开始时会出现新的周期性振荡，阶数会降低。阶数降低意味着该运动的庞加莱点数量会增加。所以运动仍然是周期性的，但更复杂。总而言之，相空间被准周期性运动所主导。

当总能量达到大约 0.8 时，发生了一些新的事情：一条显示准周期运动的曲线开始模糊。它显示为一个带状，而不是一条清晰的线，并且带的宽度随着能量的增加而增加。很快，该带状将占据相空间的很大一部分，这就是混沌的来源。

在能量为 4.5 时，所有周期性和准周期性振荡都消失了，所有运动都是混沌的。但很快，从能量 5 开始会出现新的周期性运动。现在摆有足够的能量进行旋转，并且对于大多数周期性运动，两个摆将以相同或相反的方向旋转。

在非常高的能量（> 1000）下，大多数周期性运动再次消失，准周期性运动主导了场景。最终，不再有混沌，所有运动都是准周期性的，并且只有一个周期性旋转。如果不存在重力，情况也会如此。

E0 = 0.1

与之前一样，存在两种周期性振荡（同相和反相），所有其他运动都是准周期性的。

E0 = 0.2

在同相区域出现了一种新的周期性运动，由绿色中的三个闭合曲线表示。

E0 = 0.25

在反相区域出现另一种新的周期性运动，由品红色中的四个闭合曲线表示。

E0 = 0.3

两个新周期性运动的影响区域在扩大。上方的曲线趋向于同相状态，而下方的曲线则远离反相状态。

E0 = 0.4

影响区域再次扩大。这些区域可以被视为中间周期性运动的吸引子。如果摆从吸引子内的位置开始，它将围绕相应的周期性运动波动。请注意，品红色吸引子完全包含在反相运动吸引子中。

E0 = 0.6

在此能量下，品红色吸引子离开黄色吸引子。正如您在下一张图片中看到的，两个吸引区域之间的状态变得有些随机，这可以通过白色点的较大带宽来体现。

E0 = 0.8

出现了两个新的吸引子：一个在同相区域，一个在反相区域。这两个吸引子的相应周期性运动具有周期性 5，即每 5 个点运动重复一次。

E0 = 1.0

这里发生了一些非常有趣的事情！同相和反相运动之间的区域分裂成许多不同的高周期性吸引子。两个品红色吸引子之间的带的展宽变大了。尽管系统尚未表现出混沌，但其运动正变得越来越复杂。

E0 = 1.2

混沌肯定已经进入系统。以前所有运动都与系统的周期性状态有关，但现在有一个区域，由青色的点可视化，它没有中心。如果摆从该区域内的某个点开始，下一个点可能会出现在同一区域内的任何地方。同样，如果您在紧邻的两个点开始两个模拟，它们的轨迹将很快发散。这种对初始条件的强烈敏感性是（确定性）混沌的主要标志。

E0 = 1.5

正如您可能已经预料到的，混沌运动的区域在增大，周期性运动的吸引子在变小。有趣的是，反相点分裂成两个点。

E0 = 1.9

大的反相吸引子完全分成两部分，其他吸引子再次变小，有些甚至消失了。

E0 = 2.3

现在，在能量增加时出现的所有吸引子都消失了，只剩下同相和反相吸引子。

但是一个新的吸引子也进入了系统，这是一个有趣的吸引子。请记住，当系统总能量为 2 时，下质量点恰好在上方质量点之上（但此时没有速度，否则总能量将大于 2）。由于现在总能量为 2.3，下质量点有足够的能量通过该上方位置。因此，出现了一种以前不存在的新运动：旋转。

事实上，如果您在新的吸引子（品红色）的中心开始模拟，当下摆完成一个旋转周期时，上摆完成一个振荡。

E0 = 2.9

新的旋转吸引子又消失了，同相和反相区域的吸引力也越来越小。混沌统治着世界，剩余的吸引子在混乱的海洋中显示为微小的岛屿。

E0 = 3.0

反相周期运动已被海洋吞没，只有同相吸引子在与汹涌的混沌波浪顽强搏斗。

E0 = 4.0

这又是一个有趣的情况。E0 = 4 意味着上质量点能够到达支点上方的点，但没有任何速度。所以它处于上摆也能开始旋转之前。尽管同相周期运动仍然稳定，但其吸引子再次变小。

您还会注意到相空间状态分布的整体形状正在发生变化。以前所有庞加莱点或多或少都包含在一个圆内，而现在 x 轴两端都有一个尖端。

请记住，庞加莱图的 x 轴显示上摆的角度。如前所述，该角度现在可以达到其最大值 180 度。y 轴显示角动量，当摆达到最大角度时，角动量必须为 0，否则能量将大于 4。虽然对于较低的能量，摆也表现出相同的行为，但在能量为 4 时，情况变得尤为突出。

E0 = 4.5

现在上摆也能够进行旋转了，混沌是世界唯一的统治者。即使是我们从一开始就陪伴着我们的勇敢的同相振荡，最终也沉入了波涛之下。不再有稳定的周期性运动。

请注意，在 x 轴的远端，当角度 Θ1 为 180 度时，现在有足够的能量来获得角动量 L1。这就是为什么在这些最大 x 值处，y 轴的正负两边都有点。

E0 = 5.0

看到曙光了！一个新吸引子从海中升起！但实际上它并非全新，而是在能量为 2.3 时出现过一次：那就是下摆完成一个旋转，而上摆完成一个振荡。令人惊讶的是，这种运动现在又出现了。

E0 = 8.0

绿色吸引子获得了更大的影响，并且出现了一个新的微小白色吸引子。请记住，我们摆的最大势能为 6。需要这个能量才能使两个质量点都移动到支点上方。现在总能量大于 6，摆可以到达这个位置并且仍然有足够的能量继续移动。这正是新的吸引子所发生的情况。两个摆以相同的频率但相反的方向旋转。这种运动在 2D 和 3D 视图中看起来很棒，而且令人惊讶的是它是稳定的！

E0 = 9.7

出现了更多的旋转吸引子。这次也在以前的同相区域。如果您在上面的白色吸引子处开始模拟，您将看到两个摆以相同的方向旋转。

您绝对应该尝试一下下面的红色和黄色吸引子！摆以不同的方向旋转，而在白色吸引子处频率相同，现在它们的比率分别是 1:2（红色）和 2:3（黄色）。由此产生的运动看起来非常棒！

E0 = 13

混沌被推回，出现了更多的吸引子。蓝色属于一个频率比为 1:3 的反相旋转。在同相区域，白色吸引子显示出一个有趣的图形。虽然上半部分属于严格拉伸的旋转，但另一个周期性运动分裂开来，下摆围绕拉伸的位置振荡。

E0 = 20

混沌区域再次变小，虽然没有新吸引子出现，但它们的影响力变大了。

E0 = 60

一些吸引子消失了，准周期性旋转占据了上风。混沌肯定在退潮。看看红色的上方吸引子！

E0 = 200

混沌完全消失了下反相区域，现在由准周期性运动控制。同相区域只剩下一个小混沌带。

E0 = 4000

在这个非常高的能量下，混沌消失了！除了拉伸旋转之外的所有吸引子都变小了。

E0 = 64000

现在总能量比之前大了 16 倍，或多或少只剩下一个周期性运动（占主导地位的白色吸引子）。红色和绿色吸引子的影响范围非常小，当能量进一步增大时，它们就会消失。

摘要

平面双摆的运动可以分为三类，其特征是系统的总能量

1. 当能量不足以进行旋转时，相空间被准周期性振荡所主导，有两种严格的周期性状态：同相和反相振荡。
2. 然后，当能量增大，但仍然不足以让两个摆轻松旋转时，首先出现新的周期性运动，很快就变成混沌。系统高度依赖于初始条件。
3. 一旦能量大于最大势能，就会出现周期性旋转。混沌退居次位，最终只剩下一个周期性旋转。所有其他状态都是准周期性的。

代码

让我从下往上给你一些关于这个相当简单的 WPF 应用程序代码的细节。这一节只涵盖了主要的类，我希望辅助类会自己说明。

类 PendulumData

这是代码的数学基础。该类持有双摆的四个初始状态参数，并通过一种数值积分方法“最后点近似”（LPA）来计算时间的进展。LPA 比龙格-库塔技术更容易使用，并且在误差方面对于我们的系统来说是可以接受的。

状态参数是 q1, q2, w1 和 w2，其中 q 代表角度，w（即 *omega*）代表角速度。要使用这些参数初始化数据模型，只需调用 Init(double q01, double q02, double w01, double w02)。此方法将计算相应的角动量 l1 和 l2 以及总能量 e0。

除了上面允许您以完全自由的方式选择摆的物理状态的 Init() 方法之外，还有另一个方法，当摆应该以庞加莱条件开始时使用。此方法的签名是 Init(double e00, double q01, double l01)，因此它获取总能量以及第一个质量的角度和角动量。由于庞加莱条件意味着 q2 = 0 且 w2 > 0，该方法现在可以通过求解二次方程来计算 l2，然后得到 w1 和 w2。

摆的运动由 Move(int numSteps) 方法计算。numSteps 参数允许调用方法检查模拟应该何时终止的条件，而不会过多地降低性能。它的值仅用于一个循环，该循环会重复执行给定次数的实际计算。

这个实际计算是最后点近似，工作方式如下：

1. 四个状态参数 q1, q2, w1 和 w2 导致两个质量的角加速度 a1 和 a2（通过拉格朗日力学）
2. 每个角加速度都会导致相应角速度的变化。如果我们选择一个足够小的时间间隔 dT，我们可以进行线性近似 w1 += a1 * dT（w2 也一样）。
3. 现在角速度本身会导致新的角度，我们也可以通过 q1 += w1 * dT（q2 也一样）来计算。
4. 有了这些新的状态参数，我们就可以回到第一步计算新的加速度。

时间间隔 dT 对于上述线性近似的有效性至关重要。如果我们选择得太大，系统将不会表现得“自然”，结果也将不正确。选择它非常小会减少误差，但会降低我们模拟的性能。所以需要有一些检查来告诉我们，在一定时间后模拟是否仍然有效。

事实证明，总能量允许我们进行此测试。如前所述，我们系统的总能量是恒定的，因此如果我们不时地计算总能量，我们可以将其与初始能量进行比较，如果差异足够小（例如 < 0.1%），我们可以假设模拟是好的。这在 Move() 方法的末尾完成。差异以百分比形式存储在变量 dE 中。

时间间隔在 Init() 方法之一中设置能量时重新计算。更高的能量需要更小的 dT 才能获得相同的相对误差。它的选择方式是，当能量为 1 时，dT 为 1e-6。

在计算新的状态参数之前，Move() 方法还会检查摆是否处于庞加莱条件。这不能通过直接测试 q2 是否等于 0 来完成，因为分步积分不会精确得到这个值。但是，如果我们将在集成之前将 q2 的值存储在变量 q2old 中，我们可以通过以下表达式识别庞加莱条件 (q2 = 0 且 w2 > 0)：(q2old < 0 && q2 >= 0 && q2 <= Math.PI / 2)。如果表达式为真，则发生两件事：

1. 进行线性插值以计算 q2 精确为 0 时的系统状态。此状态作为新的 PoincarePoint 存储在列表中。
2. 触发一个事件，通知观察者列表已添加新点（NewPoincarePoint）。

类 Simulator

此类具有 PendulumData 实例和用于启动和停止模拟的方法，模拟在其自己的线程中使用 BackgroundWorker 执行。这确保了 UI 在执行耗时的模拟时保持响应。

模拟本身在 Worker_DoWork() 方法的无限循环中完成。在该循环内，摆移动一千次，然后检查循环是否应该终止。使用计数器在 UI 中显示计算速度。

如果在 Move() 方法中检测到庞加莱条件，则会调用事件处理程序 Data_NewPoincarePoint()。此处理程序仅调用后台工作程序的 ReportProgress() 方法，该方法反过来调用 Worker_ProgressChanged() 处理程序。最后一个方法在 UI 线程中执行，而前面的方法在后台线程中执行。因此，我们可以在此方法中修改 UI 元素。

由于 Simulator 类不知道 UI 元素，它也只触发一个事件，该事件将在 UI 中处理。此事件的名称与 PendulumData 类中的事件名称相同：NewPoincarePoint。

类 PendulumModel2D

此 UI 元素显示摆的 2D 模型，并允许您修改模拟的初始参数。它只是一个 WPF Canvas，其中包含一些线条、曲线和圆圈，它们根据 Simulator 类中的 PendulumData 实例在 Update() 方法中定位和渲染。此数据模型本身不是一个实例，只是对 Simulator 类中实例的引用。

应注意的是，此 UI 元素不修改数据模型，而只是读取 Q1, Q2, W1, W2, A1 和 A2 的值来显示摆锤的位置、速度和加速度。

还有一个名为 NewPoincarePoint() 的方法，它会将下摆锤的颜色更改为红色 120 毫秒。当模拟期间庞加莱条件为真时会调用此方法。

类 PendulumModel3D

在现实世界中，有许多方法可以构建双摆，其中一种可能看起来像这个有趣的摆。我没有真正尝试过，但我猜它会起作用。

3D 模型是使用 WFTools3D 库创建的，您可以在 codeproject 和 github 上找到它。

此 UI 元素还包含对模拟器类数据模型的引用，它只是读取 Q1 和 Q2 以在 Update() 方法中显示摆的当前状态。

请注意，3D 视图是交互式的。您可以将相机移动到任何位置，甚至可以使用前面提到的文章中找到的键盘和鼠标命令在场景中飞行。

类 PoincareMap

该映射实现为一个 WPF Border，其中有一个 Image 作为子元素。此图像的 Source 设置为 WriteableBitmap 类的实例。

使用伟大的扩展库 WriteableBitmapEx 将点添加到位图，您可以在 此处 和 github 上找到它。

与 2D 和 3D 摆模型一样，映射从对模拟器数据模型的引用中读取当前模拟的数据。要向映射添加更多模拟，可以使用 CloneData() 方法。此方法复制当前数据模型并将其添加到内部列表中，该列表在 Redraw() 方法中进行渲染（与当前数据模型一起）。

缩放功能通过 PixelMapper 类实现，该类持有一个线性变换堆栈，用于将数据值映射到屏幕坐标。

类 MainView

这个 WPF UserControl 将所有内容整合在一起！它拥有一个模拟器以及所有用于控制模拟的视图模型、控件和事件处理程序。这使得将整个功能轻松添加到您自己的应用程序中。

类 MainWindow

这个 WPF Window 只是嵌入了一个 MainView 并负责应用程序窗口的定位。我讨厌那些不记住其最后位置的应用程序！

改进之处

如果您想自己研究双摆的长期行为，您需要永久存储模拟数据。此处提供的代码是我用于创建上面显示的庞加莱图的代码的一个子集。在一台计算机上创建这些图需要数天甚至数周的时间，所以您希望确保工作不会丢失，以防下次停电导致您的机器损坏。

您可以使用附加线程一次计算多个模拟来加快速度。现代计算机拥有 4、8 甚至 16 个 CPU，它们大部分时间都在休眠！当我 20 年前（！）开始这个项目时，情况有所不同，每台机器只有一个 CPU，而且多线程（至少对我来说 :-）几乎不为人知。幸运的是，我在一家软件公司工作，所以我能够做一些我称之为多机处理的事情。当我们的日常工作完成后，我在我能接触到的每台计算机上启动模拟。周末也是如此！

添加更多视图到数据也很有趣，例如，一个 3D 视图，显示相空间轨迹在 4D 空间的子集中。下图显示了一个相当复杂的周期性运动在 (Q2, L2, L1) 空间中的路径。白色曲线代表路径，另外两条是坐标平面的投影。

您还可以为庞加莱映射添加第三个维度。请记住，该图显示 L1 与 Q1 的关系，并且 L2 可以从总能量中计算出来。结果，3D 庞加莱点位于所谓的能量壳上，如下图所示。

结束

我希望您喜欢阅读这篇相当长的文章，就像我喜欢编写这个简单但非凡的动态系统的代码一样。如果您对我在模拟数据中收集到的数据感兴趣，请给我留言，我们将找到一种传输 65 MB 数据的方法。

祝您编码愉快！

历史

2016年5月5日：首次上传