CT（计算机断层扫描）- C# 中的正弦图图像生成

• 下载 MakeSinogramExe.zip - 9.7 KB
• 下载源代码 - 27.7 KB

1. 引言

在医学成像领域，计算机断层扫描（CT），有时也称为计算机轴向断层扫描（CAT），是一种重要的成像方式。这是结构成像的一部分，与核医学等功能成像方式相对。

本文描述了根据正在成像的切片的图像生成Sinogram图像。

在计算机断层扫描中，X射线束穿过感兴趣的解剖切片，并且产生的X射线被捕获在源的另一侧的探测器上。源-探测器组合绕成像物体旋转一整圈，以捕获大量的投影图像。这构成了CT的“图像采集”方面。

图像采集步骤之后是“重建”步骤，其中使用特殊的重建算法（如反投影和滤波反投影）来恢复成像切片的解剖细节。

上述CT问题可以从两个方面来看：

 

1. 前向问题：给定切片的解剖细节，计算投影图像。这是一个相对容易的问题，因为可以使用X射线衰减的标准规则来生成投影图像。给定一个图像切片，可以生成任意数量的投影图像；这些投影图像在投影角度上有所不同。投影图像是通过一个称为Radon变换的数学实体生成的。本文是关于使用Radon变换来生成图像的Sinogram。Sinogram是一个图像，我们提供了生成Sinogram的详细计算步骤。
2. 逆问题：给定投影图像，计算解剖切片的细节。这比前向问题要难得多，并且在其最基本的形式中涉及逆Radon变换。与所有逆问题一样，对于所有类型的输入，并不保证能够准确重建切片，特别是当存在缺失投影值等歧义时。逆问题的解决方案是我们后续文章的内容。

2. 问题数学简述

Radon变换与投影函数相关。投影是一组关于物体某个参数的积分测量值，这些积分沿着通过物体的直线进行。这些积分称为线积分。在CT的情况下，积分的参数是X射线衰减常数；这个X射线衰减常数在正在成像的解剖切片中是变化的，并且投影（对于特定角度）是该切片中该衰减常数分布的函数。

在本篇文章中，我们考虑的是平行束CT，而不是扇形束CT。下图取自Avinash Kak和Malcolm Slaney的《计算机断层成像原理》第三章，该书可免费下载 此处。从图中可以看出，两个不同角度θ₁和θ₂的投影是不同的。我们不提供方程，但上述书籍包含了所有必要的数学内容。

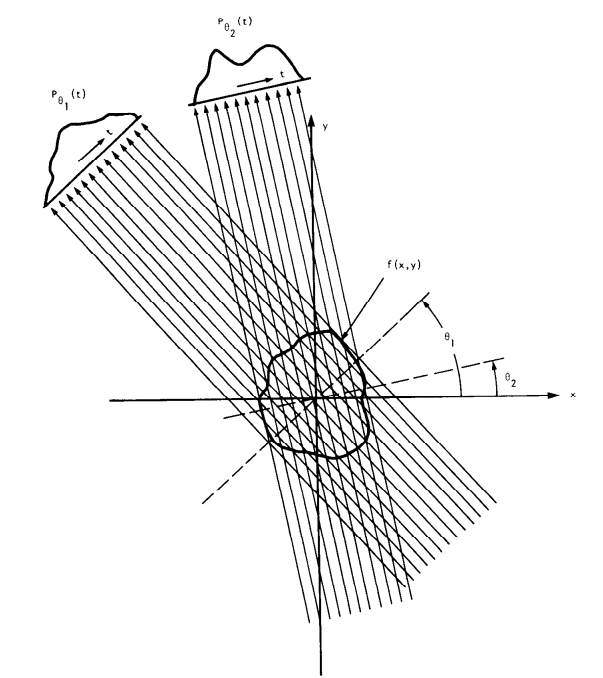
由于投影函数是一组强度，这些强度被描绘为入射角（incidence angle）的函数；由此产生的图称为Sinogram。在Sinogram中，通常，对应于0度角的投影强度显示为图像的最左侧垂直线。对应于1度角的投影强度显示为比0度线向右一个像素的垂直线。以此类推，直到将180条线并排累积，对应于0到180度的范围。有些人更喜欢显示直到360度的所有线条，但对于平行束CT，角度θ的投影强度是角度180 + θ的投影强度的镜像。在本篇文章中，我们使用180个投影。因此，在这种情况下，Sinogram图像的宽度始终为180。

如果输入切片是矩形的，通过在两侧适当填充像素，可以方便地将其转换为正方形。该软件程序会对矩形图像进行这样的像素填充，将其转换为正方形。

此软件应用程序允许您加载图像，计算图像的Sinogram，并允许您保存Sinogram图像。此外，它还允许您反转Sinogram。

3. 生成Sinogram的代码

生成sinogram的代码分为三个类，如下所述：

1. SquarePaddedImage.cs：此类负责通过在图像上适当填充暗色像素来将矩形图像转换为正方形图像。如果原始图像的宽度大于高度，则在图像的顶部和底部添加暗像素。另一方面，如果原始图像的宽度小于高度，则在图像的左侧和右侧添加暗像素。在顶部和底部或左侧和右侧添加像素的逻辑嵌入在ComputePaddedImage()函数中。例如，在顶部和底部填充像素的逻辑如下所示：

   if (originalWidth > originalHeight)
   {
   	// Width is greater than height; so we pad background pixels at the top and bottom
   	// of the image, so that the original image comes in the middle of the square block
   	PaddedWidth = originalWidth;
   	PaddedHeight = originalWidth;
   	InitializePaddedPixels();
   
   	int diff = (PaddedHeight - originalHeight) / 2;
   
   	for (int i = diff * PaddedWidth; i < diff * PaddedWidth + originalWidth * originalHeight; ++i)
   	{
   		Pixels8PaddedRed[i] = pixels8OriginalRed[i - diff * PaddedWidth];
   		Pixels8PaddedGreen[i] = pixels8OriginalGreen[i - diff * PaddedWidth];
   		Pixels8PaddedBlue[i] = pixels8OriginalBlue[i - diff * PaddedWidth];
   	}
   }
     

   此外，此类还读取原始图像，并能够从填充的图像创建位图。
2. ImageRotation.cs：此类负责将正方形图像按给定角度旋转。例如，如果旋转角度指定为3度，此类可以执行 such a rotation，并输出resulting pixel array。此外，它还可以输出resulting bitmap。

    

   通过旋转公式，然后进行双线性插值来实现正方形图像的旋转。通过改编自互联网上的代码实现了包含双线性插值的旋转代码。
3. Sinogram.cs：这是程序中最重要的类，它负责计算Sinogram图像。首先，将输入图像填充为正方形图像。然后，在一个循环中，将图像旋转一个角度，并将像素值累加到sum变量中。这些sum值都适当地放置在sinogramValues缓冲区中，然后用于生成Sinogram图像。下面给出了计算sinogramValues缓冲区的相关代码片段：

   // Populate the sinogram buffer
   for (int k = 0; k < numberOfAngles; ++k)
   {
   	angleDegrees = -k;
   	// Just watch the console for large images. 
   	// It should go on until 180.
   	Console.Write(k + " "); 
   	ir.RotateImage(angleDegrees);
   	pixels8RotatedRed = ir.Pixels8RotatedRed;
   	pixels8RotatedGreen = ir.Pixels8RotatedGreen;
   	pixels8RotatedBlue = ir.Pixels8RotatedBlue;
   
   	for (int i = 0; i < SquareWidth; ++i)
   	{
   		sum = 0;
   		index1 = i * numberOfAngles + k;
   		for (int j = 0; j < SquareHeight; ++j)
   		{
   			index2 = j * SquareWidth + i;
   			red = pixels8RotatedRed[index2];
   			green = pixels8RotatedGreen[index2];
   			blue = pixels8RotatedBlue[index2];
   			gray = red * 0.3 + green * 0.59 + blue * 0.11;
   			gray /= maxsum;
   			sum += gray;
   		}
   		sinogramValues[index1] = Math.Exp(-sum);
   	} 
   }  

4. 这三个文件，以及主窗口的XAML和CS文件，都打包在一个Visual Studio 2010解决方案中。

4. 验证

为了验证，我得到了我的学生的帮助，他们非常熟悉MATLAB软件并可以访问它。我们选择了一组代表性图像，在我们的程序和MATLAB中运行它们，以检查两个方面是否匹配良好：

• sinogram的形状，以及
• sinogram的强度。

用于创建Sinogram的MATLAB代码是：

I1 = imread('Fig1.png');
I = rgb2gray(I1);
theta = 0:180;
[R,xp] = radon(I,theta);
imagesc(theta,xp,R);
colormap(gray);

结果的表格如下所示：

原始图像	本程序生成的Sinogram	MATLAB生成的Sinogram

最后一个是众所周知的Shepp-Logan幻影。

可以看到，对于这组代表性图像，sinogram的形状与从MATLAB获得的形状非常匹配。这不包括两个sinogram的比例不同，因为MATLAB似乎使用了其特有的几何比例因子来缩放图像。

关于强度，您可能会注意到我们的一些代表性图像的sinogram之间存在明显的强度差异。这可能是由于我们的程序和MATLAB之间的强度缩放差异造成的。在我们的程序中，我们将sinogram的最大强度映射到255，最小强度映射到0。我们分别从最大值和最小值加减一个微小的epsilon（0.00001）值，以确保最大像素值不超过255，最小像素值不低于0。这种强度缩放可能在MATLAB中有所不同，这可以解释强度差异的原因。

5. 值得关注的要点

在这个程序中，我们并没有过多关注程序的性能，您可能会发现计算有点慢。我们的重点主要放在功能上。在Debug模式下运行此程序时，您可以在Debug输出窗口中看到角度值从0以1为步长递增到180的计数器。

如果需要计算Sinogram的感兴趣区域位于正方形图像的内接圆内，则会获得最佳结果。对于位于内接圆外的角落区域，有不同的处理方法，我们在此不进行任何特殊处理。

GUI中的Sinogram图像以填充模式显示，因此看起来不会被压扁。尽管其宽度始终为180像素。

通过更改Sinogram.cs文件中的numberOfAngles值，可以为360度而不是180度计算Sinogram。

我们将在后续文章中重点讨论重建方面。

6. 结语

本文介绍了一种给定图像计算Sinogram的方法。第一步是适当填充图像，将任何矩形图像转换为正方形图像。在接下来的两个步骤中创建Sinogram：（i）将正方形图像旋转特定角度，（ii）计算旋转图像对应像素值的总和；这些步骤在一个循环中执行。通过与MATLAB进行比较来验证生成的Sinogram。

希望本文能帮助大家理解Sinogram是如何从切片生成的。请尝试不仅为解剖图像，而且为任何通用图像生成Sinogram，并通过下面的评论区分享您的经验。如果您觉得Sinogram的计算有任何问题，请反馈。即使没有问题，也请提供您的宝贵评论。

历史

• 版本1.0：2016年7月19日。

致谢

感谢我的学生Atheeth P, Jagruthi A, Kishore KS, Lakshmi SD, Mamatha K, Savitha VS, Sutapa B，感谢他们耐心听我的讲座，并帮助我在MATLAB上运行我们的代表性图像，以及帮助我比较结果。