基于 Java 的量子计算库

引言

“任何不对量子理论感到震惊的人都没有真正理解它。” - 尼尔斯·玻尔。

量子计算机与传统计算机的不同之处在于它利用了量子力学效应，例如叠加，来进行计算。在传统计算机中，基本单位由一个只有0或1值的比特表示。与传统计算机相比，量子计算机的基本单位是量子比特（qubit），它通过利用叠加，可以同时表示0和1的值。

在本文中，我想介绍一个允许模拟量子算法的Java库。我编写这个库是因为我发现目前缺乏基于Java的模拟量子算法的库，现有的Java模拟器不导出API，也不能在项目中直接使用。 

背景

由于量子计算对读者来说可能不是一个熟悉的话题，在开始介绍使用该库实现的算法之前，我将对其进行简要介绍。在本章中，我将讨论复数、向量和量子比特。

 

复数

因为量子比特的概率幅是复数，所以我将从简要介绍复数背后的数学知识开始，然后介绍最基本的操作。

复数 q 定义为

其中 a 和 b 是实数， 是虚数单位。可以很容易地看出，复数有一个实部“a”和一个虚部“b*i”。通过改变复数虚部的符号，可以得到其复共轭。

通过改变复数虚部的符号，可以得到其复共轭。

现在，关于基本操作，我将介绍加法、乘法、模和复共轭的公式。

如果我们考虑两个复数 x 和 y，

这两个数的加法定义为

乘法定义为

是复数 x 的模，复共轭定义为

向量

在本小节中，我将简要介绍向量和线性代数。形式上，量子比特的状态是二维复向量空间 C² 中的一个单位向量。

向量 可以写成，其中 

这种列向量的表示法称为ket。相应的行向量称为bra。

内积 <v|v> 是bra-ket 或点积，是 bra 和 ket 向量之间的运算。

外积是ket-bra，其计算方式为

张量积的定义如下。如果 ，则张量积为

量子比特和门

量子力学告诉我们，任何这样的系统都可以存在于状态的叠加中。一般来说，一个量子比特的状态由下式描述： ，其中 a 和 b 是复数，满足 

在经典计算机中，AND 和 OR 等门操作构成了数据处理的核心；在量子计算机中，对量子比特也可以进行类似的操作。可以执行的门操作正是所有的酉线性操作。

一个重要的例子是哈达玛变换。它定义为

或者，如果我们考虑 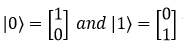 ，它可以表示为矩阵

哈达玛门创建了一个叠加态，通常在量子计算的开始阶段用于初始化数据处理，在结束阶段用于收集数据。

一组特别有用的单量子比特门是 Pauli 门，即 X 门、Y 门和 Z 门。

 

使用代码

在本章中，我将简要介绍量子计算库，并介绍 Deutsch 算法的实现。

库的简要描述

量子计算库包含了著名的门和基本量子比特的定义。此外，它还包含了所需的矩阵和向量运算的实现。

Qubit 类用于创建新的 Qubit 对象，并包含用于测试量子比特是否有效或两个量子比特是否相等的方。Qubit 类被子类继承，这些子类定义了“基本”量子比特 |0>、|1>、|+> 和 | ->。

/**
	 * Constructs a new <code>Qubit</code> object. 
	 * @param no0 complex number
	 * @param no1 complex number
	 * 
	 */
	public Qubit(ComplexNumber no0, ComplexNumber no1) {
		qubitVector = new ComplexNumber[2];
		qubitVector[0] = no0;
		qubitVector[1] = no1;
	}

	/**
	 * Constructs a new <code>Qubit</code> object.
	 * @param qubitVector an array of 2 complex numbers
	 */
	public Qubit(ComplexNumber[] qubitVector) {
		this.qubitVector =Arrays.copyOf(qubitVector, qubitVector.length);
	}

	/**
	 * Return the qubit represented as an array of 2 complex numbers.  
	 * @return qubit
	 */
	public ComplexNumber[] getQubit() {
		ComplexNumber[] copyOfQubitVector = qubitVector;
		return copyOfQubitVector;
	}

	/**
	 * Check if qubit state is valid
	 * @return true if the state is valid, otherwise false
	 */
	public boolean isValid(){
		double sum=0.0;
		for(ComplexNumber c:this.qubitVector){
			double mod=ComplexMath.mod(c);
			sum+=mod*mod;
		}
		return (sum==1.0);
	}

QubitOne |1> 和 QubitZero |0> 类定义如下。

public class QubitOne extends Qubit {

	/**
	 * Construct a new <code> QubitOne</code> object.
	 */
	public QubitOne() {
		super(new ComplexNumber(0.0, 0.0), new ComplexNumber(1.0, 0.0));
	}

}

public class QubitZero extends Qubit {

	/**
	 * Construct a new <code> QubitZero</code> object.
	 */
	public QubitZero() {
		super(new ComplexNumber(1.0, 0.0), new ComplexNumber(0.0, 0.0));
	}

}

库中使用抽象工厂模式实现门，要创建一个新的 Gate 对象，需要添加以下几行。

GatesAbstractFactory gateFactory = GateProducer.getGateFactory();
gateH = gateFactory.getGate(EGateTypes.E_HadamardGate);

目前，已实现的门有：

• 哈达玛门
• Pauli Z 门
• Pauli X 门
• C-Not 门

/**
 * Implemented Quantum Gates.
 * 
 *
 */
public enum EGateTypes {
	/**
	 * Hadamard Gate
	 */
	E_HadamardGate,
	/**
	 * Pauli-X Gate
	 */
	E_XGate,
	/**
	 * Pauli-Z Gate
	 */
	E_ZGate,
	/**
	 * CNOT Gate
	 */
	E_CNotGate
}

 

Deutsch 算法

我没有详细描述量子计算库中的每一行代码，而是选择展示一个著名且简单的量子算法的实现。在项目的存储库中也有 Grover 算法的实现，未来我将添加 Deutsch-Josza 和 Shor 算法。 

Deutsch 算法解决的问题在计算机科学中并非重要问题，但它是一个很好的例子，可以说明量子计算机如何被使用。这个问题可以通过量子计算机比传统计算机更快地解决，尽管不是指数级地快。

假设有一个函数 f，它接受1位输入/输出。

我们被要求判断这个函数是常函数还是平衡函数。这类函数的最大数量是4。

Deutsch 算法的量子电路图如下。

因此，我们需要实现的简单算法的步骤如下：

• 初始化
  • 创建 |0> (QubitZero) 对象；
  • 创建 X 门和 H 门对象。
  • 对定义哈达玛门的矩阵执行张量积；
• 算法
  • 将 X 门应用于第二个量子比特 0。我们称产生的量子比特为result。
  • 纠缠 |0> 和 result 量子比特。
  • 应用哈达玛门。
  • 应用 Oracle。
• 测量

//Initialization
gateH = gateFactory.getGate(EGateTypes.E_HadamardGate);
		gateX = gateFactory.getGate(EGateTypes.E_XGate);
		gateHH = MatrixOperations.tensorProduct(gateH.getUnitaryMatrix(), gateH.getUnitaryMatrix());

//Running the algorithm
resultQubit = QuantumOperations.applyGate(QuantumOperations.applyGate(
				QuantumOperations.applyGate(
						QuantumOperations.entangle(QUBIT_0, QuantumOperations.applyGate(QUBIT_0, gateX)), gateHH),
				oracle), gateHH);

//Measurement
measurementResults = new double[resultQubit.getQubit().length];
int i = 0;
for (ComplexNumber c : resultQubit.getQubit()) {
	measurementResults[i++] = Math.round(ComplexMath.multiply(c, ComplexMath.conjugate(c)).getReal());
}

//Helping method to test if a function is constant or not
public boolean isFunctionConstant() {
		int i = 0;
		ComplexNumber[] q01 = QuantumOperations.entangle(QUBIT_0, QUBIT_1).getQubit();
		for (ComplexNumber c : q01) {
			if (Double.compare(Math.round(ComplexMath.multiply(c, ComplexMath.conjugate(c)).getReal()),
					measurementResults[i++]) != 0) {
				return false;
			}
		}
		return true;

	}

 

关注点

关于这个项目，我只能说它带给了我很多乐趣，也让我学到了很多。同时，像任何新事物一样，它也带来了一些挫败感，但总体来说很有趣。我觉得量子计算这个主题很有意思，我开始阅读相关的课程和文章，理解了其中的数学和“魔法”，编写这个库是一个很好的练习，需要应用我学到的所有新知识。

关于该库未来的改进，我需要实现一个系统来更好地处理异常，并且我计划使用 C++ 和 JNI 来提高性能。

 

该项目的存储库可以在 这里找到。

 

历史

•  文章添加
• 更新了引言
• 添加了存储库链接