Visual Basic 中的逻辑回归分类

• 下载源代码 - 88.9 KB
• 下载最新源代码 - https://github.com/chlohe/VBML

引言

逻辑回归是一种令人兴奋的统计学方法，它允许我们在因变量是分类变量时，发现数据中的关系。因此，它吸引了许多统计学家的目光，以至于我的学校用它来帮助他们预测 A-level 成绩。

在本文中，我们将讨论一种简单的二元（仅输出“是”或“否”）逻辑回归在 Visual Basic 中的实现，并用它来根据电子表格中的数据进行预测。

背景

超级重要术语

假设 (Hypothesis) – 我们如何预测某事物的运作方式（例如，“我假设身高、年龄和体重之间的关系由函数 w = 5h + 2a + 1 给出”）。

参数向量 (Parameter Vector) – 包含你假设的系数的向量（例如，在之前的体重-身高模型中，5、2 和 1 包含在参数向量中）。它们有时会用希腊字母 θ 表示。

特征 (Feature) – 对被观测现象的可测量属性（例如，在之前的体重-身高模型中，身高和年龄是特征）。

似然度 (Likelihood) – 在给定参数向量的情况下，使用某个假设得到某个数据集的概率。

后验概率 (Posterior Probability) – 在给定数据集的情况下，获得具有某个参数向量的某个假设的概率。

如何将参数向量和值转化为假设？

很简单。

以体重预测器为例，设 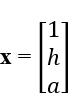和 。

我们想得到 w = 5h + 2a + 1。嗯。

如果我们乘以 x 中的每个元素与其在 **θ** 中的对应元素，我们会得到

h(x) = 1*1 + 5*h + 2*a

更抽象地说，对于 和 ，我们的假设是 。

这可以通过 `for` 循环完成，或者，如果你想做得更巧妙，可以使用矩阵乘法 (**x**^T**θ**)。

如何将假设转化为预测？

现在我们有了假设，我们需要做出预测——我们需要找到一种函数，将 h(x) 映射到 1 和 0 之间的某个值（分别代表“是”和“否”）。碰巧，一位名叫 Pierre François Verhulst 的数学家在研究人口增长时，恰好找到了这样一个函数：标准的逻辑函数（也称为“sigmoid”函数，因为它看起来像一个“s”）。

我们只需将我们的假设代入即可获得预测。如果函数不确定，它会返回一个分数：0.9 表示它很有可能是一个 1；0.4 是一个不太确定的 0。

等一下，θ 的值是怎么来的？

假设我们有训练示例数据，现在我们面临一个优化问题：找到 θ 的值，以最小化我们预测中的错误（从而优化我们的模型）。这个问题可以分解为两部分：

第一部分：我们错了多少？

对于每个向量 θ，我们需要计算基于这些值的模型错误程度。我们将使用的误差度量是负对数似然。

我们这样定义它：

这些情况的图表如下所示：

其中红线显示 。我们可以看到，函数在 x = 0 和 x = 1 处有渐近线，并且它们会严厉惩罚错误预测（当 y = 0 但我们预测了类似 0.9 时）。我们可以将这些表达式合并：

其中 N 是 **x** 中的示例数，y_i 是 **y** 中的第 i 个值，x_i 是 **x** 中的第 i 个示例。

请注意，当 y_i = 0 时，求和的第一项变为 0；当 y_i = 1 时，第二项变为 0。我们取对数变换是为了使函数更容易处理——可能会出现下溢的小数会变得不那么小；乘法变成加法。你可以在这里找到一个非常好的推导：http://www.robots.ox.ac.uk/~az/lectures/ml/2011/lect4.pdf。

第二部分：如何停止犯错？

要停止犯错，我们必须最小化我们的错误。最直观的方法之一就是利用初等微积分。逻辑回归的负对数似然函数可以被证明是凹函数——也就是说，存在一个唯一的全局最优值。

因此，我们对所有 **θ** 取偏导数，将它们乘以学习率（步长） α，然后从它们各自的原始值中减去：，其中 f 代表某个特征。多次迭代这个过程，基本上就是让我们更接近最优值——就像滑板手从山谷上滚下来一样——其中所有 **θ** 都有 。

在我们的逻辑函数的情况下，可以通过链式法则轻松获得导数。

因此，我们得到以下更新函数：

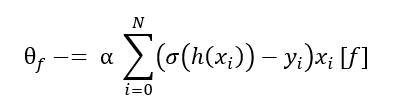
其中 f 是一个特征，α 是学习率，x_i [f] 是示例 x_i 中特征 f 的值。

总而言之，我们的算法如下所示：

对所有特征重复执行

如果梯度在合理阈值内，则退出循环。

优化优化器

我们可以看到，当接近最优值时，收敛速度会减慢。这是因为偏导数趋近于 0，步长变得非常小。我们可以通过对算法进行以下调整来抵消这一点：

• 将每个特征的平方偏导数记录在一个数组 中。
• 将每个特征的学习率除以最近 10 个偏导数之和的平方根。

这会在我们接近收敛时动态地改变学习率。

通过归一化所有特征，我们可以进一步加快收敛速度。我们也可以采用随机方法，在遍历每个训练示例后更新参数向量，尽管这种方法收敛得“不太好”。

需要更快的速度？

使用不同的算法，但请记住：矩阵求逆是费力的。牛顿法在有像样的线性代数库的情况下相当容易实现。

Using the Code

CSV 数据使用 `Load()` 方法加载。数据应在顶行包含标题。

Load("path/to/my_file_name.csv")

我们的逻辑函数和误差成本函数实现如下：

Function LogisticFunction(x)
    'Compute the value of the logistic function given input x
    'a sigmoid function has an S shape and is given by 1/(e^(-t))
    'e = 2.71... (Euler's number)

    Return (1 / (1 + Math.Exp(-x)))

End Function

Function LogisticCost()

    Dim cost As Double

    'Loop through all the training examples
    For i = 0 To exampleCount - 1

        Dim exampleCost As Double

        If exampleOutputs(i) = 0 Then
            exampleCost = Math.Log(1 - LogisticFunction(Hypothesis(exampleInputs(i))))
        Else
            exampleCost = Math.Log(LogisticFunction(Hypothesis(exampleInputs(i))))
        End If

        cost += exampleCost

    Next

    'Take average
    cost *= -1 / exampleCount

    Return Math.Abs(cost)

End Function

我们的优化算法在这里实现：

Sub Minimise()

    'Simple implementation of adagrad bc no way in hell 
    'am I implementing bfgs or anything that requires the hessan
    'gradient = X'(h(x) - y)

    Dim learningRate As New List(Of Double)
    Dim derivative As New List(Of Double)
    Dim pastGradientSquares As New List(Of List(Of Double))
    Dim sumOfPastGradientSquares As New List(Of Double)

    'Initialise all the variables
    For i = 0 To featureCount
        derivative.Add(1)
        learningRate.Add(0.01)
        sumOfPastGradientSquares.Add(0)
        pastGradientSquares.Add(New List(Of Double))
    Next

    lastCost = LogisticCost()
    deltaCost = 100

    'Do this until we converge (the derivative = 0ish)
    While (Math.Abs(deltaCost) > desiredDelta)

        Dim difference As New List(Of Double)
        Dim h As New List(Of Double)

        'Reset the derivative
        For i = 0 To thetas.Count
            derivative(i) = 0
        Next

        'Loop through the hypotheses and populate the list h

        For i = 0 To exampleCount - 1
            h.Add(LogisticFunction(Hypothesis(exampleInputs(i))))
        Next

        'Get the difference

        For i = 0 To exampleCount - 1
            difference.Add(h(i) - exampleOutputs(i))
        Next

        'Multiply by the features 

        For i = 0 To exampleCount - 1
            For j = 0 To featureCount - 1
                derivative(j) += difference(i) * exampleInputs(i)(j)

                'Update the list of previous squared derivatives
                pastGradientSquares(j).Add(Math.Pow(derivative(j), 2))

                'If we exceed 10 things, just remove the oldest entry 
                If pastGradientSquares(j).Count > 10 Then
                    pastGradientSquares(j).RemoveAt(0)
                End If

                'Update the sums
                sumOfPastGradientSquares(j) = Sum(pastGradientSquares(j))

            Next
        Next

        'Multiply by Learning Rate for this specific feature and get new thetas

        For i = 0 To featureCount - 1
            thetas(i) -= (learningRate(i) / _
            (Math.Sqrt(sumOfPastGradientSquares(i) + 0.00000001))) * derivative(i)
        Next

        Dim currentCost = LogisticCost()
        deltaCost = currentCost - lastCost

        'We need to look like we're doing something 
        'so here's something to keep users occupied
        Console.WriteLine("Training...  " + LogisticCost().ToString + _
                          " " + derivative(0).ToString) ' + " " + _
                          derivative(1).ToString + " " + derivative(2).ToString)

        lastCost = currentCost

    End While

End Sub

我们可以这样快速获得预测：

Function Predict(x)

    Return LogisticFunction(Hypothesis(x))

End Function

并且可以这样查看我们的分类器表现如何：

Sub Check()

    Dim correctlyClassified As Double = 0

    'Loop through results and see how many were classified correctly
    For i = 0 To exampleInputs.Count - 1

        Dim result As String
        If Predict(exampleInputs(i)) > 0.5 Then
            result = "Positive"
            If exampleOutputs(i) = 1 Then
                correctlyClassified += 1
            End If
        Else
            result = "Negative"
            If exampleOutputs(i) = 0 Then
                correctlyClassified += 1
            End If
        End If

        Dim trueClassification As String
        If exampleOutputs(i) = 1 Then
            trueClassification = "Positive"
        Else
            trueClassification = "Negative"
        End If

        Console.WriteLine(result + " and was actually " + trueClassification)

    Next

    Console.WriteLine("Correctly Classified " + _
       correctlyClassified.ToString + " out of " + exampleInputs.Count.ToString)

End Sub

演示

该分类器是在虚构数据上训练的，以模拟一些现实生活中的情况。使用以下数据，构建了一个模型来预测汽车碰撞，预测因素包括驱动轮、汽车年龄和天气状况。

由此产生的预测看起来有点像这样：

另一个数据集被用来预测学生是否会通过考试，预测因素是他们学习的小时数、他们之前的表现以及他们是否处于恋爱关系。

由此产生的预测是：

其他值得研究的方面

正则化

有时我们的模型可能会过拟合数据。这是一件坏事，因为虽然它在分类训练集方面可能表现更好，但在对新数据进行预测时可能不太适用。正则化可以帮助我们阻止这种情况。

多类分类

将事物分为“阳性”和“阴性”之外的类别。这可以粗略地通过为每个类别创建一个分类器来完成，将你的输入通过所有分类器，然后选择得分最高的分类。

例如，对于三个类别：猫、狗和桌子，一张猫的图片在猫分类器上可能得分为 0.9，在狗分类器上得分为 0.4，在桌子分类器上得分为 0.001。然后我们选择得分最高的分类器（0.9 分）并返回“这是一只猫”。

来源

• https://github.com/chlohe/VBML

历史

• 2016 年 12 月 19 日：初始版本