C#.NET:实现SVD++人工智能数据挖掘算法以产生基于评分预测的推荐
5.00/5 (14投票s)
在本文中,我们将讨论如何实现SVD++人工智能数据挖掘算法,以基于评分预测来产生推荐。
引言
在本文中,我们将讨论SVD++算法,它是现代推荐系统中功能强大且最成功的AI数据挖掘算法之一,该算法基于模型驱动的协同过滤(CF)方法来产生推荐。
通常,协同过滤是一种方法,它通过对活跃用户以及具有相似品味和偏好的其他用户的评分行为进行分析,以及对所评分项的受欢迎程度和兴趣(表示为过去对该项的评分次数)来进行分析,从而为活跃用户生成推荐[4]。
整个协同过滤过程可以归结为基于用户的协同过滤或基于项的协同过滤这两种主要方法[4]。
基于项的方法侧重于估计用户对某个项的偏好,而这种偏好仅基于该用户对相似项给予的评分。反过来,基于用户的方法用于根据其他用户先前对同一项的评分来估计用户对该项的偏好。换句话说,这两种方法实际上是通过将用户表示为已评分项的集合,将用户映射到项空间[1,3]。
为了产生推荐,协同过滤引擎通常处理两种不同对象类型的数据——用户或项。通常,由于这些对象在逻辑上不相关,因此很难进行比较。主要有两种方法可以促进这种比较:基于内存的协同过滤或基于模型的协同过滤[1,3,4]。
基于内存的方法通常使用k最近邻或k均值聚类等邻域算法,通过用户或项之间的基于距离的相似性来产生推荐。这些算法通常会搜索与活跃用户偏好相似的用户,并将这些用户过去已经推荐给活跃用户的项集推荐给活跃用户。类似地,以下算法旨在查找相似的项,并将它们与当前项一起推荐给特定用户[1,4]。
协同过滤的另一个特例是基于模型的方法。这种方法主要依赖于使用潜在因子模型和SVD算法系列(特别是SVD++算法),它们通过将项和用户都转换为相同的潜在因子空间,从而使它们能够完美比较,从而构成了一种替代方法[1,3,4]。
与其他算法一样,SVD++算法通过隐式反馈,基于评分预测来产生推荐。这通常通过分析用户或项的潜在因子来完成,这些潜在因子是从用户或项的效应数量中隐式推断出来的,例如给予“正面”或“负面”效应的倾向,或者所评分项的兴趣和受欢迎程度[1,3]。
SVD++算法的主要目标是通过找到评分矩阵数据中显示的潜在因子来解释现有评分。这通常是通过搜索来完成的,以基于评分预测数据模型中的数据找到用户或项的评分模式,该模型在算法的学习阶段构建和更新。这些模式用于对真实数据进行预测[1,3]。
与基于内存的算法相比,使用SVD++算法有许多好处,例如与基于内存的算法相比,它能更好地处理稀疏矩阵。这反过来又对处理大型数据集时的算法可扩展性产生了很大影响。此外,与k最近邻、k均值聚类等算法相比,它在预测性能上有所改善[1,3]。
最后,SVD算法家族在协同过滤领域变得非常流行。著名的Netflix Prize的获胜作品包含多个SVD模型,包括SVD++与受限玻尔兹曼机(RBM)的混合。通过使用SVD++算法,他们实现了比Netflix现有算法高10%的准确率[3]。
在本文中,我们将基于预测社交媒体网站上发布的文章数量并向读者社区推广的示例,讨论SVD++算法。
背景
用户到项评分预测数据模型
正如我们已经讨论过的,推荐引擎通常使用协同过滤(CF)方法来收集关于特定读者(即用户)对通常大量的文章(即项)的响应的统计数据。这些统计数据通常包括用户对项的评分以及描述所评分项的评论。这些数据,包括特定用户与其评分的项之间的依赖关系,被显式地存储在推荐数据库中[1]。
为了使用正在讨论的SVD++数据挖掘算法来预测未评分项的新评分,首先我们需要从推荐数据库中检索这些数据集并构建一个评分矩阵,其中每个用户对应一个被评分的特定项。下面的图1a说明了此评分矩阵。

实际上,从推荐数据库检索到的这些数据集通常是不完整的,因为并非所有用户都会对他们查看过的每篇文章提供特定的评论或评分。因此,我们获得的评分矩阵是一个稀疏矩阵,其中包含许多项的未知评分。如图1a所示,未知评分用“?”表示[1,3]。
此外,正如我们可能注意到的,正在讨论的评分矩阵实际上缺乏充分描述用户给某个特定项的每个评分的数据。此外,该矩阵也没有显示任何关于用户和项相似性,以及每个特定项的“正面”或“负面”方面的数据,而这些方面通常对正确的评分预测有很大的影响。这些数据缺失的主要原因是,上述大多数效应可以被设想或观察到,但永远无法用代数来衡量[1,3]。
这就是为什么SVD++数据挖掘算法在预测评分时,基本上只依赖于评分矩阵提供的现有数据。通过观察图1a所示的评分矩阵,我们可以注意到至少有三种效应体现在该矩阵提供的数据中[1]。
-
第一种效应,它影响评分预测,显然是“平均评分”。它使我们能够确定自收集特定用户和项的统计数据以来,整个项域的评分情况;
-
第二种效应是单个用户给许多项的评分集合,这代表了用户给予“正面”或“负面”评分的倾向;
-
第三种效应是过去给某个项的评分集合。这种效应反过来又与项的受欢迎程度和兴趣密切相关;
与用户和项相似性等其他效应不同,这三种效应可以表示为代表它们的参数的数量。以下图1b显示了这些效应。

这些参数是我们将在SVD++数据挖掘算法中使用,并将在下面的下一节中详细讨论的评分预测数据模型的主要构建块[1,3]。
在本文的下一节中,我们将讨论如何使用诸如平均评分、基线预测器和代表用户或项在评分矩阵检索数据中表现出的不同效应的因子向量等参数来估计未评分项的新评分[1,3,5]。
基线预测器
为了预测评分,各种效应的数据通常表示为一组参数,其值描述了用户评分行为或受用户或项的特定领域影响的许多因素影响的项的受欢迎程度。这些参数通常称为“基线预测器”。根据SVD++数据挖掘算法,为了预测评分,我们将主要处理两种类型的基线预测器:\(b_i^U\)和\(b_j^I\),它们分别代表用户\(i\)和项\(j\)的评分特定效应。在大多数情况下,这些基线预测器通常用作基线估计公式的参数[1,3,4,5]。
根据定义,“基线估计”是一个幅度,它通常包括表示为\(\mu\)的整体平均评分以及用户\(i\)或项\(j\)的基线预测器\(b_i^U\)和\(b_j^I\)。基线估计的最基本表示是这些参数的总和,可以表述如下:
, 其中\(\mu\)——所有项的总体平均评分,\(b_{i}^{U}\)——用户\(i\)的基线预测器,\(b_{j}^{I}\)——项\(j\)的基线预测器。基线估计是我们用来根据用户或项的不同效应来考虑所预测项的评分的基本公式。每个用户或项的基线预测器值集表示为两个向量\(b^{U}\)和\(b^{I}\)。
基线预测器之和通常被解释为与总体平均评分\(\mu\)的标准差\(b_{i}^{U} +b_{j}^{I}\)。标准差是一个幅度,其值很大程度上取决于受各种因素(如用户批评或项的受欢迎程度等)影响的用户或项效应的数量。例如,假设我们需要预测文章\(j\)的评分,其受欢迎程度比平均值\(\mu =3.24\)高\(b_{j}^{I} =+0.78\),由用户\(i\)评分,该用户倾向于给其他文章的评分比平均值低\(b_{i}^{U} =-0.32\)。让我们使用基线估计公式(1)计算预测评分值:\(b_{i,j} =3.24-0.32+0.78=3.7\)。显然,预测评分\(b_{i,j} =3.7\)高于平均评分[1,3,4,5]。
正如最初看来,除了基线估计,计算用户给项的预测评分可能还有其他方法。特别是,您可能也认为我们可以计算所有项的平均评分,然后从每个项的评分中减去该值。但事实并非如此[1,3,4,5]。
相反,为了有效地预测新评分,我们必须通过获得\(\mu\)、\(b_{i}^{U}\)、\(b_{j}^{I}\)的值来最小化预测误差,以便基线估计\(b_{i,j}\)能最好地近似现有评分。
此外,还有许多方法可以近似这些值,包括普通最小二乘法(OLS)、随机梯度下降(SGD)等,我们将在下一篇文章的后续章节中更详细地讨论。
正如我们已经知道的,基线估计公式**(1)**是总和,它包含平均评分\(\mu\)或基线预测器\(b_{i}^{U}\)和\(b_{j}^{I}\)等幅度,每个幅度都代表用户\(i\)或项\(j\)的特定效应。根据基线估计评分预测的基本思想,代表不同用户和项效应的总参数数量可以是可选的\(b_{i,j} =\mu +b_{i}^{U} +b_{j}^{I} +....\)。这意味着,我们也可以向基线估计公式(1)添加更多参数来表示特定效应,如特定用户和项的相似性,以提供更好的预测评分近似。要做到这一点,我们只需将这些参数的值添加到平均评分和基线预测器现有值之和中[1,3,4,5]。
通常,用户\(i\)的基线预测器\(b_{i}^{U}\)和项\(j\)的基线预测器\(b_{j}^{I}\)描述略有不同的效应。换句话说,用户和项的基线预测器值都描述了逻辑上不相关的效应。例如,用户基线预测器用于估计用户给予更高或更低评分的倾向,而项基线预测器的值通常表示过去典型地给予特定项的评分的效应。根据这一事实,使用基线估计的SVD++数据挖掘算法可能无法简单地“收敛”,从而阻止我们获得所需的评分近似。“收敛”是指算法给出先前讨论的数据模型的最佳近似的阶段[1,3,4,5]。
类似地,如果大多数用户没有给出任何评分,并且我们之前讨论的评分矩阵是一个稀疏矩阵,那么我们会遇到相同的情况。例如,如果一个特定用户只对5个项目中的1个进行了评分,那么就很难估计该用户将如何对剩余的项目进行评分,并将其表示为用户基线预测器的单个值。反过来,过去给予某个项目的评分的效应并不能描述对该项目进行评分的用户的评分行为,反之亦然[1,3,4,5]。
总的来说,一个新评分可以由用户对最常评分项的现有评分数量来表示的假设很难被证明。反过来,一个新评分仅根据不同用户过去对该项目的评分来估计也是很难证明的。此外,作为用户和项域的“偏差”的基线预测器\(b_{i}^{U}\)和\(b_{j}^{I}\)的值,由于这些效应中的大多数可以通过实验来确定而不是用代数来表达,因此很难调整。这些效应中的大多数并不明显,这意味着我们可以揭示和区分这些效应,但无法估计它们对评分预测的影响。例如,很难将某些用户和项的相似性表示为我们通常用于估计所预测评分的某个参数的值[1,3,4,5]。
SVD++数据挖掘算法在预测新评分时,实际上会遇到诸如无法估计新评分(已为许多类似项提供过评分)等问题[1,3,4,5]。
在下一节中,我们将讨论如何通过使用用户和项的因子向量以及基线估计公式来改进基线估计。
用户和项的因子向量
正如我们已经讨论过的,所预测的评分基本上取决于各种用户或项效应的多样性,例如每个用户的个人评分行为以及每个被评分项的特定受欢迎程度。通常,基于这些效应来预测评分非常困难,因为它们被表示为基线预测器\(b_{i}^{U}\)和\(b_{j}^{I}\)等参数的单个标量值,这些参数包含在基线估计中。这些参数的单个标量值无法充分解释通常大量的用户或项的各种不同效应。因此,这些作为“偏差”的参数值无法正确调整,以在预测评分时提供所需的近似值[1,3,4,5]。
因此,为了实现SVD++挖掘算法的收敛以及对正在预测的新评分的所需近似,我们需要将两个因子向量\(\overline{u_{i} }=\{ u_{0} ,u_{1} ,u_{2} ,...,u_{k-1} ,u_{k} \} |\overline{u_{i} }\in R^{k} \)和\(\overline{v_{j} }=\{ v_{0} ,v_{1} ,v_{2} ,...,v_{k-1} ,v_{k} \} |\overline{v_{j} }\in R^{k} \)添加为上述基线估计公式(1)的参数。图2说明了评分矩阵,其中每个用户或项都与特定的因子向量\(\overline{u_{i} }\)或\(\overline{v_{j} }\)相关联:

因此,用户特有的效应(包括用户的评分行为)以及项的效应(如项的受欢迎程度)都以两个k维的潜在因子向量的形式表示。向量\(\overline{u_{i} })\)通常包含主要描述用户\(i\)对不同效应(如倾向于给受欢迎的项更高的或更低的评分)的亲和力的潜在因子。同时,向量\(\overline{v_{j} }\)包含那些可以解释为项\(j\)的受欢迎程度(属于具有相似特征的项组等)的潜在因子。通过使用因子向量,我们将每个用户或项映射到潜在因子空间。每个用户或项的这些向量的组合通常表示为两个因子矩阵\(\overline{\overline{U}} \)和\(\overline{\overline{V}} \)[1,3,4,5]。
通过将因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)添加到基线估计公式中,我们实际上对这些参数进行了分解,这些参数的标量值代表了用户或项的特定效应。这些因子向量的组成部分实际上是偏差的集合,通过调整这些值的变化,我们实际上定义了特定用户或项对某个效应的亲和力。通过这样做,我们实际上通过对特定用户和项的这两个潜在因子向量进行基于距离的近似来识别具有相关效应的用户和项。由于由一组逻辑上无法解释的潜在因子表示的大多数用户和项效应,因此对新用户和项的评分预测变成了一个非线性问题[1,3,4,5]。
使用因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)来提供更好的评分预测近似的技术源于传统的SVD算法,在该算法中,这些因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)是特征向量,它们构成一个正交基。每个用户和项向量之间的近似距离基本上代表了由这些潜在因子解释的用户和项之间的相似性。这通常通过执行低秩评分矩阵近似来完成,从而降低了用户和项因子潜在空间的维度。这种潜在因子空间的维度通常通过将评分矩阵分解为由“左”或“右”奇异正交向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)组成的两个矩阵,以及包含特征值\(\delta _{i,j} \)的对角矩阵来实现,该对角矩阵位于该矩阵的对角线上。实际上,在降低维度的过程中,我们只对那些与具有最大值的特征值完全对应的正交向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)感兴趣。每个特征值可以表示为这些向量的内积:\(\delta _{i,j} =\sum _{i,j\in D}u_{i} v_{j}^{T} ) [6,7,8,9]\)。
然而,在处理具有超过55%稀疏度的评分矩阵时,使用传统SVD算法会导致未定义的预测结果,因为近一半的评分是未知的。不幸的是,当评分矩阵不完整(例如,不包含所有评分)时,无法找到奇异值分解[1,3,4,5]。
为了预测评分,我们通常会近似这些因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\),然后计算这些向量的内积\(\overline{u_{i} v_{j}^{T} }\),然后将其加到平均评分值和基线预测器值之和中,根据上述基线估计公式[1,3,4,5]。
因此,让我们完成基线估计公式,将其转换为我们将用于正在讨论的SVD++数据挖掘算法来计算预测评分值的通用公式:
, 其中\(\mu\)——所有项的总体平均评分,\(b_{i}^{U}\)——用户的基线预测器,\(b_{j}^{I}\)——项的基线预测器,\(\overline{u_{i} v_{j}^{T} }\)——两个因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)的内积。
与基线预测器一样,用户或项因子向量的内积是一个标量值,表示平均评分幅度的偏差。有许多方法允许我们使用此公式找到预测评分,我们将在本文的接下来的两个章节中进行详细讨论。
普通最小二乘法(OLS)
在本节中,我们将讨论如何利用SVD++数据挖掘算法,基于从现有评分矩阵中检索到的数据来预测评分。显然,新评分值是通过使用公式(2)计算的。为此,我们实际需要的是诸如整个项域的平均评分\(\mu\),基线预测器\(b_{i}^{U}\)和\(b_{j}^{I}\),以及因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)等参数的值。阻碍我们正确评分预测的主要问题是,这些参数的值对于所有未评分项都是未定义的,并且评分矩阵不包含关于被评分用户或项的任何明确提供的数据[1,3,4,5]。
根据正在讨论的SVD++数据挖掘算法的基本思想,为了获得这些参数的值并计算新评分,我们只需根据平均评分\(\mu\),基线预测器\(b_{i}^{U}\)和\(b_{j}^{I}\)以及因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)的值来“训练”我们的评分预测数据模型。在学习阶段,我们通常会更新现有评分的平均评分、基线预测器和因子向量的值,以最小化预测误差精度,直到我们找到这些参数的值能够为正在预测的新评分提供最佳近似[1,3,4,5]。
误差精度最小化通常使用普通最小二乘法(OLS)进行。该方法实际上用于通过最小化观测响应(例如从评分矩阵中检索到的项的现有评分)与使用公式(2)计算的评分之间的差异的平方和来找到线性回归中参数的未知值,其中我们即将近似的解释参数值的总和。现有评分和估计评分之间的差异幅度通常是标准误差偏差,表示为\(\varepsilon\)。
具体来说,为了找到标准误差偏差值\(\varepsilon\),我们必须使用公式(2)计算每个用户和项组合的新评分值\(\stackrel{\frown}{r}_{i,j}\),然后从当前用户和项在评分矩阵中检索到的现有评分值\(r_{i,j}\)中减去该值。
然后,我们将使用此值来更新这些参数的值,以确保为每个正在预测的评分提供最佳近似。为此,我们实际上需要最小化整个评分域的误差平方和\(\varepsilon ^{2}\):
根据公式,我们需要找到这样一个目标线性函数,其误差偏差之和趋近于最小值。换句话说,我们必须获得(\(\mu , b_{i}^{U} , b_{j}^{I} ,u_{i} ,v_{j} \))解释性参数的那些值,使得误差平方和最小。最好的方法是使用下一篇文章的下一节中讨论的随机梯度下降(SGD)[1,3,4,5]。
正则化和过拟合
让我们花点时间看看如果我们使用这个公式(3)通过进行简单的线性回归来训练我们的评分预测数据模型,会发生什么。正如我们已经讨论过的,我们通常目标是找到解释性参数(\(\mu,b_{i}^{U},b_{j}^{I},u_{i},v_{j}\))的值,这些值允许我们找到一个线性函数来最小化下面的平方和。根据稍后将讨论的SVD++数据挖掘算法,我们将通过在一定数量的“周期”内迭代进行梯度下降来简单地调整(或“拟合”)这些参数的值,直到我们最终获得所需的误差偏差值,因为下面的平方和是最小的[1,3,4,5]。
正如我们可能注意到的,在每个“周期”中,这些参数的绝对值会逐渐增加,直到误差平方和等于零。在这种情况下,我们处理的是一个包含大量参数的线性回归,通常很容易训练。这样的线性回归通常在最少迭代次数时提供最佳近似。在特定次数的迭代(即“周期”)内拟合解释性参数值的过程会导致评分预测数据模型本身饱和,具有通常很大的值,同时失去“预测能力”(例如,在预测新评分时无法提供正确的结果)。这通常被称为“过拟合”[1,3,4,5]。
通常,为了正确预测评分,我们需要提供一种机制,通过向目标线性函数添加“噪声”效应来避免解释性参数的饱和,即参数的绝对值过大。这种“噪声”效应按比例应用于目标函数,因为这些解释性参数的值会增加。换句话说,“噪声”效应是与目标函数下降梯度的值成反比的上升梯度幅度:解释性参数的值越高,我们必须添加到目标函数值中的“噪声”效应就越多。这个过程通常称为“正则化”
随机梯度下降(SGD)
正如我们上面提到的,SVD++数据挖掘算法主要基于随机梯度下降(SGD)方法,该方法允许我们近似基线估计的参数值,以预测未评分项的新评分。这通常通过在多个周期内迭代更新这些参数的值来完成,直到算法收敛并给出这些参数的最佳近似,从而提供未评分项的正确评分预测。随机梯度下降的基本思想是我们实际上是通过向与实际梯度方向相反的方向移动来调整这些参数的值。这也被称为“反梯度”。整个随机梯度方法可以表示为以下公式:
, 其中\(w\)——需要调整的线性目标函数\(E(w)\)的参数;\(\eta\)——执行的梯度下降速度;
该公式的主要代数意义是,我们实际上获得了目标线性函数的梯度\(\nabla E(w^{(0)})\),并将其乘以实际的梯度下降速度,然后从参数\(w^{(0)}\)的当前值中减去这个值,以获得以下参数的新调整值\(w^{(1)}\)。
具体到SVD++数据挖掘算法,我们将需要从公式(3)中获得目标线性函数的梯度,然后将其添加到公式(5)的随机梯度下降公式中,我们将使用它来近似这些解释性参数的值。显然,为了计算目标线性函数的梯度,我们将不得不获得该函数每个参数的偏导数[1,3,4,5]。
此时,让我们回到普通最小二乘法(OLS)的讨论。正如我们已经讨论过的,我们必须找到一个线性目标函数,它通常允许我们最小化公式(3,4)中的误差平方和。
现在,让我们仔细看看我们的目标函数本身。您可能会注意到,下面的函数是多参数函数。显然,这些参数通常代表平均评分\(\mu\),基线预测器\(b_{i}^{U}\)和\(b_{j}^{I}\),因子向量\(u_{i}\)和\(v_{j}\),如前所述。为了获得这些参数的值,其中整个评分域的误差平方和最小,我们实际上必须找到以下函数的极值(即最小值),\(E(\mu ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})=0\)。现在,让我们花点时间看看我们如何找到这个极值。根据这种方法,我们将简单地计算该函数的梯度,该梯度通常表示为该函数每个参数的偏导数集合\(\nabla E=(\frac{\partial E}{\partial \mu } ;\frac{\partial E}{\partial b_{i}^{U} } ;\frac{\partial E}{\partial b_{j}^{I} } ;\frac{\partial E}{\partial u_{i} } ;\frac{\partial E}{\partial v_{j} } )\)。为此,我们将找到每个参数的偏导数。正如我们从公式(6)中已经注意到的,下面的目标函数由两个表达式的总和组成。第一个表达式是误差平方和,而第二个表达式是向平方和添加“噪声”效应的表达式。因此,为了简化整个公式(5)的梯度计算,我们通常将以下函数分解为\(L(\mu ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})\)或\(W(\lambda ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})\)的小函数,如下所示:
函数\(\nabla E(\mu ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})\)的梯度现在表示为以下函数梯度之和:\(\nabla L(\mu ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})\)和\(\nabla W(\lambda ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})\)
为了演示如何获得这些偏导数,我们至少找到第一个简单参数\(b_{i}^{U}\)的偏导数,它代表用户\(i\)的基线预测器:
正如我们可能从公式(6.4)中注意到的,\(L(\mu ,b_{i} ,b_{j} ,u_{i} ,v_{j})\)是一个复合函数,为了找到其偏导数,我们将使用链式法则,该法则允许我们将该函数的导数分解为两个导数的乘积,我们将分别找到它们:
通过使用链式法则,我们将把函数\(L(\mu ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})\)的偏导数表示为另一个参数\(\varepsilon _{i,j} =r_{i,j} -(\mu +b_{i}^{U} +b_{j}^{I} +u_{i}v_{j}^{T})\)的导数,该参数实际上代表了本文前面章节中详细讨论的误差幅度。作为执行特定代数变换的结果,我们将获得函数\(L(\mu ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})\)对参数)(b_{i}^{U}\)的偏导数:
类似地,我们将获得函数\(W(\lambda ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})\)对参数\(b_{i}^{U}\)的偏导数:
现在,让我们将公式(6.3)的这些部分相加,以获得目标线性函数的梯度\(\nabla E(\mu ,b_{i}^{U} ,b_{j}^{I} ,u_{i} ,v_{j})\),如下所示:
接下来,我们将使用类似的技术来获得目标线性函数\(\nabla E(\mu ,b_{i} ,b_{j} ,u_{i} ,v_{j})\)其余参数的偏导数,我们将在本节的后续段落中讨论。
既然我们已经通过获得该函数所有参数的偏导数来找到了目标线性函数的梯度,现在让我们将这些偏导数应用于每个目标函数参数的随机梯度公式(5):
现在,让我们看看我们实际获得了哪些公式。下面的每个公式(7.1-5)都用于在SVD++算法的学习阶段(将在下一篇文章中讨论)调整(或“更新”)评分预测数据模型的每个解释性参数。通过使用这些公式,我们将实际执行随机梯度下降,直到算法收敛,从而提供对正在训练的数据模型的正确近似。数据模型的最佳近似通常确保我们能够计算(即预测)未评分项的正确新评分[1,3,4,5]。
此时,让我们讨论这些公式的代数意义。这些公式中的每一个都源于本节开头讨论的随机梯度下降公式。根据随机梯度下降的主要思想,我们通常通过在某个目标线性函数的梯度相反的方向上来近似某个参数的值。这就是为什么梯度值从该参数的当前值中减去以执行以下参数值更新的原因。传统SGD公式与我们获得的公式集之间的主要区别在于,在这种特定情况下,我们目标线性函数的梯度的值被添加到每个参数的值中[1,3,4,5]。
我们通常使用前两个公式来更新基线预测器(\(b_{i}^{U}, b_{j}^{I} \))的值,这些预测器代表用户或项的效应,这些值是在处理评分矩阵时隐式获得的。我们进行更新,直到找到用户\(i\)和项\(j\)的基线预测器的那些值,它们能够正确近似平均评分\(\mu\)的标准差。图3a说明了基线预测器更新过程。

特别有趣的是最后两个公式(7.4)和(7.5),我们使用它们来更新由因子向量(\(\overline{u_{i} }, \overline{v_{j} }\))表示的潜在因子。与用于更新平均评分和基线预测器标量值的公式不同,下面的公式用于更新用户或项潜在因子的整个向量。这些公式实际上用于更新作为特定因子向量分量的每个潜在因子的值。在处理这些公式时,我们实际上是对这些向量的每个分量与误差\(\varepsilon _{i,j} \)和正则化系数\(\lambda\)的标量值进行标量乘法。结果是我们获得了更新的因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)。图3b说明了使用公式(7.4)和(7.5)来更新由用户或项因子向量表示的潜在因子值的集合。

通过更新因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\),我们实际上在近似这些向量之间的距离,该距离取决于误差\(\varepsilon _{i,j} \)的值。下面的距离实际上是特定用户和项的相似性,这取决于由这些解释性参数表示的特定效应,这些参数的值被分解为潜在因子集[1,3,4,5]。
SVD++数据挖掘算法要点
在本文前面的部分,我们已经详细讨论了SVD++数据挖掘算法的数学模型。现在是时候讨论SVD++算法的要点了。
SVD++算法根据其性质,是一种AI数据挖掘算法,通常包含两个主要阶段:“学习”阶段,在此期间我们实际上执行评分预测模型的“离线”训练;以及计算阶段,在此阶段我们将实际计算(即预测)评分矩阵中多个未评分项的新评分[1,3,4,5]。
初始化
SVD++算法的第一步是初始化阶段。在此阶段,我们将为评分预测数据模型分配初始值。让我们花点时间看看用户或项基线预测器向量\(\overline{b^{U} }\)和\(\overline{b^{I} }\)的分量将被赋给什么具体值。这些向量通常用零值初始化\(\overline{b^{U} }=\{ 0\} , \overline{b^{I} }=\{ 0\} \),因为我们最初没有关于用户或项效应的“隐式”数据。另一种情况是初始化因子矩阵\(\overline{\overline{U}} \)和\(\overline{\overline{V}} \),它们包含每个用户和项的潜在因子向量\(\overline{u_{i} }\)和\(\overline{v_{j} }\)的组合。正如我们已经讨论过的,在学习阶段之前,潜在因子的初始值通常是未定义的。为了避免“冷启动”问题,根据SVD++算法,我们所要做的就是将第一个用户\((i=0)\)和项\((j=0)\)的这些因子向量的第一个分量\(u_{0,0}\)和\(v_{0,0}\)分别初始化为任意值0.1和0.05:\(u_{i,j} \leftarrow 0.1\)\(v_{i,j} \leftarrow 0.05|i,j=0\)。
在初始化了基线预测器和因子向量之后,我们还必须计算整个项域的平均评分。我们通常只为评分值已存在的项计算平均评分:\(\mu \leftarrow AVG[r_{i,j} ]|\forall r_{i,j} \ne -1\)。或者,我们可以将平均评分变量\(\mu\)初始化为最低可能评分值。为了计算所有已存在评分的项的平均评分,我们必须遍历评分矩阵,对于每个评分,执行检查以确定该特定项的评分是否已存在。如果存在,我们将当前现有评分的值加到用于存储所有现有评分总和的变量值中。此外,我们还必须递增用于存储实际现有评分次数值的循环计数器变量。最后,我们必须将所有现有评分的总和除以其实际计数以获得平均评分值[1,3,4,5]。图4所示的框图说明了该算法。

由于SVD++算法的评分预测模型具有许多代表该模型特定特征的参数,例如学习速度\(\eta\)和正则化系数\(\lambda _{1}\)和\(\lambda _{2}\),我们还必须在SVD++算法的学习阶段之前为这些参数赋初值[1,3,4,5]。
学习阶段
此时,让我们仔细看看“学习”过程本身。与大多数现有人工智能数据挖掘和遗传算法类似,在计算未评分项的新评分之前,我们必须先在一定数量的周期内,在大量的训练样本(即现有评分)上训练我们的评分预测数据模型。根据SVD++算法的基本思想,我们将使用公式(7.1-5)通过执行随机梯度下降来更新平均评分\(\mu\)、基线预测器(\(b_{i}^{U}, b_{j}^{I} \))和因子向量(\(\overline{u_{i} }, \overline{v_{j} })\)的值,直到算法收敛,从而提供对正在预测的新评分的最佳近似[1,3,4,5]。
根据SVD++算法,在“学习”阶段,我们将遍历评分矩阵,对于由用户\(i\)给项\(j\)的每个现有评分\(r_{i,j} \),我们将执行以下步骤来实际更新基线估计的这些解释性参数(\(\mu , b_{i}^{U}, b_{j}^{I}, u_{i}, v_{j}\))的值,以最小化整个项域的误差平方\(\varepsilon _{i,j}^2\)的值:
- 使用公式(2)计算当前估计的评分值\(\stackrel{\frown}{r}_{i,j} \):\(\stackrel{\frown}{r}_{i,j} =\mu +b_{i}^{U} +b_{j}^{I} +\overline{u_{i} v_{j}^{T} }\);
- 通过从现有评分值中减去上一步得到的估计评分值\(\stackrel{\frown}{r}_{i,j}\)来找到误差值,如下所示:\(\varepsilon _{i,j} =r_{i,j} -\hat{r}_{i,j} \);
- 计算上一步得到的误差值的平方\(\varepsilon _{i,j}^{2} \),并将该值加到误差平方和中;
- 更新平均评分的当前值:\(\mu =\mu +\eta(\varepsilon _{i,j} -\lambda \mu)\)
- 更新用户\(i\)的基线预测器的当前值:\(b_{i}^{U} =b_{i}^{U} +\eta (\varepsilon _{i,j} -\lambda b_{i}^{U})\);
- 更新项\(j\)的基线预测器的当前值:\(b_{j}^{I} =b_{j}^{I} +\eta (\varepsilon _{i,j} -\lambda b_{j}^{I})\);
- 更新用户\(i\)的因子向量中每个潜在因子的值:\(u_{i} =u_{i} +\eta(\varepsilon _{i,j} v_{j}^{T} -\lambda u_{i})\);
- 更新项\(j\)的因子向量中每个潜在因子的值:\(v_{j}^{T} =v_{j}^{T} +\eta (\varepsilon _{i,j} u_{i} -\lambda v_{j}^{T})\);
通常,我们将迭代进行“学习”过程,直到算法收敛。算法的收敛性基本上是通过计算均方根误差(RMSE)来确定的,RMSE估计为步骤3中获得的误差平方和\(\varepsilon _{i,j}^2 \)的平方根,除以我们使用的训练样本数\(N_{i} \):\(RMSE=\frac{1}{N_{t} } \times \sqrt{\sum _{i,j\in D}\varepsilon _{i,j}^{2} } \)。通常,我们为评分矩阵中的每个特定现有评分计算误差平方值\(\varepsilon _{i,j}^{2} \),然后将其加到表示这些误差平方和的总值中。一旦我们获得了误差平方和的值,我们就在每个周期结束时计算RMSE。此时,我们实际测试学习过程是否已收敛。这通常通过计算当前均方根误差值RMSE与学习阶段前一个周期获得的均方根误差值之间的差值来完成。为了计算这个差值,我们实际上是从RMSE的先前值中减去当前值:(RMSE-RMSE_NEW)> eps,\(eps > 10e-4\)。之后,我们检查这些值之间的差是否大于\(eps\)变量的值,该变量表示误差的精度。如果是,我们将继续进行下一周期的训练,在该周期中,我们将再次对整个项域执行评分预测数据模型的更新。否则,由于差值小于\(eps\)的值,这意味着当前周期和前一个周期获得的平方和的值(即迭代)非常相似,我们只是终止数据模型训练过程。换句话说,我们通常继续学习过程,直到近似的RMSE值对于每个后续学习周期都相同并且不再变化[1,3,4,5]。
此外,在某些特殊情况下,SVD++算法的学习阶段会因上述数据模型过拟合等问题而退化。换句话说,我们可能会注意到,在学习阶段的每个周期中,RMSE的值实际上没有变化,数据模型也不再提供对正在预测的新评分的所需近似[1,3,4,5]。
在这种情况下,SVD++算法最有效的优化方法是减慢学习过程,方法是降低学习速度参数\(\eta\)的值。这通常通过验证当前RMSE值与先前RMSE值之间的差值是否超过特定阈值来完成。如果是,我们只需将参数\(\eta\)的值乘以一个系数,该系数实际上会减慢学习过程。这反过来有利于整个SVD++算法的快速收敛[1,3,4,5]。SVD++学习阶段的整个算法由图5说明。

预测评分
在训练了我们的评分预测数据模型之后,现在是时候计算每个未知评分的值了。要做到这一点,我们需要遍历评分矩阵,并检查每个评分,看当前用户\(i\)给项\(j\)的评分是否是未知评分。如果是,我们使用公式(2):\(\stackrel{\frown}{r}_{i,j} =\mu +b_{i}^{U} +b_{j}^{I} +\overline{u_{i} v_{j}^{T} }\)来简单地计算未知评分的值。在这种情况下,我们实际上是使用我们评分预测模型获得的当前用户\(i\)和项\(j\)的解释性参数值,并将其应用于以下公式来计算未评分项的评分值。通过执行这些计算,我们将获得用户\(i\)给项\(j\)的估计评分值[1,3,4,5]。
评分预测过程最有效的优化是,在每次新评分计算后,我们实际上需要“重新训练”评分预测数据模型。这反过来又可以提高预测质量,同时避免“冷启动”问题[1,3,4,5]。
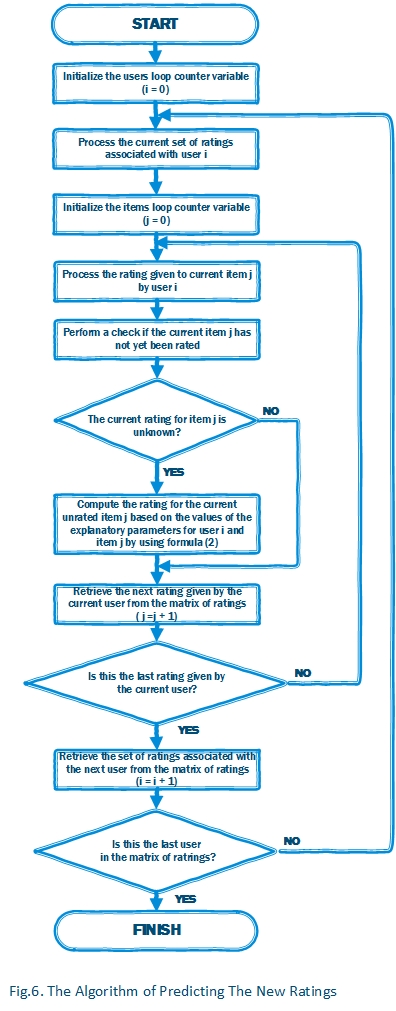
基于评分预测数据模型进行评分预测的算法由图6说明。
评估SVD++算法
在本节中,我们将讨论如何使用SVD++算法,通过预测用户社区对社交媒体网站上发布的排名前5的文章的评分来产生推荐。正如我们已经讨论过的,SVD++算法的输入数据集是文章评分矩阵,如下所示:

该矩阵的每一行代表一个特定用户给许多文章的评分集合。正如我们已经讨论过的,每个用户都有自己的品味和偏好,这些品味和偏好体现在图7所示的评分矩阵的数据中。反过来,每篇文章都有过去由许多用户给出的评分历史。
在此特定情况下,为了演示实现SVD++算法的代码进行的文章评分预测,我们构建了一个矩阵,其中包含“挑剔”用户4给出的评分,以及倾向于只给大多数文章“正面”评分(例如,是“慷慨”读者)的用户3给出的评分。此外,下面的评分矩阵包含其他用户的典型给分数据,这些用户给他们查看过的文章平均评分。这些“平均”用户是一个特别的关注点,因为为了评估所讨论算法的预测质量,我们主要目标是训练评分预测数据模型来预测“平均”用户可能给他们查看过的文章的评分。
我们特意选择了排名前5的文章,并按文章相似性将它们分为两类。在这种情况下,第一类包括关于C#编程的文章,而另一类由关于C++编程的文章组成。
现在,让我们花点时间看看“平均”用户0是如何根据代码执行结果获得的评分预测来评价文章“C#高级入门...”的。显然,用户0对这篇文章的预测评分为5.00分中的4.63分,因为用户0已经积极评价了许多类似的文章,并且该文章的先前平均评分通常为3.75。显然,这篇文章被推荐给用户0。
另一个特殊情况是用户2给文章“C#嵌套类教程”的评分。正如我们从上面的评分矩阵中看到的,用户2对同一篇文章的评分与用户0相似,但是这篇文章的先前平均评分为3.66,这显然低于前一个示例的平均评分。因此,对这篇文章预测的评分为5分中的3.90分,比前一个示例预测的评分低0.73分。这篇文章被推荐给用户2。
使用代码
下面一段代码执行评分预测数据模型的初始化。
static void Initialize()
{
// Constructing the matrix of user's latent factors by iteratively
// appending the rows being constructed to the list of rows MF_UserRow
for (int User = 0; User < MatrixUI.Count(); User++)
{
// Declare a list of items MF_UserRow rated by the current user
List<double> MF_UserRow = new List<double>();
// Add the set of elements equal to 0 to the list of items MF_UserRow.
// The number of elements being added is stored in Factors variable
MF_UserRow.AddRange(Enumerable.Repeat(0.00, Factors));
// Append the current row MF_UserRow to the matrix of factors MF_User
MF_User.Insert(User, MF_UserRow);
}
// Constructing the matrix of item's latent factors by iteratively
// appending the rows being constructed to the list of rows MF_ItemRow
for (int Item = 0; Item < MatrixUI.ElementAt(0).Count(); Item++)
{
// Declare a list of items MF_ItemRow rated by the current item
List<double> MF_ItemRow = new List<double>();
// Add the set of elements equal to 0 to the list of items MF_ItemRow
// The number of elements being added is stored in Factors variable
MF_ItemRow.AddRange(Enumerable.Repeat(0.00, Factors));
// Append the current row MF_ItemRow to the matrix of factors MF_Item
MF_Item.Insert(Item, MF_ItemRow);
}
// Intializing the first elements of the matrices of user's
// and item's factors with values 0.1 and 0.05
MF_User[0][0] = 0.1; MF_Item[0][0] = MF_User[0][0] / 2;
// Construct the vector of users baseline predictors by
// appending the set of elements equal to 0.The number of elements being
// appended is equal to the actual number of rows in the matrix of ratings
BS_User.AddRange(Enumerable.Repeat(0.00, MatrixUI.Count()));
// Construct the vector of items baseline predictors by appending
// the set of elements equal to 0. The number of elements appended
// is equal to the actual number of rows in the matrix of ratings
BS_Item.AddRange(Enumerable.Repeat(0.00, MatrixUI.ElementAt(0).Count()));
}
以下函数执行评分预测数据模型训练。
static void Learn()
{
// Initializing the iterations loop counter variable
int Iterations = 0;
// Initializing the RMSE and RMSE_New variables to store
// current and previous values of RMSE
double RMSE = 0.00, RMSE_New = 1.00;
// Computing the average rating for the entire domain of rated items
double AvgRating = GetAverageRating(MatrixUI);
// Iterating the process of the ratings prediction model update until
// the value of difference between the current and previous value of RMSE
// is greater than the value of error precision accuracy EPS (e.g. the learning
// process has converged).
while (Math.Abs(RMSE - RMSE_New) > EPS)
{
// Assign the previously obtained value of RMSE to the RMSE variable
// Assign the variable RMSE_New equal to 0
RMSE = RMSE_New; RMSE_New = 0;
// Iterate through the matrix of ratings and for each existing rating compute
// the error value and perform the stochastic gradient descent to update
// the main parameters of the ratings prediction model for the current user and item
for (int User = 0; User < MatrixUI.Count(); User++)
{
for (int Item = 0; Item < MatrixUI.ElementAt(0).Count(); Item++)
// Perform a check if the current rating in the matrix of ratings is unknown.
// If not, perform the following steps to adjust the values of baseline
// predictors and factorization vectors
if (MatrixUI[User].ElementAt(Item) > 0)
{
// Compute the value of estimated rating using formula (2)
double Rating = AvgRating + BS_User[User] +
BS_Item[Item] + GetProduct(MF_User[User], MF_Item[Item]);
// Compute the error value as the difference
// between the existing and estimated ratings
double Error = MatrixUI[User].ElementAt(Item) - Rating;
// Output the current rating given by the current user to the current item
Console.Write("{0:0.00}|{1:0.00} ", MatrixUI[User][Item], Rating);
// Add the value of error square to the current value of RMSE
RMSE_New = RMSE_New + Math.Pow(Error, 2);
// Update the value of average rating for the entire domain of ratings
// by performing stochastic gradient descent using formulas (7.1-5)
AvgRating = AvgRating + TS * (Error - L1 * AvgRating);
// Update the value of baseline predictor of the current user
// by performing stochastic gradient descent using formulas (7.1-5)
BS_User[User] = BS_User[User] + TS * (Error - L1 * BS_User[User]);
// Update the value of baseline predictor of the current item
// by performing stochastic gradient descent using formulas (7.1-5)
BS_Item[Item] = BS_Item[Item] + TS * (Error - L1 * BS_Item[Item]);
// Update each component of the factorization vector for
// the current user and item
for (int Factor = 0; Factor < Factors; Factor++)
{
// Adjust the value of the current component of the user's
// factorization vector by performing stochastic gradient
// descent using formulas (7.1-5)
MF_User[User][Factor] += TS * (Error * MF_Item[Item][Factor] +
L2 * MF_User[User][Factor]);
// Adjust the value of the current component of the item's
// factorization vector by performing stochastic gradient
// descent using formulas (7.1-5)
MF_Item[Item][Factor] += TS * (Error * MF_User[User][Factor] +
L2 * MF_Item[Item][Factor]);
}
}
// Output the value of unknown rating in the matrix of ratings
else Console.Write("{0:0.00}|0.00 ", MatrixUI[User][Item]);
Console.WriteLine("\n");
}
// Compute the current value of RMSE (root means square error)
RMSE_New = Math.Sqrt(RMSE_New / (MatrixUI.Count() * MatrixUI.ElementAt(0).Count()));
Console.WriteLine("Iteration: {0}\t RMSE={1}\n\n", Iterations, RMSE_New);
// Performing a check if the difference between the values
// of current and previous values of RMSE exceeds the given threshold
if (RMSE_New > RMSE - Threshold)
{
// If so, reduce the values of training speed and threshold
// by multiplying each value by the value of specific coefficients
TS *= 0.66; Threshold *= 0.5;
}
Iterations++; // Increment the iterations loop counter variable
}
}
以下代码片段执行预测评分计算。
public static void Predict()
{
// Computing the average rating for the entire domain of rated items
double AvgRating = GetAverageRating(MatrixUI);
Console.WriteLine("We've predicted the following ratings:\n");
// Iterating through the MatrixUI matrix of ratings
for (int User = 0; User < MatrixUI.Count(); User++)
for (int Item = 0; Item < MatrixUI.ElementAt(0).Count(); Item++)
// For each rating given to the current item by the current user
// we're performing a check if the current item is unknown
if (MatrixUI[User].ElementAt(Item) == 0)
{
// If so, compute the rating for the current
// unrated item used baseline estimate formula (2)
MatrixUI[User][Item] = AvgRating + BS_User[User] +
BS_Item[Item] + GetProduct(MF_User[User], MF_Item[Item]);
// Output the original rating estimated for the current item
// and the rounded value of the following rating
Console.WriteLine("User {0} has rated Item {1} as {2:0.00}|{3:0.00}", User,
Item, MatrixUI[User][Item], Math.Round(MatrixUI[User][Item]));
}
Console.WriteLine();
}
以下例程执行两个向量的内积计算。
public static double GetProduct(List<double> VF_User, List<double> VF_Item)
{
// Initialize the variable that is used to
// store the inner product of two factorization vectors
double Product = 0.00;
// Iterating through the two factorization vectors
for (int Index = 0; Index < Factors; Index++)
// Compute the value of product of the two components
// of those vectors having the same value of index and
// add this value to the value of the variable Product
Product += VF_User[Index] * VF_Item[Index];
return Product;
}
以下代码片段计算整个项域的平均评分。
public static double GetAverageRating(List<list<double>> Matrix)
{
// Initialize the variables Sum and Count to store the values of
// sum of existing ratings in matrix of ratings and the count of
// existing ratings respectively
double Sum = 0; int Count = 0;
// Iterating through the matrix of ratings
for (int User = 0; User < Matrix.Count(); User++)
for (int Item = 0; Item < Matrix[User].Count(); Item++)
// For each rating performing a check if the current rating is unknown
if (Matrix[User][Item] > 0)
{
// If not, add the value of the current rating to the
// value of variable Sum
Sum = Sum + Matrix[User][Item];
// Increment the loop counter variable of existing ratings by 1
Count = Count + 1;
}
// Compute and return the value of average
// rating for the entire domain of existing ratings
return Sum / Count;
}
此代码段用于从文件中加载评分矩阵。
public static void LoadItemsFromFile(string Filename, List<list<double>> Matrix)
{
// Intializing the file stream object and open the file
using (System.IO.FileStream fsFile = new System.IO.FileStream(Filename,
System.IO.FileMode.Open, System.IO.FileAccess.Read, System.IO.FileShare.Read))
{
// Initializing the stream reader object
using (System.IO.StreamReader fsStream = new System.IO.StreamReader(
fsFile, System.Text.Encoding.UTF8, true, 128))
{
string textBuf = "\0";
// Retrieving each line from the file until we reach the end-of-file
while ((textBuf = fsStream.ReadLine()) != null)
{
List<double> Row = new List<double>();
if (!String.IsNullOrEmpty(textBuf))
{
string sPattern = " ";
// Iterating through the array of tokens and
// append each token to the array Row
foreach (var rating in Regex.Split(textBuf, sPattern))
Row.Add(double.Parse(rating));
}
// Append the current row to the matrix of ratings
Matrix.Add(Row);
}
}
}
}
输出
本文讨论的代码会产生以下输出,该输出基于从RATINGS.TXT文件中加载的评分矩阵。首先,代码输出原始矩阵,其中未知评分表示为(???)。之后,代码执行评分预测数据模型的训练。在学习阶段,它输出现有评分和近似评分的矩阵,其中现有评分和近似评分值由“|”字符分隔。输出的每个块是为学习阶段的每次迭代(即“epoch”)生成的。在每个块的底部,列出的代码通常会打印迭代次数(即“epoch”)和当前迭代的RMSE(均方根误差)值,如图8所示。

Matrix of ratings given to items by users
??? 3,00 4,00 5,00 2,00
3,00 5,00 2,00 2,00 5,00
5,00 3,00 ??? 4,00 3,00
5,00 5,00 5,00 ??? 5,00
2,00 3,00 ??? 2,00 2,00
0,00|0.00 3,00|3,57 4,00|3,54 5,00|3,57 2,00|3,64
3,00|3,56 5,00|3,52 2,00|3,62 2,00|3,56 5,00|3,41
5,00|3,53 3,00|3,64 0,00|0.00 4,00|3,58 3,00|3,61
5,00|3,58 5,00|3,64 5,00|3,67 0,00|0.00 5,00|3,75
2,00|3,75 3,00|3,65 0,00|0.00 2,00|3,58 2,00|3,51
Iteration: 0 RMSE=1,16542197178961
0,00|0.00 3,00|3,57 4,00|3,54 5,00|3,51 2,00|3,57
3,00|3,55 5,00|3,53 2,00|3,58 2,00|3,51 5,00|3,42
5,00|3,57 3,00|3,65 0,00|0.00 4,00|3,55 3,00|3,58
5,00|3,72 5,00|3,76 5,00|3,76 0,00|0.00 5,00|3,78
2,00|3,55 3,00|3,50 0,00|0.00 2,00|3,41 2,00|3,37
Iteration: 1 RMSE=1,1079120145992
*************************************************
0,00|0.00 3,00|2,80 4,00|4,16 5,00|4,78 2,00|2,15
3,00|2,85 5,00|5,02 2,00|2,17 2,00|1,99 5,00|4,95
5,00|4,43 3,00|3,36 0,00|0.00 4,00|4,38 3,00|2,82
5,00|5,29 5,00|5,21 5,00|4,72 0,00|0.00 5,00|4,81
2,00|2,29 3,00|2,62 0,00|0.00 2,00|1,89 2,00|2,29
Iteration: 464 RMSE=0,235306704248189
0,00|0.00 3,00|2,80 4,00|4,16 5,00|4,78 2,00|2,15
3,00|2,85 5,00|5,02 2,00|2,16 2,00|1,99 5,00|4,95
5,00|4,43 3,00|3,36 0,00|0.00 4,00|4,38 3,00|2,82
5,00|5,29 5,00|5,21 5,00|4,72 0,00|0.00 5,00|4,81
2,00|2,29 3,00|2,62 0,00|0.00 2,00|1,89 2,00|2,29
Iteration: 465 RMSE=0,235296693918684
0,00|0.00 3,00|2,80 4,00|4,16 5,00|4,78 2,00|2,15
3,00|2,85 5,00|5,02 2,00|2,16 2,00|1,99 5,00|4,95
5,00|4,43 3,00|3,36 0,00|0.00 4,00|4,38 3,00|2,82
5,00|5,29 5,00|5,21 5,00|4,72 0,00|0.00 5,00|4,81
2,00|2,29 3,00|2,62 0,00|0.00 2,00|1,89 2,00|2,29
Iteration: 466 RMSE=0,235286707713274
We've predicted the following ratings:
User 0 has rated Item 0 as 4,63|5,00
User 2 has rated Item 2 as 3,90|4,00
User 3 has rated Item 3 as 4,98|5,00
User 4 has rated Item 2 as 1,69|2,00
The target matrix of ratings:
5,00 3,00 4,00 5,00 2,00
3,00 5,00 2,00 2,00 5,00
5,00 3,00 4,00 4,00 3,00
5,00 5,00 5,00 5,00 5,00
2,00 3,00 2,00 2,00 2,00
在上面的输出底部,以下代码会打印出在计算阶段为特定用户和项预测的评分。它还打印出评分矩阵,其中所有缺失的评分都已替换为预测的评分值。
参考文献
- Yehuda Koren. Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model. AT&T Labs – Research. © 2008;
- Rajeev Kumar, B. K. Verma, Shyam Sunder Rastogi. Social Popularity based SVD++ Recommender Systems. International Journal of Computer Applications (0975 – 8887). Volume 87 – No.14, February 2014;
- Stephen Gower. Netflix Prize and SVD. © April 18th 2014;
- Collaborative Filtering. From Wikipedia, the free encyclopedia https://en.wikipedia.org/wiki/Collaborative_filtering;
- Michael D. Ekstrand, John T. Riedl, Joseph A. Konstan. Collaborative Filtering Recommender Systems. Foundations and Trends® in Human–Computer Interaction Vol. 4, No. 2 (2010) 81–173. © 2011;
- Tianqi Chen, Zhao Zheng, Qiuxia Lu, Weinan Zhang, Yong Yu. Feature-Based Matrix Factorization. Apex Data & Knowledge Management Lab Shanghai Jiao Tong University. © 2011;
- Badrul Sarwar, George Karypis, Joseph Konstan, and John Riedl. Incremental Singular Value Decomposition Algorithms for Highly Scalable Recommender Systems. GroupLens Research Group / Army HPC Research Center Department of Computer Science and Engineering University of Minnesota. © 2014;
- Serdar Sali. Using SVD to Predict Movie Ratings. Department of Computer Science, Jack Baskin School of Engineering at UC Santa Cruz, California, USA. © 2008;
- Alan Kaylor Cline, Inderjit S. Dhillon. Computation of the Singular Value Decomposition. The University of Texas at Austin. © 2006;
关注点
SVD++ AI数据挖掘算法是著名的Netflix Prize的获胜作品。使用SVD++算法预测电影评分,与大多数基于内存的算法(如k最近邻和k均值聚类)相比,可以将预测质量提高10%。也许一些爱好者能够改进SVD++算法,将预测质量大幅提高10%以上,相比于本文讨论的算法。
历史
- 2017年2月1日 - 文章首次修订发布
