通用图灵机模拟器
5.00/5 (20投票s)
本文描述了通用图灵机模拟器的实现和测试。
引言
本文描述了通用图灵机模拟器的实现和测试。该代码是将我之前在华盛顿州立大学(电子工程与计算机科学系)教授自动机理论(2000年1月至2002年12月)时实现的旧 Borland C++ 版本转换到 Visual Studio 2010 下的非托管 C++。
注意: 本文摘自我未出版的教科书《应用算法与数据结构》第13章“自动机理论应用,第三部分”的节选。

希尔伯特,大卫
(1862年1月23日 - 1943年2月14日) 德国数学家,于1900年在巴黎国际数学家大会上公布了23个研究问题。在他的演讲《数学问题》中,他概述了他那个时代的几乎所有数学,并试图提出他认为对20世纪数学家重要的难题。许多问题至今已被解决,每一个解决方案都是一个重要的事件。(《新英格兰百科全书》,1991年,第5卷,第922-923页。)

图灵,艾伦·马蒂森
(1912年6月23日 - 1954年6月7日) 英国数学家,解决了希尔伯特的判定问题。二战期间,他在破解德国恩尼格玛密码方面发挥了关键作用。(照片来源:Barendregt, H.P. Lambda微积分,其语法与语义。 阿姆斯特丹:North-Holland,1981年。)
图灵机
图灵定义了一类计算机器,并在他的一篇有影响力的论文中使用了它们,在该论文中他证明了希尔伯特的判定问题(Decision Problem 或 Halting Problem)是不可判定的。(Turing, A.M. “论可计算数及其在判定问题上的应用。” 伦敦数学学会会报, 第42卷,1937年,第230-265页;以及“论可计算数及其在判定问题上的应用。更正” 伦敦数学学会会报, 第43卷,1937年,第544-546页。)
注意: 本章大部分理论内容来自 Hopcroft, J.E., and J.D. Ullman. 自动机理论、语言和计算导论。 Reading, Massachusetts: Addison-Wesley, 1979, 第7章。
艾伦·图灵最初描述的图灵机 (TM) 由一条无限长的磁带、一个有限控制器和一个置于磁带上的读写 (RW) 磁头组成。为了模拟目的,一个 (基本) TM,如下图所示,由一个半无限长的磁带 (用于存储符号) 和一个有限控制器与一个 RW 磁头组成,该磁头可以向右或向左移动。要处理的符号字符串在磁带上左对齐 (在标记磁带开头的特殊符号 '#' 之后),其后是一个不确定的“空白”符号字符串。



图灵机的描述
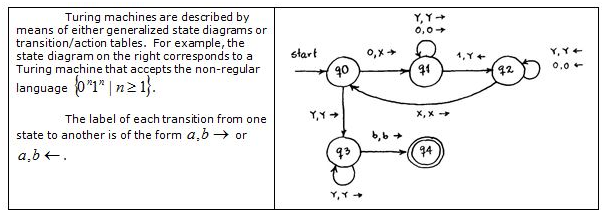
在状态转移的标签中,a 表示 RW 磁头当前位置的输入磁带上的符号,b 表示将替换磁带上 a 的符号,而箭头表示替换发生后 RW 磁头必须移动的方向。
为了模拟目的,TM 的描述可以存储在文本文件中。对于上面的示例状态图,我们可以有以下描述。

请注意,在描述中,输入字母表包含了空白字符,它被写在 "01" 和 "XY" 之间,以便被识别。
在包含状态数量和 TM 字母表的行之后,一系列行描述了每个状态允许的转移。每行以状态名称开头,然后包含形式为
InputSymbol ( NextState ReplacementSymbol DirectionOfMotion ) .
另外请注意,在实际的转移规范中,逗号是可选的分隔符。
TM 描述中的注释
模拟器(稍后讨论)允许在 TM 描述中使用注释。任何以 ";" 开头的行都将被视为注释。此外,在指定状态转移时,可以通过将注释括在 "{" 和 "}" 字符之间来添加注释。此外,空行将被忽略并直接回显到输出。
例如,我将说明一个基本 TM 的设计,该 TM 用于接受由 { 0, 1 } 字母表上的偶数长度回文组成的语言,即集合定义为


通用图灵机模拟器
该模拟器是用 Visual Studio 2010 下的非托管 C++ 编写的,将从顶层函数到底层辅助函数的自顶向下方式进行描述。
包含文件、结构和全局变量
在深入了解模拟器的功能之前,必须提供要使用的包含文件、数据结构和全局变量。它们定义如下。(注释应使其不言自明。)
#include "stdafx.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include <malloc.h>
#include <dos.h>
#include <time.h>
#define nFile 30 // file-name characters
#define nLine 350 // input-line characters
#define nDigits 2 // maximum digits in a decimal number
#define nBdigits 7 // maximum binary digits for decimal numbers
#define nStates 100 // maximum number of states
#define nAlpha 20 // maximum number of alphabet symbols
typedef struct { // structure for transition-matrix entries
int q; // next state
char s, // symbol to write on TM tape
d; // direction of motion of TM read/write head
} TMstruct, *TMstrPtr;
TMstrPtr TMrule[ nStates ][ nAlpha ]; // transition matrix of simulated TM
char binary[ nStates ][ nBdigits + 1 ]; // binary-character string
// representation of states
time_t tStart, tEnd; // start/end nSimSteps to calculate elapsed time
typedef enum
{ number, lparen, rparen, comma,
dash, _q, _b, _l, _r, _char, eol } SymbolType;
int pos, // current scan position in input line
len, // length of input line
numVal, // numeric value of symbolic number
mStates, // number of TM states
mSymbols, // number of TM symbols (including ' ')
state, // global index into TMrule[ state ][ ... ]
nSimSteps; // number of simulation steps
FILE *fp; // pointer to input file stream
SymbolType symbol; // type of symbol scanned
char fileName[ nFile ], // input file name
line[ nLine ], // input line from file
alphabet[ nLine ], // TM alphabet
aChar; // non-special single character
char *errorMsg[ 6 ]
= { "'q'", "number", "'b' or non-special character",
"'('", "'l', 'r' or '-'", "')'" };
主函数
int _tmain(int argc, _TCHAR* argv[])
{
printf( "input file? " );
gets( fileName );
if ( ( fp = fopen( fileName, "r" ) ) == NULL )
{
printf( "\nunable to open file '%s'\n", fileName );
}
else
{
printf( "%s\n", fileName );
printf( "number of simulation steps [0 = indefinite]? " );
scanf( "%d", &nSimSteps );
printf( "%d\n", nSimSteps );
InputTM();
ReportTM();
SimulateTM();
DescribeTM();
FreeMemory();
}
return 0;
}// _tmain
Turing.cpp 的主函数需要两个输入:输入文件的名称和模拟步数。(模拟步数是必需的,因为某些 TM 可能会无限运行。因此,当步数不为 0 时,可用于停止模拟。) Turing.exe 被定义为一个控制台应用程序。如果交互式运行,则必须输入这两个输入。但是,可以使用 I/O 重定向来提供输入。假设我们要模拟一个名为 sampleTM 的 TM,我们可以创建两个文本文件:sampleTM.txt 和 sampleTM_in.txt。文件 sampleTM.txt 应包含以下两行
sampleTM_in.txt 0
而文件 sampleTM_in.txt 应包含 TM 的描述。然后,可以通过命令行提示符使用以下调用启动模拟(请注意重定向字符 "<")
Turing.exe <sampleTM.txt
在获得(并回显)有效输入后,主函数读取 TM 的描述 (InputTM),报告描述以进行验证 (ReportTM),启动模拟 (SimulateTM),生成一个字符串来描述 TM (DescribeTM),以便 TM 可以被另一个 TM 模拟 [稍后详述],并释放所有动态使用的内存 (FreeMemory)。
InputTM
本质上,函数 InputTM 是 TM 描述的普通解析器。它获取 TM 的状态数量和字母表。在初始化将包含 TM 转移规则的数组后,该函数通过为 TM 的每个状态的每个包含转移的行调用辅助函数 NextSymbol 和 TM_P 来解析(通过函数 GetLine 获取)每一行。
void InputTM()
{
int i, j;
GetLine( line );
mStates = atoi( line );
mSymbols = GetLine( alphabet );
for ( i = 0; i < nStates; ++i )
{
for ( j = 0; j < nAlpha; ++j )
{
TMrule[ i ][ j ] = NULL;
}
}
printf( "\n" );
while ( ( len = GetLine( line ) ) != 0 )
{
printf( "%s\n", line );
if ( line[ 0 ] == '*' )
{
break;
}
pos = 0;
if ( pos < len )
{
NextSymbol();
TM_P();
}
}
}// InputTM
GetLine
函数 GetLine 用于跳过注释和为解析转移规则的行数组填充内容。
int GetLine( char line[] )
{
int commentLine = 1;
while ( commentLine && ( fgets( line, nLine, fp ) != NULL) )
{
len = strlen( line ) - 1;
line[ len ] = '\0';
if ( BlankLine( line, len ) )
{
printf( "" );
continue;
}
if ( line[ 0 ] != ';' )
{
commentLine = 0;
}
else printf( "%s\n", line );
}
return len;
}// GetLine
NextSymbol
此函数负责处理输入行的内容。它会跳过空格和注释。它将数字字符串转换为数字,并处理转移规则中的特殊字符。函数 SkipBlanks 和 SkipComment 是不言自明的,此处不作描述。(它们定义在完整的源代码中。) NextSymbol 的参数控制该函数是否解析数字字符串。默认情况下,该函数会解析它们。
void NextSymbol( int scanForNumOK = 1 )
{
// pos < len
char ch;
int i;
SkipBlanks();
SkipComment();
SkipBlanks();
if ( pos < len )
{
ch = line[ pos++ ];
if ( scanForNumOK && isdigit( (int)ch ) )
{
numVal = 0; i = 1;
do {
if ( i < nDigits )
{
numVal = numVal * 10 + ch - '0';
}
ch = line[ pos++ ];
} while ( isdigit( (int)ch ) && pos < len );
symbol = number;
}
else
{
switch ( tolower( ch ) )
{
case '(': symbol = lparen; break;
case ')': symbol = rparen; break;
case ',': symbol = comma; break;
case '-': symbol = dash; break;
case 'q': symbol = _q; break;
case 'b': symbol = _b; ch = ' '; break;
case 'l': symbol = _l; break;
case 'r': symbol = _r; break;
default: symbol = _char; break;
}
aChar = ch;
}
}
else
{
symbol = eol;
}
}// NextSymbol
TM_P
函数 TM_P 通过函数 TM_S 获取 TM 描述行中的起始状态,并通过调用函数 TM_T 来启动该状态的转移规则解析。
void TM_P()
{
TM_S( &state );
TM_T();
}// TM_P
TM_S
函数 TM_S 解析 TM 描述行中的起始状态。预期的格式是 qN,其中 N 表示一个数字。如果解析成功,则调用 NextSymbol 函数,并指示不解析数字;否则,调用 Error 函数以指示语法错误。
void TM_S( int *var )
{
if ( symbol == _q )
{
NextSymbol();
if ( symbol == number )
{
*var = numVal;
NextSymbol( 0 );
}
else Error( 1 );
}
else Error( 0 );
}// TM_S
TM_T
函数 TM_T 递归地解析由函数 TM_S 获取的起始状态的转移规则。根据前面的示例,转移规则的格式为 S(NS RS D),其中 S 代表 RW 磁头上的当前符号,NS 代表下一个状态,RS 代表将要替换 S 的符号,D 代表 RW 磁头替换后必须移动的方向(L 表示左,R 表示右,– 表示不移动)。
void TM_T()
{
char inC, repC, dir;
int nxtQ;
TMstrPtr p;
if ( symbol != eol )
{
if ( symbol == _b || symbol == _char )
{
inC = aChar;
NextSymbol();
if ( symbol == lparen )
{
NextSymbol();
TM_S( &nxtQ );
SkipComma();
if ( symbol == _b || symbol == _char )
{
repC = aChar;
NextSymbol();
SkipComma();
if ( symbol == _l || symbol == _r || symbol == dash )
{
dir = aChar;
p = (TMstrPtr)malloc( sizeof( TMstruct ) );
p->q = nxtQ;
p->s = repC;
p->d = dir;
TMrule[ state ][ CharIndex( inC ) ] = p;
NextSymbol();
if ( symbol == rparen )
{
NextSymbol( 0 );
TM_T();
}
else Error( 5 );
}
else Error( 4 );
}
else Error( 2 );
}
else Error( 3 );
}
else Error( 2 );
}
}// TM_T
ReportTM
一旦 TM 描述被处理完毕,主函数将调用 ReportTM 函数以矩阵形式打印描述,以便用户验证描述是否被正确处理。
void ReportTM()
{
int i, j;
printf( "\nTuring machine: %s\n", fileName );
printf( "%d states; \nalphabet: '%s', %d symbols\n",
mStates, alphabet, mSymbols );
printf( "\ntransition/action matrix:\n\n " );
for ( j = 0; j < mSymbols; ++j )
{
printf( " %c ", EquivalentChar( alphabet[ j ] ) );
}
printf( "\n\n" );
for ( i = 0; i < mStates; ++i )
{
printf( "q%2d ", i );
for ( j = 0; j < mSymbols; ++j )
{
PrintTMstring( TMrule[ i ][ j ] );
}
printf( "\n" );
}
}// ReportTM
函数 EquivalentChar 仅将空格转换为字符 'b'。函数 PrintTMstring 打印一条转移规则,如果没有转移则打印 "/"。这些函数此处不予显示。(同样,提供了完整的源代码。)
SimulateTM
模拟器的核心是函数 SimulateTM。该函数通过逐个处理描述后 '*' 字符后面的输入来执行 TM 描述编码的程序。每个输入都被加载到磁带上,并对磁带上的字符应用 TM 规则。每次应用规则后,都会调用 PrintConfiguration 函数来显示磁带的内容。
void SimulateTM()
{
char tape[ nLine ];
int h, q, n, i, t;
TMstrPtr p;
Dword steps;
time( &tStart );
printf( "\nSimulating turing machine\n" );
while ( ( n = GetLine( tape ) ) > 0 )
{
if ( tape[ 0 ] == '!' ) // terminator for input cases
{
break;
}
printf( "\n" );
for ( i = n; i < nLine - 1; ++i )
{
tape[ i ] = ' ';
}
tape[ nLine - 1 ] = '\0';
t = h = q = 0;
steps = 0L;
while ( q >= 0 )
{
PrintConfiguration( q, tape, h );
p = TMrule[ q ][ CharIndex( tape[ h ] ) ];
if ( p != NULL )
{
++steps;
q = p->q;
tape[ h ] = p->s;
if ( p->d == '-' )
{
break;
}
h += ( tolower( p->d ) == 'r' ) ? 1 : -1;
if ( h < 0 || h == nLine )
{
printf( "illegal head position: %d\n", h );
q = -1;
}
if ( nSimSteps > 0 )
{
++t;
if ( t > nSimSteps )
{
break;
}
}
}
else
{
break;
}
}
PrintConfiguration( q, tape, h );
printf( "\nInput %saccepted\n",
( q == mStates -1 ) ? "" : "not " );
printf( "%lu simulation steps\n", steps );
}
fclose( fp );
time( &tEnd );
ReportElapsedTime();
}// SimulateTM
PrintConfiguration
此函数在每次模拟步骤后打印 TM 的内容。编码 |qN>,其中 N 代表状态编号,指示 RW 磁头的位置。紧跟 '>' 字符的符号是下一个要处理的符号。
void PrintConfiguration( int q, char t[], int h )
{
int i;
char c;
for ( i = 0; i < h; ++i )
{
printf( "%c", t[ i ] );
}
printf( "|q%d>", q );
i = h;
while ( i < len )
{
printf( "%c", t[ i++ ] );
}
while( (c = t[ i++ ]) != ' ' )
{
printf( "%c", c );
}
printf( "\n" );
}// PrintConfiguration
DescribeTM
在 TM 模拟完成后,将调用 DescribeTM 函数来生成并打印一个编码字符串,该字符串描述了 TM,以便它可以被通用图灵机模拟。此时,详细介绍此函数及其辅助函数的工作原理没有意义。一旦在本篇文章后面处理完通用图灵机,我将返回到此函数。现在我转向 TM 模拟的示例。
图灵机模拟示例
为了说明 TM 模拟器的使用,我将展示一些有趣的 TM。本文中描述的所有 TM 的文本文件也已提供。
一个接受非正则语言 0^n1^n 的 TM
TM 比有限自动机优越性的经典例子之一是接受非正则语言的 TM,因为众所周知有限自动机无法处理非正则语言。本例展示了对正则语言 0^n1^n 的处理,其中 '^' 表示逻辑意义上的指数,即多次连接。如前所述,需要两个文件来执行模拟。例如,“驱动”文件将是 0n1n.txt,其内容如下
0n1nTM_in.txt 0
文件 0n1nTM_in.txt 包含 TM 的描述和要处理的输入
;
; 0n1nTM_in.txt
;
; Turing Machine that accepts the non-regular language
; 0^n1^n for n >= 1.
;
5
01 XY
q0 0(q1 X R) Y(q3 Y R)
q1 0(q1 0 R) 1(q2 Y L) Y(q1 Y R)
q2 0(q2 0 L) X(q0 X R) Y(q2 Y L)
q3 Y(q3 Y R) B(q4 B R)
q4
*
00001111
00100
!
两个给定输入的模拟结果如下
;
; 0n1nTM_in.txt
;
; Turing Machine that accepts the non-regular language
; 0^n1^n for n >= 1.
;
q0 0(q1 X R) Y(q3 Y R)
q1 0(q1 0 R) 1(q2 Y L) Y(q1 Y R)
q2 0(q2 0 L) X(q0 X R) Y(q2 Y L)
q3 Y(q3 Y R) B(q4 B R)
q4
*
Turing machine: 0n1nTM_in.txt
5 states;
alphabet: '01 XY', 5 symbols
transition/action matrix:
0 1 b X Y
q 0 q 1, X,R / / / q 3, Y,R
q 1 q 1, 0,R q 2, Y,L / / q 1, Y,R
q 2 q 2, 0,L / / q 0, X,R q 2, Y,L
q 3 / / q 4, b,R / q 3, Y,R
q 4 / / / / /
Simulating turing machine
|q0>00001111
X|q1>0001111
X0|q1>001111
X00|q1>01111
X000|q1>1111
X00|q2>0Y111
X0|q2>00Y111
X|q2>000Y111
|q2>X000Y111
X|q0>000Y111
XX|q1>00Y111
XX0|q1>0Y111
XX00|q1>Y111
XX00Y|q1>111
XX00|q2>YY11
XX0|q2>0YY11
XX|q2>00YY11
X|q2>X00YY11
XX|q0>00YY11
XXX|q1>0YY11
XXX0|q1>YY11
XXX0Y|q1>Y11
XXX0YY|q1>11
XXX0Y|q2>YY1
XXX0|q2>YYY1
XXX|q2>0YYY1
XX|q2>X0YYY1
XXX|q0>0YYY1
XXXX|q1>YYY1
XXXXY|q1>YY1
XXXXYY|q1>Y1
XXXXYYY|q1>1
XXXXYY|q2>YY
XXXXY|q2>YYY
XXXX|q2>YYYY
XXX|q2>XYYYY
XXXX|q0>YYYY
XXXXY|q3>YYY
XXXXYY|q3>YY
XXXXYYY|q3>Y
XXXXYYYY|q3>
XXXXYYYY |q4>
XXXXYYYY |q4>
Input accepted
41 simulation steps
|q0>00100
X|q1>0100
X0|q1>100
X|q2>0Y00
|q2>X0Y00
X|q0>0Y00
XX|q1>Y00
XXY|q1>00
XXY0|q1>0
XXY00|q1>
XXY00|q1>
Input not accepted
9 simulation steps
Elapsed time: 0 seconds
TM description for LCCP UTM:
y0000x0000001X1x000Y011Y1x001000101x0011010Y0x001Y001Y1x010001000x010X000X1x010Y010Y0x011 100 1x011Y011Y1y0
同样,在模拟结束时,会有一个编码字符串描述 TM,以便通用图灵机(出于历史原因,命名为“LCCP UTM”,稍后解释)进行模拟。从模拟结果来看,第一个输入是语言中的一个字符串,而第二个不是。读者可能已经注意到输出文件中没有“回显”模拟器参数(输入文件名和模拟步数)。原因在于输出文件是由我于2002年编写的原始模拟器生成的。对于其余的示例,我将不显示“驱动”文件,也不显示 TM 描述文件,因为模拟器会显示 TM 描述,并且每个模拟的第一个配置都显示要处理的输入。
一个验证括号字符串是否平衡的 TM
input file? BalancedParenthesesTM_in.txt
number of simulation steps [0 = indefinite]? 0
;
; BalancedParenthesesTM_in.txt
;
; Turing Machine to check whether or not a string containing
; left and right parentheses is well-formed, that is,whether
; they can be paired of from inside to outside so that each
; left parenthesis has a right-hand mate.
;
; After Minsky, M. "Computation: Finite and Infinite Machines"
; Prentice-Hall, 1967, pp. 121-122.
;
; A description based on Minsky's is given in Feynman, R.
; "Feynman's Lectures on Computation" Westview, 1996, pp. 71-73.
;
; Due to the way transitions are described (inside parentheses)
; for the simulator, the original problem is modified to use
; square brackets '[' and ']' instead of parentheses.
;
; Input format: A ... <string of square brackets> ... A
;
; NOTE: Even though the processing of all the input cases will
; yield "Input accepted" the contents of the tape will
; indicate with a '1' that the string is well-formed
; and with a '0' that it is not.
;
; Also note that both Minsky and Feynman implicitly assume the
; existence of state q0 below.
q0 A(q1 A R)
q1 A(q3 A L) x(q1 x R) [(q1 [ R) ](q2 x L)
q2 A(q4 0 -) x(q2 x L) [(q1 x R) ](q2 ] L)
q3 A(q4 1 -) x(q3 x L) [(q4 0 -)
q4
*
Turing machine: BalancedParenthesesTM_in.txt
5 states;
alphabet: 'A[]x01', 6 symbols
transition/action matrix:
A [ ] x 0 1
q 0 q 1, A,R / / / / /
q 1 q 3, A,L q 1, [,R q 2, x,L q 1, x,R / /
q 2 q 4, 0,- q 1, x,R q 2, ],L q 2, x,L / /
q 3 q 4, 1,- q 4, 0,- / q 3, x,L / /
q 4 / / / / / /
Simulating turing machine
|q0>AA
A|q1>A
|q3>AA
|q4>1A
Input accepted
3 simulation steps
|q0>A[[[[][]][]]]A
A|q1>[[[[][]][]]]A
A[|q1>[[[][]][]]]A
A[[|q1>[[][]][]]]A
A[[[|q1>[][]][]]]A
A[[[[|q1>][]][]]]A
A[[[|q2>[x[]][]]]A
A[[[x|q1>x[]][]]]A
A[[[xx|q1>[]][]]]A
A[[[xx[|q1>]][]]]A
A[[[xx|q2>[x][]]]A
A[[[xxx|q1>x][]]]A
A[[[xxxx|q1>][]]]A
A[[[xxx|q2>xx[]]]A
A[[[xx|q2>xxx[]]]A
A[[[x|q2>xxxx[]]]A
A[[[|q2>xxxxx[]]]A
A[[|q2>[xxxxx[]]]A
A[[x|q1>xxxxx[]]]A
A[[xx|q1>xxxx[]]]A
A[[xxx|q1>xxx[]]]A
A[[xxxx|q1>xx[]]]A
A[[xxxxx|q1>x[]]]A
A[[xxxxxx|q1>[]]]A
A[[xxxxxx[|q1>]]]A
A[[xxxxxx|q2>[x]]A
A[[xxxxxxx|q1>x]]A
A[[xxxxxxxx|q1>]]A
A[[xxxxxxx|q2>xx]A
A[[xxxxxx|q2>xxx]A
A[[xxxxx|q2>xxxx]A
A[[xxxx|q2>xxxxx]A
A[[xxx|q2>xxxxxx]A
A[[xx|q2>xxxxxxx]A
A[[x|q2>xxxxxxxx]A
A[[|q2>xxxxxxxxx]A
A[|q2>[xxxxxxxxx]A
A[x|q1>xxxxxxxxx]A
A[xx|q1>xxxxxxxx]A
A[xxx|q1>xxxxxxx]A
A[xxxx|q1>xxxxxx]A
A[xxxxx|q1>xxxxx]A
A[xxxxxx|q1>xxxx]A
A[xxxxxxx|q1>xxx]A
A[xxxxxxxx|q1>xx]A
A[xxxxxxxxx|q1>x]A
A[xxxxxxxxxx|q1>]A
A[xxxxxxxxx|q2>xxA
A[xxxxxxxx|q2>xxxA
A[xxxxxxx|q2>xxxxA
A[xxxxxx|q2>xxxxxA
A[xxxxx|q2>xxxxxxA
A[xxxx|q2>xxxxxxxA
A[xxx|q2>xxxxxxxxA
A[xx|q2>xxxxxxxxxA
A[x|q2>xxxxxxxxxxA
A[|q2>xxxxxxxxxxxA
A|q2>[xxxxxxxxxxxA
Ax|q1>xxxxxxxxxxxA
Axx|q1>xxxxxxxxxxA
Axxx|q1>xxxxxxxxxA
Axxxx|q1>xxxxxxxxA
Axxxxx|q1>xxxxxxxA
Axxxxxx|q1>xxxxxxA
Axxxxxxx|q1>xxxxxA
Axxxxxxxx|q1>xxxxA
Axxxxxxxxx|q1>xxxA
Axxxxxxxxxx|q1>xxA
Axxxxxxxxxxx|q1>xA
Axxxxxxxxxxxx|q1>A
Axxxxxxxxxxx|q3>xA
Axxxxxxxxxx|q3>xxA
Axxxxxxxxx|q3>xxxA
Axxxxxxxx|q3>xxxxA
Axxxxxxx|q3>xxxxxA
Axxxxxx|q3>xxxxxxA
Axxxxx|q3>xxxxxxxA
Axxxx|q3>xxxxxxxxA
Axxx|q3>xxxxxxxxxA
Axx|q3>xxxxxxxxxxA
Ax|q3>xxxxxxxxxxxA
A|q3>xxxxxxxxxxxxA
|q3>AxxxxxxxxxxxxA
|q4>1xxxxxxxxxxxxA
Input accepted
83 simulation steps

Elapsed time: 0 seconds
TM description for LCCP UTM:
y0000x000A001A1x001A011A0x001[001[1x001]010x0x001x001x1x010A10001x010[001x1x010]010]0x010x010x0x011A10011x011[10001x011x011x0y0
一个生成二进制数的 TM
这是需要模拟器第二个输入(模拟步数)的例子。没有这个参数,这个 TM 将无限运行。生成的二进制数以粗体显示。
input file? BinNumGenTM_in.txt
number of simulation steps [0 = indefinite]? 60
;
; BinNumGenTM_in.txt
;
; Turing Machine to Generate Binary Numbers
;
q0 0(q0 0 R) 1(q1 1 L)
q1 0(q0 1 R) 1(q1 0 L)
*
Turing machine: BinNumGenTM_in.txt
2 states;
alphabet: '01', 2 symbols
transition/action matrix:
0 1
q 0 q 0, 0,R q 1, 1,L
q 1 q 0, 1,R q 1, 0,L
Simulating turing machine
|q0>0000000010000
0|q0>000000010000
00|q0>00000010000
000|q0>0000010000
0000|q0>000010000
00000|q0>00010000
000000|q0>0010000
0000000|q0>010000
00000000|q0>10000
0000000|q1>010000
00000001|q0>10000
0000000|q1>110000
000000|q1>0010000
0000001|q0>010000
00000010|q0>10000
0000001|q1>010000
00000011|q0>10000
0000001|q1>110000
000000|q1>1010000
00000|q1>00010000
000001|q0>0010000
0000010|q0>010000
00000100|q0>10000
0000010|q1>010000
00000101|q0>10000
0000010|q1>110000
000001|q1>0010000
0000011|q0>010000
00000110|q0>10000
0000011|q1>010000
00000111|q0>10000
0000011|q1>110000
000001|q1>1010000
00000|q1>10010000
0000|q1>000010000
00001|q0>00010000
000010|q0>0010000
0000100|q0>010000
00001000|q0>10000
0000100|q1>010000
00001001|q0>10000
0000100|q1>110000
000010|q1>0010000
0000101|q0>010000
00001010|q0>10000
0000101|q1>010000
00001011|q0>10000
0000101|q1>110000
000010|q1>1010000
00001|q1>00010000
000011|q0>0010000
0000110|q0>010000
00001100|q0>10000
0000110|q1>010000
00001101|q0>10000
0000110|q1>110000
000011|q1>0010000
0000111|q0>010000
00001110|q0>10000
0000111|q1>010000
00001111|q0>10000
0000111|q1>110000
Input accepted
61 simulation steps
Elapsed time: 0 seconds
TM description for LCCP UTM:
y00x00001x01110x10011x11100y0
一个识别回文的 TM
这个例子说明了在 TM 描述中使用注释。
input file? GpalindromeTM_in.txt
number of simulation steps [0 = indefinite]? 0
; GpalindromeTM_in.txt
;
; Design a TM to recognize "generalized" palindromes, that is, strings that read
; the same forward and backward if intervening blank spaces are ignored.
;
; The test strings are enclosed by the '.' character at the beginning and the end.
;
{ find first non-'.' on the right } q0 .(q1 . R)
{ dispatch to separate states on 0/1 } q1 b(q1 . R) 0(q2 . R) 1(q5 . R) .(q7 . R)
{ seen 0, find '.' on the right } q2 b(q2 b R) 0(q2 0 R) 1(q2 1 R) .(q3 . L)
{ if matching 0, erase and repeat } q3 b(q3 . L) 0(q4 . L) .(q7 . R)
{ find '.' on the left } q4 b(q4 b L) 0(q4 0 L) 1(q4 1 L) .(q1 . R)
{ seen 1, find '.' on the right } q5 b(q5 b R) 0(q5 0 R) 1(q5 1 R) .(q6 . L)
{ if matching 1, erase and repeat } q6 b(q6 . L) 1(q4 . L) b(q7 . R)
{ no more non-'.' characters, accept } q7
*
Turing machine: GpalindromeTM_in.txt
8 states;
alphabet: '. 01', 4 symbols
transition/action matrix:
. b 0 1
q 0 q 1, .,R / / /
q 1 q 7, .,R q 1, .,R q 2, .,R q 5, .,R
q 2 q 3, .,L q 2, b,R q 2, 0,R q 2, 1,R
q 3 q 7, .,R q 3, .,L q 4, .,L /
q 4 q 1, .,R q 4, b,L q 4, 0,L q 4, 1,L
q 5 q 6, .,L q 5, b,R q 5, 0,R q 5, 1,R
q 6 / q 7, .,R / q 4, .,L
q 7 / / / /
Simulating turing machine
|q0>.0 01 10 0.
.|q1>0 01 10 0.
..|q2> 01 10 0.
.. |q2>01 10 0.
.. 0|q2>1 10 0.
.. 01|q2> 10 0.
.. 01 |q2> 10 0.
.. 01 |q2>10 0.
.. 01 1|q2>0 0.
.. 01 10|q2> 0.
.. 01 10 |q2> 0.
.. 01 10 |q2> 0.
.. 01 10 |q2>0.
.. 01 10 0|q2>.
.. 01 10 |q3>0.
.. 01 10 |q4> ..
.. 01 10 |q4> ..
.. 01 10|q4> ..
.. 01 1|q4>0 ..
.. 01 |q4>10 ..
.. 01 |q4> 10 ..
.. 01|q4> 10 ..
.. 0|q4>1 10 ..
.. |q4>01 10 ..
..|q4> 01 10 ..
.|q4>. 01 10 ..
..|q1> 01 10 ..
...|q1>01 10 ..
....|q2>1 10 ..
....1|q2> 10 ..
....1 |q2> 10 ..
....1 |q2>10 ..
....1 1|q2>0 ..
....1 10|q2> ..
....1 10 |q2> ..
....1 10 |q2> ..
....1 10 |q2>..
....1 10 |q3> ..
....1 10 |q3> ...
....1 10|q3> ....
....1 1|q3>0.....
....1 |q4>1......
....1 |q4> 1......
....1|q4> 1......
....|q4>1 1......
...|q4>.1 1......
....|q1>1 1......
.....|q5> 1......
..... |q5> 1......
..... |q5>1......
..... 1|q5>......
..... |q6>1......
..... |q4> .......
.....|q4> .......
....|q4>. .......
.....|q1> .......
......|q1> .......
.......|q1>.......
........|q7>......
........|q7>......
Input accepted
58 simulation steps
|q0>.1 0 1 0 1 0.
.|q1>1 0 1 0 1 0.
..|q5> 0 1 0 1 0.
.. |q5>0 1 0 1 0.
.. 0|q5> 1 0 1 0.
.. 0 |q5>1 0 1 0.
.. 0 1|q5> 0 1 0.
.. 0 1 |q5>0 1 0.
.. 0 1 0|q5> 1 0.
.. 0 1 0 |q5>1 0.
.. 0 1 0 1|q5> 0.
.. 0 1 0 1 |q5>0.
.. 0 1 0 1 0|q5>.
.. 0 1 0 1 |q6>0.
.. 0 1 0 1 |q6>0.
Input not accepted
13 simulation steps
Elapsed time: 0 seconds
TM description for LCCP UTM:
y0000x000.001.1x001.111.1x001 001.1x0010010.1x0011101.1x010.011.0x010 010 1x010001001x010101011x011.111.1x011 011.0x0110100.0x100.001.1x100 100 0x100010000x100110010x101.110.0x101 101 1x101010101x101110111x110 111.1x1101100.0y0
一个以一元格式乘两个数的 TM

这个例子来自 Marvin Minsky 的书《计算:有限与无限机器》(Englewood Cliffs, N.J.: Prentice Hall, 1967, p. 125)。TM 的状态图如下(为方便起见,我重命名了状态以适应模拟器的格式)
以下是两次模拟,一次是 3x2,一次是 2x4。参数和结果以粗体显示。
input file? mXnTM_in.txt
number of simulation steps [0 = indefinite]? 0
;
; mXnTM_in.txt
;
; Turing Machine to multiply two unary numbers.
;
; Adapted from Minsky, M. "Computation: Finite and Infinite Machines"
; Prentice-Hall, 1967, p. 125
;
; Input format: ...A...m...y...n...A00000000000000000000
; ^ plenty of 0s to hold the result
;
; Output: ...A00...00y x^n Ax... (x^(mn))
q0 0(q0 0 R) A(q0 A R) 1(q0 1 R) y(q1 y L)
q1 1(q2 0 R) 0(q1 0 L) A(q5 A -)
q2 x(q2 1 R) A(q3 A L) y(q2 y R) 1(q2 1 R) 0(q2 0 R)
q3 y(q1 y L) 1(q4 x R) A(q3 A L) x(q3 x L)
q4 0(q3 x L) A(q4 A R) 1(q4 1 R) x(q4 x R)
q5
*
Turing machine: mXnTM_in.txt
6 states;
alphabet: '01Ayx', 5 symbols
transition/action matrix:
0 1 A y x
q 0 q 0, 0,R q 0, 1,R q 0, A,R q 1, y,L /
q 1 q 1, 0,L q 2, 0,R q 5, A,- / /
q 2 q 2, 0,R q 2, 1,R q 3, A,L q 2, y,R q 2, 1,R
q 3 / q 4, x,R q 3, A,L q 1, y,L q 3, x,L
q 4 q 3, x,L q 4, 1,R q 4, A,R / q 4, x,R
q 5 / / / / /
Simulating turing machine
|q0>00A111y11A00000000
0|q0>0A111y11A00000000
00|q0>A111y11A00000000
00A|q0>111y11A00000000
00A1|q0>11y11A00000000
00A11|q0>1y11A00000000
00A111|q0>y11A00000000
00A11|q1>1y11A00000000
00A110|q2>y11A00000000
00A110y|q2>11A00000000
00A110y1|q2>1A00000000
00A110y11|q2>A00000000
00A110y1|q3>1A00000000
00A110y1x|q4>A00000000
00A110y1xA|q4>00000000
00A110y1x|q3>Ax0000000
00A110y1|q3>xAx0000000
00A110y|q3>1xAx0000000
00A110yx|q4>xAx0000000
00A110yxx|q4>Ax0000000
00A110yxxA|q4>x0000000
00A110yxxAx|q4>0000000
00A110yxxA|q3>xx000000
00A110yxx|q3>Axx000000
00A110yx|q3>xAxx000000
00A110y|q3>xxAxx000000
00A110|q3>yxxAxx000000
00A11|q1>0yxxAxx000000
00A1|q1>10yxxAxx000000
00A10|q2>0yxxAxx000000
00A100|q2>yxxAxx000000
00A100y|q2>xxAxx000000
00A100y1|q2>xAxx000000
00A100y11|q2>Axx000000
00A100y1|q3>1Axx000000
00A100y1x|q4>Axx000000
00A100y1xA|q4>xx000000
00A100y1xAx|q4>x000000
00A100y1xAxx|q4>000000
00A100y1xAx|q3>xx00000
00A100y1xA|q3>xxx00000
00A100y1x|q3>Axxx00000
00A100y1|q3>xAxxx00000
00A100y|q3>1xAxxx00000
00A100yx|q4>xAxxx00000
00A100yxx|q4>Axxx00000
00A100yxxA|q4>xxx00000
00A100yxxAx|q4>xx00000
00A100yxxAxx|q4>x00000
00A100yxxAxxx|q4>00000
00A100yxxAxx|q3>xx0000
00A100yxxAx|q3>xxx0000
00A100yxxA|q3>xxxx0000
00A100yxx|q3>Axxxx0000
00A100yx|q3>xAxxxx0000
00A100y|q3>xxAxxxx0000
00A100|q3>yxxAxxxx0000
00A10|q1>0yxxAxxxx0000
00A1|q1>00yxxAxxxx0000
00A|q1>100yxxAxxxx0000
00A0|q2>00yxxAxxxx0000
00A00|q2>0yxxAxxxx0000
00A000|q2>yxxAxxxx0000
00A000y|q2>xxAxxxx0000
00A000y1|q2>xAxxxx0000
00A000y11|q2>Axxxx0000
00A000y1|q3>1Axxxx0000
00A000y1x|q4>Axxxx0000
00A000y1xA|q4>xxxx0000
00A000y1xAx|q4>xxx0000
00A000y1xAxx|q4>xx0000
00A000y1xAxxx|q4>x0000
00A000y1xAxxxx|q4>0000
00A000y1xAxxx|q3>xx000
00A000y1xAxx|q3>xxx000
00A000y1xAx|q3>xxxx000
00A000y1xA|q3>xxxxx000
00A000y1x|q3>Axxxxx000
00A000y1|q3>xAxxxxx000
00A000y|q3>1xAxxxxx000
00A000yx|q4>xAxxxxx000
00A000yxx|q4>Axxxxx000
00A000yxxA|q4>xxxxx000
00A000yxxAx|q4>xxxx000
00A000yxxAxx|q4>xxx000
00A000yxxAxxx|q4>xx000
00A000yxxAxxxx|q4>x000
00A000yxxAxxxxx|q4>000
00A000yxxAxxxx|q3>xx00
00A000yxxAxxx|q3>xxx00
00A000yxxAxx|q3>xxxx00
00A000yxxAx|q3>xxxxx00
00A000yxxA|q3>xxxxxx00
00A000yxx|q3>Axxxxxx00
00A000yx|q3>xAxxxxxx00
00A000y|q3>xxAxxxxxx00
00A000|q3>yxxAxxxxxx00
00A00|q1>0yxxAxxxxxx00
00A0|q1>00yxxAxxxxxx00
00A|q1>000yxxAxxxxxx00
00|q1>A000yxxAxxxxxx00
00|q5>A000yxxAxxxxxx00
Input accepted
101 simulation steps
|q0>00A11y1111A0000000000
0|q0>0A11y1111A0000000000
00|q0>A11y1111A0000000000
00A|q0>11y1111A0000000000
00A1|q0>1y1111A0000000000
00A11|q0>y1111A0000000000
00A1|q1>1y1111A0000000000
00A10|q2>y1111A0000000000
00A10y|q2>1111A0000000000
00A10y1|q2>111A0000000000
00A10y11|q2>11A0000000000
00A10y111|q2>1A0000000000
00A10y1111|q2>A0000000000
00A10y111|q3>1A0000000000
00A10y111x|q4>A0000000000
00A10y111xA|q4>0000000000
00A10y111x|q3>Ax000000000
00A10y111|q3>xAx000000000
00A10y11|q3>1xAx000000000
00A10y11x|q4>xAx000000000
00A10y11xx|q4>Ax000000000
00A10y11xxA|q4>x000000000
00A10y11xxAx|q4>000000000
00A10y11xxA|q3>xx00000000
00A10y11xx|q3>Axx00000000
00A10y11x|q3>xAxx00000000
00A10y11|q3>xxAxx00000000
00A10y1|q3>1xxAxx00000000
00A10y1x|q4>xxAxx00000000
00A10y1xx|q4>xAxx00000000
00A10y1xxx|q4>Axx00000000
00A10y1xxxA|q4>xx00000000
00A10y1xxxAx|q4>x00000000
00A10y1xxxAxx|q4>00000000
00A10y1xxxAx|q3>xx0000000
00A10y1xxxA|q3>xxx0000000
00A10y1xxx|q3>Axxx0000000
00A10y1xx|q3>xAxxx0000000
00A10y1x|q3>xxAxxx0000000
00A10y1|q3>xxxAxxx0000000
00A10y|q3>1xxxAxxx0000000
00A10yx|q4>xxxAxxx0000000
00A10yxx|q4>xxAxxx0000000
00A10yxxx|q4>xAxxx0000000
00A10yxxxx|q4>Axxx0000000
00A10yxxxxA|q4>xxx0000000
00A10yxxxxAx|q4>xx0000000
00A10yxxxxAxx|q4>x0000000
00A10yxxxxAxxx|q4>0000000
00A10yxxxxAxx|q3>xx000000
00A10yxxxxAx|q3>xxx000000
00A10yxxxxA|q3>xxxx000000
00A10yxxxx|q3>Axxxx000000
00A10yxxx|q3>xAxxxx000000
00A10yxx|q3>xxAxxxx000000
00A10yx|q3>xxxAxxxx000000
00A10y|q3>xxxxAxxxx000000
00A10|q3>yxxxxAxxxx000000
00A1|q1>0yxxxxAxxxx000000
00A|q1>10yxxxxAxxxx000000
00A0|q2>0yxxxxAxxxx000000
00A00|q2>yxxxxAxxxx000000
00A00y|q2>xxxxAxxxx000000
00A00y1|q2>xxxAxxxx000000
00A00y11|q2>xxAxxxx000000
00A00y111|q2>xAxxxx000000
00A00y1111|q2>Axxxx000000
00A00y111|q3>1Axxxx000000
00A00y111x|q4>Axxxx000000
00A00y111xA|q4>xxxx000000
00A00y111xAx|q4>xxx000000
00A00y111xAxx|q4>xx000000
00A00y111xAxxx|q4>x000000
00A00y111xAxxxx|q4>000000
00A00y111xAxxx|q3>xx00000
00A00y111xAxx|q3>xxx00000
00A00y111xAx|q3>xxxx00000
00A00y111xA|q3>xxxxx00000
00A00y111x|q3>Axxxxx00000
00A00y111|q3>xAxxxxx00000
00A00y11|q3>1xAxxxxx00000
00A00y11x|q4>xAxxxxx00000
00A00y11xx|q4>Axxxxx00000
00A00y11xxA|q4>xxxxx00000
00A00y11xxAx|q4>xxxx00000
00A00y11xxAxx|q4>xxx00000
00A00y11xxAxxx|q4>xx00000
00A00y11xxAxxxx|q4>x00000
00A00y11xxAxxxxx|q4>00000
00A00y11xxAxxxx|q3>xx0000
00A00y11xxAxxx|q3>xxx0000
00A00y11xxAxx|q3>xxxx0000
00A00y11xxAx|q3>xxxxx0000
00A00y11xxA|q3>xxxxxx0000
00A00y11xx|q3>Axxxxxx0000
00A00y11x|q3>xAxxxxxx0000
00A00y11|q3>xxAxxxxxx0000
00A00y1|q3>1xxAxxxxxx0000
00A00y1x|q4>xxAxxxxxx0000
00A00y1xx|q4>xAxxxxxx0000
00A00y1xxx|q4>Axxxxxx0000
00A00y1xxxA|q4>xxxxxx0000
00A00y1xxxAx|q4>xxxxx0000
00A00y1xxxAxx|q4>xxxx0000
00A00y1xxxAxxx|q4>xxx0000
00A00y1xxxAxxxx|q4>xx0000
00A00y1xxxAxxxxx|q4>x0000
00A00y1xxxAxxxxxx|q4>0000
00A00y1xxxAxxxxx|q3>xx000
00A00y1xxxAxxxx|q3>xxx000
00A00y1xxxAxxx|q3>xxxx000
00A00y1xxxAxx|q3>xxxxx000
00A00y1xxxAx|q3>xxxxxx000
00A00y1xxxA|q3>xxxxxxx000
00A00y1xxx|q3>Axxxxxxx000
00A00y1xx|q3>xAxxxxxxx000
00A00y1x|q3>xxAxxxxxxx000
00A00y1|q3>xxxAxxxxxxx000
00A00y|q3>1xxxAxxxxxxx000
00A00yx|q4>xxxAxxxxxxx000
00A00yxx|q4>xxAxxxxxxx000
00A00yxxx|q4>xAxxxxxxx000
00A00yxxxx|q4>Axxxxxxx000
00A00yxxxxA|q4>xxxxxxx000
00A00yxxxxAx|q4>xxxxxx000
00A00yxxxxAxx|q4>xxxxx000
00A00yxxxxAxxx|q4>xxxx000
00A00yxxxxAxxxx|q4>xxx000
00A00yxxxxAxxxxx|q4>xx000
00A00yxxxxAxxxxxx|q4>x000
00A00yxxxxAxxxxxxx|q4>000
00A00yxxxxAxxxxxx|q3>xx00
00A00yxxxxAxxxxx|q3>xxx00
00A00yxxxxAxxxx|q3>xxxx00
00A00yxxxxAxxx|q3>xxxxx00
00A00yxxxxAxx|q3>xxxxxx00
00A00yxxxxAx|q3>xxxxxxx00
00A00yxxxxA|q3>xxxxxxxx00
00A00yxxxx|q3>Axxxxxxxx00
00A00yxxx|q3>xAxxxxxxxx00
00A00yxx|q3>xxAxxxxxxxx00
00A00yx|q3>xxxAxxxxxxxx00
00A00y|q3>xxxxAxxxxxxxx00
00A00|q3>yxxxxAxxxxxxxx00
00A0|q1>0yxxxxAxxxxxxxx00
00A|q1>00yxxxxAxxxxxxxx00
00|q1>A00yxxxxAxxxxxxxx00
00|q5>A00yxxxxAxxxxxxxx00
Input accepted
147 simulation steps
Elapsed time: 0 seconds
TM description for LCCP UTM:
y0000x000000001x000100011x000A000A1x000y001y0x001000100x001101001x001A101A1x010001001x010101011x010A011A0x010y010y1x010x01011x0111100x1x011A011A0x011y001y0x011x011x0x1000011x0x100110011x100A100A1x100x100x1y0
前面的 TM 示例说明了模拟器的操作。再次强调,我运行过的所有 TM 的源文件都已提供。现在我转向 Marvin Minsky 对通用图灵机的描述。
“计算机架构101”游戏
除了图灵在停机问题不可判定的方面做出杰出贡献之外,他还提供了一个通用机器 (UM) 的构造性证明,该机器可以模拟任何特定 TM 的操作。因此,UTM 是任何通用数字计算机的数学模型。图灵对计算机科学领域的贡献应该考虑到,他的模型比冯·诺依曼意义上的实际、存储程序、通用计算机早了十多年。
据我所知,已故的 Marvin Minsky 是少数(如果不是图灵之外唯一的)提供精确、简洁、完整且可用的 UTM 作为 TM 描述的作者之一。(Minsky, M. L. 计算:有限与无限机器。 Englewood Cliffs, N.J.: Prentice-Hall, 1967, pp. 137-143。) 不幸的是,Minsky 之后的自动机理论教科书中几乎没有转载或引用他的 UTM。令我惊喜的是,它被已故的 Richard Feynman 转录了。(Hey, T., and R.W. Allen, Eds. Feynman计算讲义。 Westview, 1999, pp. 75-80。) 尽管他说他的讨论紧密跟随 Minsky 的,Feynman 并没有超越他。问题是 Minsky 的状态图忽略了“默认”操作细节,例如当磁带上的符号不是机器在特定状态下所期望的时该怎么做。Feynman 清楚地认识到这一点,因为在某个地方(参考文献的第79页)他告诉他的读者“[h]ave fun figuring out how it works!” 关于图灵的论文,Martin Davis 说:“这是一篇精彩的论文,但读者应该注意,许多技术细节如给出那样是错误的。” (Davis, M, Ed., 不可判定性:关于不可判定命题、不可解问题和可计算函数的基礎论文,Raven Press, 1965, p. 115。) Charles Petzold 费尽心机纠正了图灵的错误。(Petzold, C., The Annotated Turing, Wiley Publishing, Inc., 2008, pp. 143-161。)
因为我认为 UTM 是一个太重要的概念,不能仅仅作为一个有趣的数学模型,所以我将本节专门用于 Minsky UTM 的设计、实现和模拟。然后,我将使用它来模拟一个特定的 TM。
UTM 将一个特定 TM \(T\) 的描述以及 \(T\) 操作的伪磁带内容作为输入 (在其磁带上)。通过跟踪 \(T\) 的当前状态和其 RW 磁头当前扫描的符号,UTM 可以模拟其操作。TM 的每个状态都由五元组 \(Q_i S_j Q_k S_l D_m\)唯一指定,或者用文字来说
<present state, present symbol, next state, next symbol, direction of motion of the RW head>.
UTM 磁带内容
UTM 的磁带被分成几个部分。如稍后所述,每个部分都以一个特殊标记符号开头。下图说明了 UTM 磁带。

在上图中,\(T\) 的伪磁带跨越从 UTM 磁带开头到包含 \(q_T\) 的第一个单元之前的单元 (或方格)。在伪磁带中,\(h\) 表示机器 \(T\) 的磁头位置,在该位置扫描了符号 \(S_T\)。
用于编码图灵机五元组的二进制表示法
将要由 UTM 模拟的 TM (\(T\)) 的五元组使用以下标准表示法进行编码。

受限 (二进制) 四状态 TM 的示例编码如下
x0010110x1011101x1100000y
图灵机状态在伪磁带与其描述之间的编码
由 UTM 模拟的 TM 的状态(当前状态 [\(q_T\)]、扫描符号 [\(s_T\)])被包围在特殊符号 y 和 x 之间,如下所示。请注意,符号 y 标记 TM 伪磁带的末尾,而符号 x 标记描述 TM 的五元组的开头。右侧进一步出现的 x 分隔五元组。最后一个五元组后是符号 y 和一个 0。(参见 Minsky, M. 计算:有限与无限机器。 Englewood Cliffs, N.J.: Prentice-Hall, 1967, p. 144。) 模拟四状态 TM 的 UTM 磁带的示例如下

在上磁带中,当前状态为 10,在 \(h\) 处扫描的符号为 1。在所有模拟中,h 位于伪磁带的第一个单元,初始状态为 \(Q_0\),扫描的符号为 0。
定位、复制、清理、执行 (LCCP) UTM
我认为 Minsky 对 UTM 的定义之美在于他将其分解为四个子程序,这些子程序本身可以实现为特定的 TM!Minsky 的 UTM 状态图如下。(Minsky, M.L. 计算:有限与无限机器。Englewood Cliffs, N.J.: Prentice-Hall, 1967, p. 142。)

定位。 向右搜索,查找第一个与“机器状态”区域中表示的相匹配的状态-符号对。沿途将 0 变为 a,1 变为 c。找到所需的对(也将其数字变为 a 和 c)后,返回最左边的 x。(如果找不到对,则模拟 T 被中止。) 从初始磁带到成功搜索结束时的磁带的转换如下所示。

复制。 从最左边的 x 开始,向右移动,直到越过最后一个 a 或 c,并首次扫描到某些 0 和 1。这些数字描述了新状态 \(Q_k\),必须最终在位置 h 打印的新符号 \(S_l\),以及移动方向 \(D_m\)。将 0 变为 a,1 变为 c,将表示 \(Q_k\) 和 \(S_l\) 的 0 和 1 复制到机器状态区域;不要将 \(D_m\) 放在磁带上,而是记住它。

清理。 向左移动直到到达 h。擦除 h,并将 (临时) 记住的方向 \(D_m\) 的编码 (a 或 c) 放在它的位置。向右移动,并将所有 a 和 c 更改为 0 和 1,除了 h 的旧位置中的 a 或 c,它现在代表 \(D_m\)。移动到最左边的 x 的正左边。擦除那里的 \(S_l\),记住它,然后将 (临时) s 放在它的位置。

(实际上,磁头应该扫描 s 左边的 1,但我引用的是 Minsky 的描述。)
执行。 向左移动直到找到代表 \(T\) 应该移动的方向 \(D_m\) 的 a 或 c。将 \(S_l\) (0 或 1) 放在 a 或 c 的位置,并根据 \(D_m\) 是 a 还是 c 向左或向右移动一个方格。读取新磁带位置的符号,记住它,并将其放在 h 的位置。向右移动直到找到 s。将 s 替换为记住的符号,使用 a 表示 0,c 表示 1。返回定位。

回到模拟器
现在是回顾模拟器函数 DescribeTM 操作的合适时机。此函数生成 TM 的描述,该描述适合由 LCCP UTM 处理。
void DescribeTM()
{
int i, j;
printf( "\nTM description for LCCP UTM:\n\n" );
GenerateBinaryStates();
printf( "y%s0", binary[ 0 ] ); // Initial state of TM and symbol "scanned"
//printf( "\n" );
for ( i = 0; i < mStates; ++i )
{
for ( j = 0; j < mSymbols; ++j )
{
PrintQuintuple( i, j, TMrule[ i ][ j ] );
}
}
printf( "y0\n" );
}// DescribeTM
函数 GenerateBinaryStates 为 LCCP UTM 生成描述 TM 的状态。
void GenerateBinaryStates()
{
int i, j, k, nBits = Log2( mStates );
for ( i = 0; i < mStates; ++i )
{
binary[ i ][ nBits ] = '\0';
k = i;
for ( j = nBits - 1; -1 < j; --j )
{
binary[ i ][ j ] = (k & 1) ? '1' : '0';
k >>= 1;
}
}
}// GenerateBinaryStates
函数 Log2 计算状态数量的以 2 为底的对数,以获得在五元组中编码状态所需的位数。
int Log2( int n )
{
int nBits = 1, Pof2 = 2;
while ( Pof2 < n )
{
Pof2 <<= 1;
++nBits;
}
return nBits;
}// Log2
函数 PrintQuintuple 以 LCCP UTM 模拟 TM 所需的格式打印一个五元组。
void PrintQuintuple( int i, int j, TMstrPtr p )
{
if ( p != NULL )
{
printf( "x%s%c%s%c%c",
binary[ i ], alphabet[ j ],
binary[ p->q ], p->s, (p->d == 'L') ? '0' : '1' );
}
}// PrintQuintuple
将 LCCP UTM 实现为 TM
毫不奇怪,这个 LCCP UTM (由我命名以纪念 Minsky 的杰作) 可以像任何 TM 一样合成以解决特定问题。LCCP UTM 的每个阶段都将被合成并用模拟简单的 2 状态 TM 以生成二进制数的示例来说明。这个永不停止的 TM 的转移表是

其用于 LCCP UTM 模拟的编码是 0h0010000y00x00001x01110x10011x11100y0。
LCCP UTM 的定位阶段
向右搜索,查找第一个与“机器状态”区域中表示的相匹配的状态-符号对。沿途将 0 变为 a,1 变为 c。找到所需的对(也将其数字变为 a 和 c)后,返回最左边的 x。(如果找不到对,则模拟 T 被中止。)
q0 find leftmost x
q1 scan machine condition, replacing 0/1 by a/c
q2 parse and restore digit of machine condition
q3 digit = 0, skip rest of machine condition until finding x
abort if finding rightmost y;
q4 digit = 1, skip rest of machine condition until finding x
abort if finding rightmost y;
q5 look for 0__ in TM description
q6 look for 1__ in TM description
q7 0__ or 1__ found, go to scan next digit of machine condition
q8 1__/0__ found when looking for 0__/1__, wipe out useless entry
(replace 0/1 by a/c) until finding x for next instruction
q9 look for 'y' on left, replacing 0/1 by a/c, re-start parse


LCCP UTM 的复制阶段
从最左边的 x 开始,向右移动,直到越过最后一个 a 或 c,并首次扫描到某些 0 和 1。这些数字描述了新状态 \(Q_k\),必须最终在位置 h 打印的新符号 \(S_l\),以及移动方向 \(D_m\)。将 0 变为 a,1 变为 c,将表示 \(Q_k\) 和 \(S_l\) 的 0 和 1 复制到机器状态区域;不要将 \(D_m\) 放在磁带上,而是记住它。
machine condition located in TM description
q10 find 0/1, replacing by a/c
q11 0 found, find y on left to write "0" (ya__)
q12 1 found, find y on left to write "1" (yc__)
q13 find 0 or 1 on the right, write "0", that is, 'a'
if x found, direction of head motion is 0 = L
q14 find 0 or 1 on the right, write "1", that is, 'c'
if x found, direction of head motion is 1 = R
q15 find x on the right to repeat the copy process


LCCP UTM 的清理阶段
向左移动直到到达 h。擦除 h,并将 (临时) 记住的方向 \(D_m\) 的编码 (a 或 c) 打印在它的位置。向右移动,并将所有 a 和 c 更改为 0 和 1,除了 h 的旧位置中的 a 或 c,它现在代表 \(D_m\)。移动到最左边的 x 的正左边。擦除那里的 \(S_l\),记住它,然后将 (临时) s 放在它的位置。
q16 x found on right, "0" written last = direction is L
find h on left, replace with 'a'
q17 x found on right, "1" written last = direction is R
find h on left, replace with 'c'
q18 restore QtSt region, replacing a/c by 0/1,
until finding leftmost x
q19 restore TM description, replacing a/c by 0/1
q20 find left y
q21 find leftmost x
q22 put 's' temporarily to the immediate left of x


LCCP UTM 的执行阶段
向左移动直到找到代表 \(T\) 应该移动的方向 \(D_m\) 的 a 或 c。将 \(S_l\) (0 或 1) 放在 a 或 c 的位置,并根据 \(D_m\) 是 a 还是 c 向左或向右移动一个方格。读取新磁带位置的符号,记住它,并将其放在 h 的位置。向右移动直到找到 s。将 s 替换为记住的符号,使用 a 表示 0,c 表示 1。转到步骤 1。
move left until finding a or c, representing the direction
that T should move
q23 symbol to write is 0, direction a = L, c = R
q24 symbol to write is 1, direction a = L, c = R
q25 read new symbol, and replace with h
q26 new symbol = 0, find s on the right, replace with 0,
and fetch next instruction
q27 new symbol = 1, find s on the right, replace with 1,
and fetch next instruction
q28 final state


这就是实现 LCCP UTM 所需的全部内容。不幸的是,读者被剥夺了逐个状态合成 UTM 的乐趣。我记得这曾是我教授自动机理论时最喜欢的任务之一。LCCP UTM 应用于特殊目的 TM 的模拟将在下文说明。
计算两个整数最大公约数的图灵机
为了说明 LCCP UTM 的操作,我将使用一个 TM 来计算两个整数的最大公约数 (GCD)。该函数可以通过欧几里得算法实现,如下所示
int GCD( int m, int n )
{
if ( n < m ) return GCD( n, m );
else
{
int r = n % m;
if ( r == 0 ) return m;
else
{
return GCD( r, m );
}
}
}// GCD
这个原始递归函数可以通过 TM 实现。函数的两个整数参数可以编码为一元格式(例如,3 将编码为 111)并由 0 分隔。以下是 TM 模拟器为计算 6 和 4 的 GCD 所产生的输出。显然结果是 2(以一元格式编码为 11)。GCD TM 的输入和结果以粗体显示。
input file? gcdTM6x4_in.txt
number of simulation steps [0 = indefinite]? 0
; gcdTM6x4_in.txt
;
; TM to compute the primitive recursive function GCD
; (Greatest Common Divisor) by Euclid's algorithm.
;
; gcd( m, n )
; =
; ( <( n, m ) --> gcd( n, m ),
; ==( \( n, m ), 0 ) --> m,
; T --> gcd( \( n, m ), m ) )
;
; Input format: a pair of unary numbers separated by a 0,
; with PLENTY of 0's to the left of the first number.
;
q0 0(q0 0 R) 1(q1 1 L)
q1 0(q2 1 R) 1(q1 1 L)
q2 0(q10 0 R) 1(q3 0 R)
q3 0(q4 0 R) 1(q3 1 R)
q4 0(q4 0 R) 1(q5 0 R)
q5 0(q7 0 L) 1(q6 1 L)
q6 0(q6 0 L) 1(q1 1 L)
q7 0(q7 0 L) 1(q8 1 L)
q8 0(q9 0 L) 1(q8 1 L)
q9 0(q2 0 R) 1(q1 1 L)
q10 0(q11 0 R) 1(q10 1 R)
q11
*
Turing machine: gcdTM6x4_in.txt
12 states;
alphabet: '01', 2 symbols
transition/action matrix:
0 1
q 0 q 0, 0,R q 1, 1,L
q 1 q 2, 1,R q 1, 1,L
q 2 q10, 0,R q 3, 0,R
q 3 q 4, 0,R q 3, 1,R
q 4 q 4, 0,R q 5, 0,R
q 5 q 7, 0,L q 6, 1,L
q 6 q 6, 0,L q 1, 1,L
q 7 q 7, 0,L q 8, 1,L
q 8 q 9, 0,L q 8, 1,L
q 9 q 2, 0,R q 1, 1,L
q10 q11, 0,R q10, 1,R
q11 / /
Simulating turing machine
|q0>000000001111110111100
0|q0>00000001111110111100
00|q0>0000001111110111100
000|q0>000001111110111100
0000|q0>00001111110111100
00000|q0>0001111110111100
000000|q0>001111110111100
0000000|q0>01111110111100
00000000|q0>1111110111100
0000000|q1>01111110111100
00000001|q2>1111110111100
000000010|q3>111110111100
0000000101|q3>11110111100
00000001011|q3>1110111100
000000010111|q3>110111100
0000000101111|q3>10111100
00000001011111|q3>0111100
000000010111110|q4>111100
0000000101111100|q5>11100
000000010111110|q6>011100
00000001011111|q6>0011100
0000000101111|q6>10011100
000000010111|q1>110011100
00000001011|q1>1110011100
0000000101|q1>11110011100
000000010|q1>111110011100
00000001|q1>0111110011100
000000011|q2>111110011100
0000000110|q3>11110011100
00000001101|q3>1110011100
000000011011|q3>110011100
0000000110111|q3>10011100
00000001101111|q3>0011100
000000011011110|q4>011100
0000000110111100|q4>11100
00000001101111000|q5>1100
0000000110111100|q6>01100
000000011011110|q6>001100
00000001101111|q6>0001100
0000000110111|q6>10001100
000000011011|q1>110001100
00000001101|q1>1110001100
0000000110|q1>11110001100
000000011|q1>011110001100
0000000111|q2>11110001100
00000001110|q3>1110001100
000000011101|q3>110001100
0000000111011|q3>10001100
00000001110111|q3>0001100
000000011101110|q4>001100
0000000111011100|q4>01100
00000001110111000|q4>1100
000000011101110000|q5>100
00000001110111000|q6>0100
0000000111011100|q6>00100
000000011101110|q6>000100
00000001110111|q6>0000100
0000000111011|q6>10000100
000000011101|q1>110000100
00000001110|q1>1110000100
0000000111|q1>01110000100
00000001111|q2>1110000100
000000011110|q3>110000100
0000000111101|q3>10000100
00000001111011|q3>0000100
000000011110110|q4>000100
0000000111101100|q4>00100
00000001111011000|q4>0100
000000011110110000|q4>100
0000000111101100000|q5>00
000000011110110000|q7>000
00000001111011000|q7>0000
0000000111101100|q7>00000
000000011110110|q7>000000
00000001111011|q7>0000000
0000000111101|q7>10000000
000000011110|q8>110000000
00000001111|q8>0110000000
0000000111|q9>10110000000
000000011|q1>110110000000
00000001|q1>1110110000000
0000000|q1>11110110000000
000000|q1>011110110000000
0000001|q2>11110110000000
00000010|q3>1110110000000
000000101|q3>110110000000
0000001011|q3>10110000000
00000010111|q3>0110000000
000000101110|q4>110000000
0000001011100|q5>10000000
000000101110|q6>010000000
00000010111|q6>0010000000
0000001011|q6>10010000000
000000101|q1>110010000000
00000010|q1>1110010000000
0000001|q1>01110010000000
00000011|q2>1110010000000
000000110|q3>110010000000
0000001101|q3>10010000000
00000011011|q3>0010000000
000000110110|q4>010000000
0000001101100|q4>10000000
00000011011000|q5>0000000
0000001101100|q7>00000000
000000110110|q7>000000000
00000011011|q7>0000000000
0000001101|q7>10000000000
000000110|q8>110000000000
00000011|q8>0110000000000
0000001|q9>10110000000000
000000|q1>110110000000000
00000|q1>0110110000000000
000001|q2>110110000000000
0000010|q3>10110000000000
00000101|q3>0110000000000
000001010|q4>110000000000
0000010100|q5>10000000000
000001010|q6>010000000000
00000101|q6>0010000000000
0000010|q6>10010000000000
000001|q1>010010000000000
0000011|q2>10010000000000
00000110|q3>0010000000000
000001100|q4>010000000000
0000011000|q4>10000000000
00000110000|q5>0000000000
0000011000|q7>00000000000
000001100|q7>000000000000
00000110|q7>0000000000000
0000011|q7>00000000000000
000001|q7>100000000000000
00000|q8>1100000000000000
0000|q8>01100000000000000
000|q9>001100000000000000
0000|q2>01100000000000000
00000|q10>1100000000000000
000001|q10>100000000000000
0000011|q10>00000000000000
00000110|q11>0000000000000
00000110|q11>0000000000000
Input accepted
138 simulation steps
Elapsed time: 0 seconds
TM description for LCCP UTM:
y00000x00000000001x00001000110x00010001011x00011000110x00100101001x00101001101x00110010001x00111001111x01000010001x01001010101x01010011100x01011011010x01100011000x01101000110x01110011100x01111100010x10000100100x10001100010x10010001001x10011000110x10100101101x10101101011y0
现在重要的是 GCD TM 的描述(上面刚显示过),以便 LCCP UTM 进行模拟。
LCCP UTM 描述
LCCP UTM 的描述及其输入磁带对于 TM 模拟器来说,可以根据上面给出的 LCCP UTM 实现的转移表来编写。输入磁带包含伪磁带和要模拟的 TM 的描述。要模拟的 TM 的伪磁带以粗体显示。
;
; LCCP_UTM_in.txt
;
; Description of the LCCP UTM for simulation
;
29
x01acyhs
;
; Locate Phase
;
q0 x(q1 x L) 0(q0 0 R) 1(q0 1 R) y(q0 y R) h(q0 h R)
q1 x(q1 x L) 0(q1 a L) 1(q1 c L) y(q2 y R)
q2 x(q10 x R) a(q3 0 R) c(q4 1 R)
q3 x(q5 x R) a(q3 a R) c(q3 c R) y(q28 y -)
q4 x(q6 x R) a(q4 a R) c(q4 c R) y(q28 y -)
q5 x(q5 x R) 0(q7 a L) 1(q8 c R) a(q5 a R) c(q5 c R)
q6 x(q6 x R) 0(q8 a R) 1(q7 c L) a(q6 a R) c(q6 c R)
q7 x(q7 x L) 0(q2 0 R) 1(q2 1 R) a(q7 a L) c(q7 c L)
q8 x(q9 x L) 0(q8 a R) 1(q8 c R)
q9 x(q9 x L) 0(q9 a L) 1(q9 c L) a(q9 a L) c(q9 c L) y(q2 y R)
;
; Copy Phase
;
q10 x(q10 x R) 0(q11 a L) 1(q12 c L) a(q10 a R) c(q10 c R)
q11 x(q11 x L) 0(q11 0 L) 1(q11 1 L) a(q11 a L) c(q11 c L) y(q13 y R)
q12 x(q12 x L) 0(q12 0 L) 1(q12 1 L) a(q12 a L) c(q12 c L) y(q14 y R)
q13 x(q16 x L) 0(q15 a R) 1(q15 a R) a(q13 a R) c(q13 c R)
q14 x(q17 x L) 0(q15 c R) 1(q15 c R) a(q14 a R) c(q14 c R)
q15 x(q10 x R) 0(q15 0 R) 1(q15 1 R)
;
; Clean-Up Phase
;
q16 0(q16 0 L) 1(q16 1 L) a(q16 a L) c(q16 c L) y(q16 y L) h(q18 a R)
q17 0(q17 0 L) 1(q17 1 L) a(q17 a L) c(q17 c L) y(q17 y L) h(q18 c R)
q18 x(q19 x R) 0(q18 0 R) 1(q18 1 R) a(q18 0 R) c(q18 1 R) y(q18 y R)
q19 x(q19 x R) 0(q20 0 L) 1(q20 1 L) a(q19 0 R) c(q19 1 R) y(q20 y L)
q20 x(q20 x L) 0(q20 0 L) 1(q20 1 L) y(q21 y R)
q21 x(q22 x L) 0(q21 0 R) 1(q21 1 R)
q22 0(q23 s L) 1(q24 s L)
;
; Perform Phase
;
q23 0(q23 0 L) 1(q23 1 L) a(q25 0 L) c(q25 0 R) y(q23 y L)
q24 0(q24 0 L) 1(q24 1 L) a(q25 1 L) c(q25 1 R) y(q24 y L)
q25 0(q26 h R) 1(q27 h R)
q26 0(q26 0 R) 1(q26 1 R) y(q26 y R) s(q1 0 R)
q27 0(q27 0 R) 1(q27 1 R) y(q27 y R) s(q1 1 R)
q28
*
h00000001111110111100y00000x00000000001x00001000110x00010001011x00011000110x00100101001x00101001101x00110010001x00111001111x01000010001x01001010101x01010011100x01011011010x01100011000x01101000110x01110011100x01111100010x10000100100x10001100010x10010001001x10011000110x10100101101x10101101011y0
!
下图显示了模拟结束时的控制台屏幕。

LCCP UTM 模拟的 GCD TM 为输入 6 (111111) 和 4 (1111) 产生了结果 110h(h 符号左侧为一元格式的 2)。模拟花费了 840,039 步,耗时 42,630 秒(710.5 分钟,11.84 小时)。请注意,模拟器打印了“输入未接受”。当模拟器运行 LCCP UTM 时,总是会打印此消息。
更重要的是,在模拟结束时,有一个 TM 描述用于 LCCP UTM。但在这个例子中,描述的是 LCCP UTM 本身。这意味着 LCCP 可以模拟它自身模拟一个特定的 TM!我在 2003 年就这么做了,模拟花费了近 150 万步。将输出重定向到文件,输出文件大小为 438,874,709 字节。
运行代码
ZIP 文件包含两个目录:Turing 和 tms。Turing 目录包含源文件 Turing.cpp,tms 目录包含本文中描述的所有图灵机的文本文件。要运行代码,请创建一个名为 Turing 的非托管 C++ 解决方案。将 Turing.cpp 的默认代码替换为 Turing 目录中的代码。要模拟图灵机,例如 sampleTM,请将 sampleTM.txt 和 sampleTM_in.txt 文件复制到非托管 C++ 的 Debug 目录。切换到该目录。然后,在命令提示符下,发出命令
Turing.exe <sampleTM.txt
