生成随机 Voronoi 图

function Metric(x,y) {return (x*x + y*y)}
// Generating and plotting Voronoi diagram (simple version).
function pVoronoiD() {
  var cvs=document.getElementById("cvsId");
  var ctx=cvs.getContext("2d");
  var n=7, w=640, x=y=d=dm=j=0, w1=w-2;
  // Arrays for 7 predefined sites (located on canvas) and colors
  X=[20,30,60,80,100,120,140];
  Y=[200,100,300,400,200,400,340];
  C=["red","orange","yellow","green","blue","navy","violet"];
  ctx.fillStyle="white"; ctx.fillRect(0,0,w,w);
  // Plotting sites and applying linked color.
  for(y=0; y<w1; y++) {
    for(x=0; x<w1; x++) {
      dm=w1*w1 + w1*w1; j=-1;
      for(var i=0; i<n; i++) {
        d=Metric(X[i]-x,Y[i]-y)
        if(d<dm) {dm=d; j=i;}
      }//fend i
      ctx.fillStyle=C[j]; ctx.fillRect(x,y,1,1);
    }//fend x
  }//fend y
  // Plotting site points (in black). Note: these 7 lines were added later! LOL
  // Also, there was no title, h3 and comment tags. No JS comments too. Only 21 lines.
  // I've re-formatted it later to look like now (and match prime page code).
  ctx.fillStyle="black";
  for(var i=0; i<n; i++) {
    ctx.fillRect(X[i],Y[i],3,3);
  }
}

// Helper Functions
// HF#1 Like in PARI/GP: return random number 0..max-1
function randgp(max) {return Math.floor(Math.random()*max)}
// HF#2 Random hex color returned as "#RRGGBB"
function randhclr() {
  return "#"+
  ("00"+randgp(256).toString(16)).slice(-2)+
  ("00"+randgp(256).toString(16)).slice(-2)+
  ("00"+randgp(256).toString(16)).slice(-2)
}
// HF#3 Return the value of a metric: Euclidean, Manhattan or Minkovski
function Metric(x,y,mt) {
  if(mt==1) {return Math.sqrt(x*x + y*y)}
  if(mt==2) {return Math.abs(x) + Math.abs(y)}
  if(mt==3) {return(Math.pow(Math.pow(Math.abs(x),3) + Math.pow(Math.abs(y),3),0.33333))}
}
// Generating and plotting Voronoi diagram.
function pVoronoiD() {
  var cvs=document.getElementById("cvsId");
  var ctx=cvs.getContext("2d");
  var w=cvs.width, h=cvs.height;
  var x=y=d=dm=j=0, w1=w-2, h1=h-2;
  var n=document.getElementById("sites").value;
  var mt=document.getElementById("mt").value;
  // Building 3 arrays for requested n random sites (located on canvas)
  // and linked to them random colors.
  var X=new Array(n), Y=new Array(n), C=new Array(n);
  ctx.fillStyle="white"; ctx.fillRect(0,0,w,h);
  for(var i=0; i<n; i++) {
    X[i]=randgp(w1); Y[i]=randgp(h1); C[i]=randhclr();
  }
  // Plotting sites and applying selected mt metric and linked colors.
  for(y=0; y<h1; y++) {
    for(x=0; x<w1; x++) {
      dm=Metric(h1,w1,mt); j=-1;
      for(var i=0; i<n; i++) {
        d=Metric(X[i]-x,Y[i]-y,mt)
        if(d<dm) {dm=d; j=i;}
      }//fend i
      ctx.fillStyle=C[j]; ctx.fillRect(x,y,1,1);
    }//fend x
  }//fend y
  // Plotting site points (in black).
  ctx.fillStyle="black";
  for(var i=0; i<n; i++) {
    ctx.fillRect(X[i],Y[i],3,3);
  }
}

## VORDgenerator.R

## Voronoi Diagram Generator

#  Helper Functions
## HF#1 Random hex color returned as "#RRGGBB".
randHclr <- function() {
  m=255;r=g=b=0;
  r <- sample(0:m, 1, replace=TRUE);
  g <- sample(0:m, 1, replace=TRUE);
  b <- sample(0:m, 1, replace=TRUE);
  return(rgb(r,g,b,maxColorValue=m));
}
## HF#2 Return the value of a metric: Euclidean, Manhattan or Minkovski
Metric <- function(x, y, mt) {
  if(mt==1) {return(sqrt(x*x + y*y))}
  if(mt==2) {return(abs(x) + abs(y))}
  if(mt==3) {return((abs(x)^3 + abs(y)^3)^0.33333)}
}

## Generating and plotting Voronoi diagram.
## ns - number of sites, fn - file name, ttl - plot title.
## mt - type of metric: 1 - Euclidean, 2 - Manhattan, 3 - Minkovski.
pVoronoiD <- function(ns, fn="", ttl="",mt=1) {
  cat(" *** START VD:", date(), "\n");
  if(mt<1||mt>3) {mt=1}; mts=""; if(mt>1) {mts=paste0(", mt - ",mt)};
  m=640; i=j=k=m1=m-2; x=y=d=dm=0;
  if(fn=="") {pf=paste0("VDR", mt, ns, ".png")} else {pf=paste0(fn, ".png")};
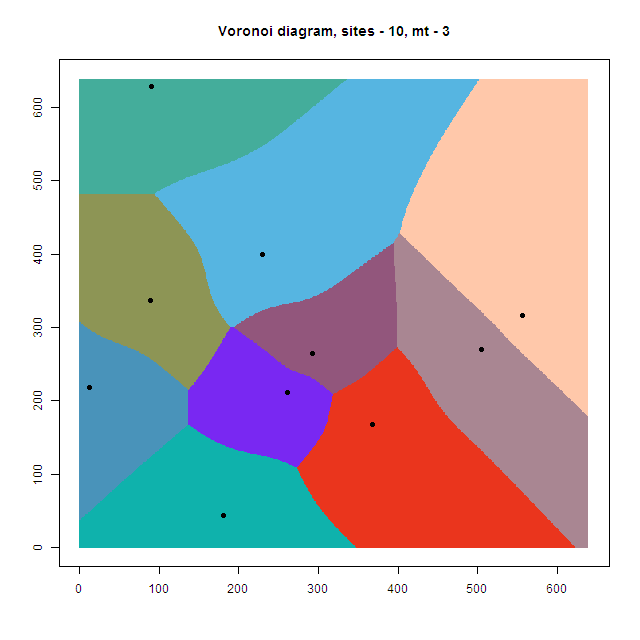
  if(ttl=="") {ttl=paste0("Voronoi diagram, sites - ", ns, mts)};
  cat(" *** Plot file -", pf, "title:", ttl, "\n");
  plot(NA, xlim=c(0,m), ylim=c(0,m), xlab="", ylab="", main=ttl);
  # Building 3 arrays for requested n random sites (located on canvas)
  # and linked to them random colors.
  X=numeric(ns); Y=numeric(ns); C=numeric(ns);
  for(i in 1:ns) {
    X[i]=sample(0:m1, 1, replace=TRUE);
    Y[i]=sample(0:m1, 1, replace=TRUE);
    C[i]=randHclr();
  }
  # Plotting sites and applying selected mt metric and linked colors.
  for(i in 0:m1) {
    for(j in 0:m1) {
      dm=Metric(m1,m1,mt); k=-1;
      for(n in 1:ns) {
        d=Metric(X[n]-j,Y[n]-i, mt);
        if(d<dm) {dm=d; k=n;}
      }
      clr=C[k]; segments(j, i, j, i, col=clr);
    }
  }
  # Plotting site points (in black).
  points(X, Y, pch = 19, col = "black", bg = "white")
  dev.copy(png, filename=pf, width=m, height=m);
  dev.off(); graphics.off();
  cat(" *** END VD:",date(),"\n");
}
## Executing:
#pVoronoiD(10)           ## Euclidean metric
#pVoronoiD(10,"","",2)   ## Manhattan metric
#pVoronoiD(10,"","",3)   ## Minkovski metric
#pVoronoiD(150)          ## Euclidean metric

正如您所见，R 中的所有函数都具有与 JavaScript 相同的函数功能和相同的步骤，因为它们被适应了 R 的本地运算符和函数。就是这样！

您可以在下图本身中查看 4 个用 R 绘制的 Voronoi 图。

结论

提供了两个 Voronoi 图生成器：HTML/JavaScript 页面和 R 脚本，这就是这个项目的全部源代码。

应该强调的是，开头引用的 [1] 中的 VD 定义只是众多可能性之一，特别是如果 VD 用于显示温度、水或更抽象的东西。度量也可能与任何距离无关，而是充当“爱情计”或“情绪计”，例如。

无论如何，在许多研究中，随机选择的站点和颜色应该是预定义的，而不是随机的。甚至“点”的顺序也可以改变以适应绘图算法。要确定如何重新排列站点以进行适当的绘图，请观看绘图过程的动画。如果您的计算机不是超快的，您可以在“RGui”窗口的“R Graphics”子窗口中观看“动画”。

这意味着脚本需要修改。幸运的是，这些脚本很小且清晰，因此修改它们并不难。

注意：“现实世界”或理论应用不在本文讨论范围内。

所呈现的算法肯定可靠，因为它们已经支持 7 种语言 [5]。另一个合理的问题是：“它适合您的应用任务吗？”

要找到答案：用您的语言实现它并进行测试！别无他法。

最后，使用“VD 生成器”作为模板，任何人都可以开始任何适合将结果显示为彩色 Voronoi 图的研究。

参考文献

1. Voronoi 图，维基百科，免费百科全书，网址：https://en.wikipedia.org/wiki/Voronoi_diagram。
2. Drysdale D. Voronoi Diagrams: Applications from Archaology to Zoology. (1993), Regional Geometry Institute, Smith College. 网址：http://www.ics.uci.edu/~eppstein/gina/scot.drysdale.html。
3. Snow, J. On the Mode of Communication of Cholera. (1855), London: John Churchill. 网址：http://www.ph.ucla.edu/epi/snow/snowbook.html。
4. Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques.. (1907), J. reine angew. Math. 133, 97-178。
5. Voronoi 图，Rosetta Code Wiki，网址：http://rosettacode.org/wiki/Voronoi_diagram。
6. Haugland. K. Create a Voronoi diagram 1 of 2. (2012), Code Project, 网址：https://codeproject.org.cn/Articles/411242/Create-a-Voronoi-diagram-of。
7. Haugland. K. Create a Voronoi diagram 2 of 3. (2012), Code Project, 网址：https://codeproject.org.cn/Articles/413452/Create-a-Voronoi-diagram-of。
8. Joukhadar, B. Fast Voronoi Diagram in C#. (2014), Code Project, 网址：https://codeproject.org.cn/Tips/797123/Fast-Voronoi-Diagram-in-Csharp。
9. Stadnik, V. Simple approach to Voronoi diagrams. (2015), Code Project, 网址：https://codeproject.org.cn/Articles/882739/Simple-approach-to-Voronoi-diagrams。
10. BenDi. Fortune's Voronoi algorithm implemented in C#. (2015), Code Project, 网址：https://codeproject.org.cn/Articles/11275/Fortune-s-Voronoi-algorithm-implemented-in-C。
11. Voevudko, A.E. Generating Kronecker Product Based Fractals. (2017), Code Project, 网址：https://codeproject.org.cn/Articles/1189288/Generating-Kronecker-Product-Based-Fractals。