生成基于克罗内克积的分形

• 下载完整项目源代码 - 12 Kb

引言

分形[1-6]是惊人的，通常色彩鲜艳的图像，它们已经被创造和欣赏了几个世纪，但直到上个世纪末才开始对其进行研究和计算机生成。

这是一个简单的定义

在我们的例子中，分形看起来像几何图形，它们通常被称为绘图或图形。

分形有很多类型/类别，例如：基于IFS[7]、L-系统生成[8]、使用混沌游戏方法[9]创建等。在[6]中欣赏巨大分形图库，并熟悉其中的一些。实际上，[7]和[8]都是非常好的在线分形生成器。它们甚至允许用户输入自己的对象：[7]中的表格，以及[8]中的公理、生产规则和其他参数集。

本项目为任何网站所有者提供使用项目组件集作为几乎无限数量（好吧，几乎是……）分形在线生成器。此外，任何用户都可以将此项目软件用作桌面应用程序。只需下载并开始使用。

仅需4个HTML页面和1个JavaScript文件即可呈现您需要成为特殊分形设计师的非常紧凑的源代码。每个人都已拥有一台可靠的工具来生成分形：那就是浏览器，它唯一的要求是支持“canvas”对象。

关于基于Kronecker积的分形

本文仅描述基于Kronecker积[10]的分形（KPBF）及其与我们的“KPBF生成器”相关的特性。

应该强调的是，在许多书籍和文章[11-20]中都提到了使用Kronecker积制作分形，并展示了一些分形的图片。其中一些展示了一些初始矩阵的样本，但没有一个清楚地描述了使用Kronecker积所需的程序。

让我们从一个定义开始

备注

• 换句话说，这仅仅意味着这样的矩阵可以用来生成分形图像。
• 所有定义都将主要应用于与Kronecker积相关的分形。

以下陈述/引理可以轻松检查，甚至可以正式证明

分形图像的本质是自复制（至少是自相似复制）。在我们这里产生这种自相似复制的方法非常简单。创建分形矩阵的正式递归算法如下。

让我们仔细看看VOE.js - 一个小的JavaScript库，只包含真正通用的绘图辅助函数，这些函数已经被使用了很多次并证明了它们的有用性和可靠性[21]。

这里将简要描述两个关键函数：mkp2()和pmat01()。

第一个函数是mkp2()，它实现了Kronecker积。

  // HFJS#5: Return the Kronecker product of the a and b matrices.
  // Note: both a and b must be matrices, i.e., 2D rectangular arrays.
  function mkp2(a,b) {
    var m=a.length, n=a[0].length, p=b.length, q=b[0].length;
    var rtn=m*p, ctn=n*q; var r=new Array(rtn);
    // Building final matrix filled with zeros.
    for (var i=0; i<rtn; i++) {r[i]=new Array(ctn)
      for (var j=0;j<ctn; j++) {r[i][j]=0} }
    // Calculating final KP matrix.
    for (var i=0; i<m; i++) {
      for (var j=0; j<n; j++) {
        for (var k=0; k<p; k++) {
          for (var l=0; l<q; l++) {
            r[p*i+k][q*j+l]=a[i][j]*b[k][l];
          }}}}//all4forend
    return(r);
  }

您可以看到，它包含简单的2个步骤

• 构建填充零的最终矩阵。
• 使用嵌套的4个循环遍历2个矩阵的4个维度来计算最终KP矩阵。

哦，历史上第一个这样的函数是mkp() - 用于相同产品的箭头函数[21]。这里使用了mkp2()，因为如果您愿意，可以更容易地将其“翻译”成您的语言。顺便说一句，在[21]中查找是否有适合您语言的，有20多种语言样本。

即使仅仅查看最终矩阵，您也可以看到要绘制的分形。换句话说：从二阶分形矩阵开始，就已经很适合绘制了。

要理解绘图技术，请仔细查看pmat01().

  // HFJS#3: Plot any matrix mat (filled with 0 & not 0 items).
  //         Set error p in the page: <p id="epId"></p>, sc - Scale (0..max)
  //         fgc/bgc - FG/BG colors; rt - rotate 90 degree if true (once).
  function pmat01(mat, fgc, bgc, sc, rt) {
    // Setting basic vars for canvas and matrix
    var cvs = document.getElementById('cvsId');
    var ctx = cvs.getContext("2d");
    var w = cvs.width, h = cvs.height;
    var m = mat[0].length, n = mat.length, k=0, dsz=1;
    console.log("MAT rxc", n, "x", m); // n - rows. m - cols
    if(n<21&&m<21) {matl2cons("MAT2PLOT",mat)}
    if(sc!=1) {ctx.scale(sc,sc)};
    if(sc<0.9) {dsz=2};
    // Setting BG and plotting FG colors
    ctx.fillStyle=bgc; ctx.fillRect(0,0,w,h);
    ctx.fillStyle=fgc;
    // Plotting "dots" (!=0 values in matrix) & counting them.
    // n - rows. m - cols
    for(var i=0; i<n; i++) {
      for(var j=0; j<m; j++) {
        if(mat[i][j]!=0) { k++;
          if(rt&&n==m) {ctx.fillRect(i,j,1,1)} else {ctx.fillRect(j,i,1,1)}
        };
      }//fend j
    }//fend i
    // Outputting fractal matrix "signature": matrix sizes & number of dots.
    var ms="Matrix("+n+"x"+m+") "+k+" dots";
    var ep=document.getElementById("epId").innerHTML;
    document.getElementById("epId").innerHTML=ep+"<br>"+ms;
  }//func end

正如您所见，它是一个非常小、简单的函数，它将绘制任何合法矩形JavaScript矩阵的分形矩阵。这个函数非常清晰，没什么复杂的：它将矩阵解释为具有x、y坐标的画布点/点，并在矩阵中的值不等于零时打印一个点。

在我们的KPBF的情况下，我们已经有了矩阵，并且不难找出如何绘制它。

几年前，我曾感到困惑：为什么在PARI/GP或R脚本中没有一张布朗树的图片？

所以我从PARI/GP开始

• 创建矩阵来收集随机“移动”，并最初填充零。稍后在矩阵的访问单元格中放入1。
• 创建了与此处使用的类似的分片辅助函数。
• 结果，生成并绘制了4种类型的布朗树[22]。

后来我在R中重复了所有这些步骤。现在有很多布朗树，包括在PARI/GP和R[22]中制作的。

现在，任何用户都有一个清晰的创建KPBF的算法和用于绘制分形的绘图辅助函数。此外，这个辅助函数还可以用于绘制任何其他类型的基于点的分形，例如上面提到的布朗树。

这类分形几乎有无限多种。您仅受限于您的创造力和计算机的强大功能。

非正式的虚拟无穷定义简短而简单：不同大小和不同内容的矩阵将产生不同的分形。让我们为无穷定义添加颜色：不同的颜色 - 不同的分形。当然，这有点推测，但仍然有助于我们的理解。

通常用户从二阶开始，因为一阶意味着初始矩阵本身（还没有Kronecker积）。

下一阶复制可以放大或缩小，或者只是在一个或多个方向上扩展到无穷大。在大多数情况下，用户可以计算其分形的阶数，从最小的基本子图形（例如，“加号”分形中的微小“+”）到最大的绘制图形。这在下面的图片中显示了该分形的阶数1、2和3。

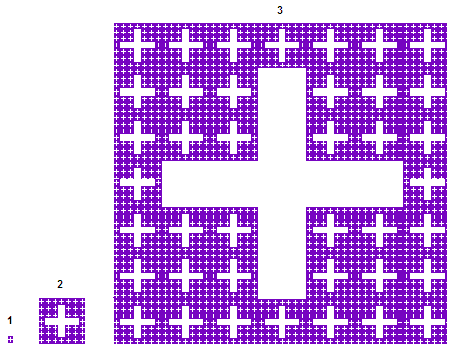
注意：最小和最大的子图形可能不可见或仅部分可见。

一些作者称一种与众不同的特殊分形为“变种”。我更喜欢称它们为“同胞”，因为在大多数情况下，它们实际上是一种新型的“地毯”分形。这些“同胞”具有：多个子图像的不同配置，每阶和层级的数量不同。我更喜欢称它们为“地毯”，而不是“地毯”。它们对我来说看起来确实像小区域地毯。

自己看看下面的图。

我同意称下一个为“谢尔宾斯基地毯变种”，因为它（总体上）复制了谢尔宾斯基地毯[3]的结构，但中心正方形错位了。

令人惊讶的是，这是我在[17]中找到的唯一一个“变种”。这里展示的其他所有都是我的“同胞”。此外，在“演示”页面中可以找到一些其他。

下图显示了谢尔宾斯基三角形分形和三个三角形同胞分形。

正如您所看到的，它们确实是新的三角形分形。与谢尔宾斯基三角形[4]的唯一共同点是三角形的基本图像。在“演示”页面中可以找到一些额外的三角形同胞分形。

备注

• Kronecker积很顽固，有时它拒绝从任何矩阵生成分形，尤其是从矩形矩阵（即非方形矩阵）生成。
• 此外，基本矩阵/图像可能会不可预测地旋转。
• 请记住：漂亮多彩的分形背景来自数字1，零给出分形的基本图形（白色）。但这取决于分形创建者的观点，即“基本图像是什么？”。

使用页面

使用“演示”页面

从“KPBF生成器”的“演示”页面开始，该页面具有教育目的。您可以尝试不同阶数和颜色的各种流行分形和许多新分形。在“演示”页面的下拉列表中，前4个分形是众所周知的，但其他分形是在去年使用R脚本“发现”的。众所周知的分形如下：谢尔宾斯基地毯和三角形[3,4,11,13,15,16]（上面已显示），Vicsek[2,20]，At LaGuardia[18,20]，棋盘格[15,16]和六边形[18]。它们在下面的图中显示。前三个也可以在维基百科上找到，但使用了不同的方法。

新分形也很漂亮，前所未见，或者至少很难找到：棋盘格，“H”，地毯，“5/2”和许多附加分形。

使用“设计”页面

“设计/绘图”双页面是“KPBF生成器”的一部分。它允许任何用户通过“设计”页面直观地设计和构建分形矩阵，然后将其发送到选定的绘图页面，并尝试该矩阵可用的所有阶数。

“设计”页面是独一无二的，但常规的“绘图”页面几乎是“演示”页面的副本。它使用用户熟悉的下拉菜单和消息等。

您可以在下图中看到这两个页面（部分显示）。

“设计”页面会告诉用户他创建的矩阵是好是坏。如果仍然很差，那么用户需要根据错误消息或任何其他线索来纠正该矩阵代码。无论如何，“绘图”按钮在这种情况下都会被阻止。

请注意显示的矩阵“签名”，它显示矩阵尺寸和生成的点数。上面图中的签名是：Matrix(243x243) 3125 dots。（对于Vicsek分形，阶数5）。

应该提到的是，所有页面都会对创建的矩阵进行密集检查，以防止浏览器崩溃，即检查所有可以轻松检查的内容。这有点复杂，因为标准的JavaScript中没有矩阵对象。总之，编写/测试类似编译器的脚本是不值得的。如果出现错误，- 没有损失，只需点击一下即可返回或重新加载页面。事实上，用户仍然可以从浏览器调试器（Chrome中）收到额外的错误通知。在这种情况下，- 只需保存矩阵代码并重新加载“设计”页面。

注意：创建的矩阵可以在控制台日志（Chrome中）中以自然的矩形形式查看。建议在测试新矩阵代码时保持控制台打开。

在此添加如此彻底的矩阵控制之前，如果任何页面达到内存限制，- 我的Chrome浏览器就会崩溃并告诉我：“Aw, Snap! Something went wrong while displaying this webpage. Kill or Reload page。”现在，这种情况已经不再发生。

建议新用户将JavaScript矩阵代码精确地插入“设计”页面的大文本区域中，如上图所示。因为它有助于用户直观地控制列数和矩阵的代码语法。无论如何，在脚本删除所有空格后，矩阵代码将转换为一行代码。

在“演示”页面的脚本中，查找使用的矩阵的代码（大多写在一行中，如下所示）。

  // Well known fractals
  if(fi==1) M=[[1,1,1],[1,0,1],[1,1,1]];
  if(fi==2) M=[[1,1],[0,1]];
  if(fi==3) M=[[0,1,0],[1,1,1],[0,1,0]];
  if(fi==4) M=[[1,1,1,1],[1,1,0,0],[1,0,1,0],[1,0,0,1]];
  // New fractals
  if(fi==5) M=[[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[0,0,0,0,1,1,1,1],[0,0,0,0,1,1,1,1],[0,0,0,0,1,1,1,1],[0,0,0,0,1,1,1,1]];
  if(fi==6) M=[[1,1,1,1,1,1,1],[1,0,0,0,0,0,1],[1,1,1,0,1,1,1],[1,1,1,0,1,1,1],[1,1,1,0,1,1,1],[1,0,0,0,0,0,1],[1,1,1,1,1,1,1]];
  ...

使用“绘图”页面

有两个绘图页面：用于常规测试绘图和用于精细发布质量绘图。如果是测试 - 请使用“常规绘图”页面。它工作速度更快。

如果准备Code Project的文章 - 请使用“精细绘图”页面（部分显示如下）。

“精细绘图”页面允许用户

• 输入前景颜色（FG）和/或背景颜色（BG）。这将覆盖选定的颜色（如果有）和默认的白色背景。
• 设置比例，以帮助图像很好地适应画布框架。
• 设置画布的方形大小（越大越好）。
• 将图像旋转一次，90°。

• 如果您将矩阵大小设置为600，并且画布区域中没有任何图像，请查看签名。如果显示：“Matrix(2187x2187) 78125 dots”，则生成的图像将太大。实际上，几乎是原来的4倍（2187/600）。在这种情况下，- 先将比例设置为0.25，然后再次绘制。
• 如果比例小于1，颜色将褪色。因此，选择阶数以尽可能接近画布大小。例如，在Vicsek分形的情况下：最好使用阶数6，而不是5。
• 单击“返回设计”链接将重置“设计”页面，这对于新矩阵来说是很好的。如果您需要更新设计的矩阵，请使用浏览器的“后退”按钮。

结论

“KPBF生成器”由4个HTML页面和1个JavaScript文件组成，这是该项目的全部源代码。

此外，还有一个包含精选测试矩阵代码列表的奖励文件。此列表将帮助用户理解此类分形生成的工作原理以及从任何矩阵中可以期待什么。

以下是与此类分形相关的一些新（或至少是难以找到）特性的*摘要*

• 并非每个分形矩阵（即使是仅包含0/1的矩阵）都会生成分形图像。
• 如果交换0和1，则可以产生所谓的“反转”分形。但这取决于哪一个分形被称为“正向”，哪一个被称为“反向”。
• 只需要1个零，但可以使用任何整数代替数字1。
• 除了众所周知的分形之外，还可以轻松生成它们的“同胞”，它们也很漂亮。
• 使用不同的语言/工具（例如R、PARI/GP等），可以从同一个分形矩阵生成外观不同的分形。这是因为一些绘图工具会自动应用不同类型的缩放，而且这通常是不可控的。

对于没有内置Kronecher积函数（或运算符）的语言，Rosetta Code Wiki[21]上已经构建并展示了许多自定义函数。在那里还可以找到一些新的分形[23]。

这是一个有趣的问题，仍然是一个开放的问题：为什么使用不同的方法，例如IFS基础、L-系统生成等，或者即使只使用递归函数，- 仍然可以重现谢尔宾斯基地毯或三角形[3,4]？

理论和实践应用可以在[12,17,18]中找到。几乎所有应用领域都在《分形杂志》[19]中涵盖。

最后，“KPBF生成器”使任何人，即使没有编程背景，都可以成为这一相当广泛（几乎无限）类别分形的设计师、发明家和创造者。

参考文献

1. 分形，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/Fractal。
2. Vicsek分形，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/Vicsek_fractal。
3. 谢尔宾斯基地毯，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/Sierpinski_carpet。
4. 谢尔宾斯基三角形，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/Sierpinski_triangle。
5. 分形类别，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/Category:Fractals。
6. 按豪斯多夫维数分列的分形列表，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/List_of_fractals_by_Hausdorff_dimension。
7. Toal R.，迭代函数系统，网址：http://cs.lmu.edu/~ray/notes/ifs/。
8. Roast K.，L-Systems Turtle Graphics Renderer，网址：http://www.kevs3d.co.uk/dev/lsystems/。
9. 混沌游戏，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/Chaos_game。
10. Kronecker积，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/Kronecker_product。
11. Gazalé, Midhat J. (1999)，Gnomon: From Pharaohs to Fractals，普林斯顿大学出版社，ISBN 9780691005140。
12. Xue D., Zhu Ya., Zhu G.-X. and Yan X. Generalized kronecker product and fractals, Proc. SPIE 2644, Fourth International Conference on Computer-Aided Design and Computer Graphics, 75, (1996), doi:10.1117/12.235499。
13. Haugland K，分形理论与实践，(2013)，网址：https://codeproject.org.cn/Articles/650821/Fractals-in-theory-and-practice。
14. Steeb W.-H. (1997)，Matrix Calculus and Kronecker Product with Applications and C++ Programs., World Scientific Publishing，ISBN 9810232411
15. Hardy A., Steeb W.-H. (2008)，Mathematical Tools in Computer Graphics with C# Implementations，World Scientific，ISBN 9789812791023。
16. Steeb W.-H. (2014)，The Nonlinear Workbook. Chaos, Fractals, Cellular Automata, Genetic Algorithms, Gene Expression Programming, Support Vector Machine, Wavelets, Hidden ... Java and SymbolicC++ Programs, (第6版)，World Scientific Publishing Company，ISBN: 9789814583473。
17. Stepanyan I.V., Petoukhov S.V. The Matrix Method of Representation, Analysis and Classification of Long Genetic Sequences. (2013)。网址：https://arxiv.org/abs/1310.8469v1。
18. Leskovec J., Chakrabarti D., Kleinberg J. 等人。Kronecker Graphs: An Approach to Modeling Networks. (2010)，Journal of Machine Learning Research 11，网址：https://cs.stanford.edu/people/jure/pubs/kronecker-jmlr10.pdf。
19. 分形杂志，World Scientific，网址：http://www.worldscientific.com/page/fractals/aims-scope。
20. Wicklin R., Self-similar structures from Kronecker products, (2014)，网址：http://blogs.sas.com/content/iml/2014/12/17/self-similar-structures-from-kronecker-products.html。
21. Kronecker积，Rosetta Code Wiki，网址：http://rosettacode.org/wiki/Kronecker_product。
22. 布朗树，Rosetta Code Wiki，网址：http://rosettacode.org/wiki/Brownian_tree
23. 基于Kronecker积的分形，Rosetta Code Wiki，网址：http://rosettacode.org/wiki/Kronecker_product_based_fractals。。

历史

2017年5月27日 文章初次发布。

2017年5月30日 清理提交向导剥离的标签等遗留内容。添加“历史”。