使用等距计算机键盘进行音乐学习

• 下载源代码 — 39.5 KB

题记

沙发左边是一架老式英国三角钢琴。钢琴前坐着我亲爱的黑发姐姐柳博奇卡；她用刚用冷水洗过的粉嫩手指，明显很费力地弹奏着克莱门蒂的练习曲。她十一岁了……只能用琶音的方式弹奏八度。

列夫·尼古拉耶维奇·托尔斯泰，《童年》，第二章. 妈妈

— 我有权利……吗？
— 哦，是的，你有！
— 那么，我可以……吗？
— 不，你不能。

一则关于人权的旧笑话

目录

洞见
动机
音系的数学观点
必要的音符
有理数与无理数
轨道
音系是格，而非序列
毛细胞共振
文化与物理
更好的记谱法
编程
同构MIDI键盘应用程序
特点
MIDI API
键盘尺寸
构建
使用键盘
指法图
调式
“音乐变形五角星”
混合利底亚调式的奥秘
和弦
和弦结构
键盘的反击：按键冲突问题
和弦结构并非唯一
和弦名称
和弦预设
未来工作
未来已来
结论

这是专门讨论使用基于计算机键盘的特制键盘进行音乐学习系列文章的第二篇。

1. 本文
2. 使用半音格键盘进行微音音乐学习
3. 声音构建器，Web Audio 合成器
4. 多点触控支持，用于十指弹奏

洞见

让我们从简单的事情开始。比如说，我们想在电脑上玩一些声音。

显然，第一个想法是使用现成的电脑键盘。我们能用它做什么呢？我们可以模仿钢琴键盘，很多应用程序都这么做，但这有什么意义呢？键盘的键行很短，最多也就12-13个键。钢琴键盘又有什么用呢？不，如果我们想试验声音、学习和声，只有使用某种半音体系才有意义。

毕竟，计算机键盘与线性结构的钢琴键盘完全不同。它更像是一个由四个较短的键行组成的矩阵，其中第一行和最后一行不太适合这个目的，所以我们最好将自己限制在四行之内。值得注意的是，每一行中的按键相对于上一行或下一行都水平偏移了大约半个键宽。也就是说，这种几何形状非常接近平移对称。这不正是我们想要的吗？我们可以将这组按键视为一个秩为2的点的格，并将一组音高与之关联。要做出决定，我们只需要考虑相邻两行中的三个相邻按键——这将定义所有其他按键的音高。这个由3个键组成的子集可以被看作是周期格的基本域。然后我们只需为这个模式选择两个纯音程：一个用于同一行内按键之间的音程，另一个用于行与行之间的音程。

等等……只有两个音程被称为“纯”音程：纯四度和纯五度。难道我们还需要比“纯”更差的东西吗？:-) 那么，既然一行中的音高应该从左到右递增，我们就把左上角的键指定为纯四度，右上角的键指定为纯五度。它们之间的音程是一个全音，所以这应该就是每行任意两个相邻按键之间的音程。搞定。

这样，由于对称性，我们必须将下方的键视为被赋予了某个基频的键，而其他两个键的决定则是自动产生的。在西方共晓时期的音系中，这三个音符可以被看作是传统大调音阶的第1、第4和第5级音。这些级数显示在图片上，“距离”则是有理频率比值和以半音为单位的距离（括号内）。

但我们为什么只考虑纯音程，这两个音程又有什么特别之处呢？全音音程也很特殊——我会称之为“第二基本音程”。为什么？因为这些音程在整个音乐和声中扮演着最基本的角色。尽管我们从“西方”共晓时期的自然音阶体系开始，这种“纯粹性”远远超出了这个范围：它根植于物理学、数学和音乐感知的最基本原理。因此，音高之间的两种特殊频率关系在任何可想象的音乐文化和音系中都是最基本的——它们被以一种特殊的方式感知，因为它们紧随更基本的同度（齐奏）和八度音程之后，在泛音方面是最特殊的。

我将尝试在下面更详细地解释这种基本性质。

动机

这个想法并没有什么新意，除了或许是使用计算机键盘和特定的键盘几何布局这个想法。同构键盘确实存在，其价值也基本得到了解释。

另见：移调等效性。

对我来说，灵感的主要来源是六边形的威基-海登音符布局。

另见：Jammer键盘，它已经以商业硬件的形式实现，以及Thummer键盘。另一种变体是扬科键盘。

尽管几何差异巨大，我还是在一个UI应用程序中实现了“威基-海登”和“扬科”两种布局：我的版本使用普通的矩形按键。然而，结构上的同构更为重要。但问题仍然存在：计算机键盘的形状和布局仅仅是一种被迫的妥协，比六边形的威基-海登键盘差很多吗？我不会这么说：恰恰相反，我认为计算机键盘的形状和布局有其优点，并且可以用于设计真正的乐器。首先，我认为它更容易记忆和导航。

同时，建议的键盘布局强烈暗示了某些深深植根于音乐本质的音调关系。

我认为理解这些根源是一个双重问题。首先，对基本原理的通常解释被笨拙的、充满冗余的、术语极其复杂且充满纯粹历史特殊性的解释所严重混淆，而记谱法以一种非常间接的方式展示了一些真实且往往相当简单的结构。另一方面，一些最重要且不平凡的要点几乎从未被明确阐述。通过计算机化的研究和一些近乎初级的分析，我想提供一些思考的素材，首先是为我自己，一个非专业音乐家，更多地是从对科学的某种理解出发。我也想激发一些批判性和理性的思考。

音系的数学观点

必要的音符

大部分的思考都基于西方共晓时期对音乐和声的看法，特别是现代西方的十二音平均律音系。同时，大多数思考的范围比这更广，因此它们可以应用于许多其他体系。十二音体系主要用于通过非常熟悉的声音以及图形来清晰地说明所有主题。

我假定读者至少熟悉最基本的音乐概念，特别是音高、音程、音频、音阶和和弦的概念，以及现代西方记谱法的基础，首先是拉丁字母记谱法（C-D-E… 音符带有升/降/还原记号：♯、♭ 和 ♮）。对这些音符的声音有一个相当好的了解也是有益的，但如果这是一个问题，可以很容易地学会，例如……使用本文页面上以源代码形式提供的应用程序——这个应用程序的主要目的是作为一个学习和演示的设备。

即使读者不具备这些先决条件，通过适当的阅读学习这些内容也不是太难。我还通过文章中的链接建议了一些有用的读物。阅读和理解中等复杂度的数学文本的技能会很有用，但并非绝对必要。

有理数与无理数

当我用3/2、4/3 和 9/8的频率比来描述和声音程时，我耍了个小聪明。实际的音程取决于律制，并且通常与这些精确的和声音程有所不同。我希望许多人能看出来或很好地理解这方面。我只是没找到更好的方法来循序渐进地解释事情。这实际上是整个音乐中一个相当痛苦的问题，主要是因为它很难解释，特别是对音乐家来说，更不用说那些对这个问题要么一无所知，要么因为事实和解释的混乱而面临重大困惑的音乐学生了，这些解释往往掩盖而非揭示事物的本质。

让我们从一些非常基础的东西开始。我们应该如何理解音高？几个音调的频率是以对数尺度感知的。换句话说，如果两个音程的终点音高频率是由起点音高频率乘以相同的因子生成的，那么这两个音程就被感知为相等的。主观上，频率是乘法的。从这个意义上说，任何表示音高值的数字都必须是频率的对数量度。在这种情况下，音高值是加法的。

现在，让我们来看看一个音高的泛音。第一泛音对应于某个振荡器的基频，而第二泛音，即双倍频率，在人类感知中（以及许多其他动物，这已通过实验得知）与基频的关联非常强烈，以至于相差一个或多个八度的音高被认为是“类似的”或“相同的”。这被称为八度等价原则。其他泛音的频率是基频的3倍、4倍，以此类推。哪一个可以作为音高单位呢？没有一个可以。这样的单位不可能是泛音。

由于八度等价性，任何升序/降序的音高系统都可以被认为是循环的，因为当它越过八度边界时，它就变成了原始八度中类似音高的等价音高。这种表示法被称为半音圈。

.

这张图上有一个细节可能令人困惑：第7级音位于降B，而不是B，正如它在大调音阶中应有的位置。我将稍后解释这个选择（以及这仅仅是一个选择的事实）。

首先要注意的是，F和G是唯一对称分布的非变音音符。主音与这两个音符之间的音程是5个和7个半音，但如果从高到低逆时针计算，7也可以被视为5，所以这两者是互补的。让我们看看涉及到哪些泛音。F的频率比是4:3，G的频率比是3:2。除了同度的1:1和八度的2:1之外，这组分子/分母对是最简单的。现在，F和G之间全音的频率比是次简单的，因为F和G的比值组合起来得到9:8。

这些音程听起来总是悦耳且“协和”的，尤其是纯五度，完全不受听者特定文化的影响。这是因为我们的听觉系统的自然工作方式。它也是由一组弦组成的，每根弦不仅对其自身的基频产生共鸣，也对其泛音产生共鸣。对较低泛音的响应更强，因此系统在与低值分子/分母组合的有理数相关的音调之间建立了强烈的联系。同样的情况也应该适用于许多其他对音乐有明显反应的动物。

问题是：在现代实践中，除了同度和八度之外，所有的音程都不是纯律的。当然，总是可以把任何乐器调成纯粹的纯律音程；这是一种方法，如今很少使用。不幸的是，这将使任意移调变得不可能：不同的调性不能等价。这个问题是相当根本的。很容易证明，试图实现移调等价性总是会导致无理数。例如，最常用的西方十二音十二平均律中的半音音程，其半音频率比等于方程半音¹² = 2的根。无理数只能近似于对应纯律关系的有理数。

 

也许解决这个不可避免的矛盾的唯一方法是使用动态音调技术，但这种很久以前就提出的方法仍处于初级阶段。值得注意的是，键盘的同构性被认为是动态音调的先决条件之一。

有趣的是，无理数存在的第一个证明通常归功于公元前5世纪的哲学家希帕索斯，他也提出了音乐音系的基础。

但是这种近似的误差有多大？平均律的音高与最接近的纯律关系有多大差异？我们可以通过与纯律的比较来获得一个很好的概念。这是我的计算结果：

1: C: error: 0 (unison, octave)
2: D: error: 3.91 (one full tone)
3: E: error: -13.7
4: F: error: -1.955 (perfect fourth)
5: G: error: 1.955 (perfect fifth)
6: A: error: -15.6
7: B: error: -11.7

误差以音分为单位显示。

误差问题在微音音乐中得到解决。另见新产品，微音织体。

它显示了纯音程是多么特殊：误差小于2音分。这些音程确实是基础。

我们注意到，这里由二级音代表的全音音程可以被认为是“第二基本音程”。值得注意的是，上面显示的相应误差恰好是纯四度和纯五度误差值的两倍。这是可以解释的：纯五度和纯四度之间的音程是一个全音，所以这个音程的误差是这两个纯音程误差的组合。

这些考虑为选择作为威基-海登布局基础的音程提供了一些解释，并支持了我在将音高与按键关联选择上的推理。在所考虑的音程中，只有三个接近纯律比值；而这三个都被用作键盘布局的基础。至于其他音程……听觉好的音乐家可以清楚地辨别纯律音程和平均律音程之间的差异。

这种平均律与纯律声音之间的矛盾是引导我们进入一个非常激动人心的话题的方面之一：微音音乐。这个话题太广泛，无法在本文中以任何认真的方式加以考虑。只说一点：在所谓的历史考证演奏（另一个最激动人心的话题）中，历史上的非平均律但基于纯律的调律形式被越来越频繁地使用。

轨道

音系中音程之间的关系可以用群论的术语来描述。为了我们的目的，将一个音程视为作用于一组音符的群作用将非常富有成果。

假设我们有一个群 G 作用于我们的音调集合。比如说，我们有一个音调集合 T，其中有元素 t，t ∈ T。让我们将某个群 G 的作用应用于给定的元素 t。结果元素的集合可能不是整个集合 T；一般来说，它将是 T 的某个子集。这个子集 Gt 被称为元素 t 的轨道（相对于给定的群 G）。

Gt = { gt | g ∈ G } ⊂ T

在我们的情况下，我们需要一些只有一个元素的群，这样每个作用就只是一个将某个音高移动给定音程的操作。当结果音高跨越八度时，我们应将其视为与原始八度中的音高相同。在编程中，这对应于运算符`%`，即模运算。换句话说，如果我们有一个接受一个音高作为参数并返回另一个音高的函数，那么函数和实际参数值的每个组合都会生成一组结果值。

另见：轨道和稳定子。

例如，如果作用集合只有一个作用，即移动一个全音的音程，那么音C会生成一个包含6个值的轨道：C, D, E。音F会生成另一个轨道：F, G, A… 但移动一个半音的作用将生成一个与所有12个音符的全集相同的轨道。

从此刻起，我们将只考虑群的最简单子集：通过加上一个固定音程在音符之间转换。对我们来说，有趣的是找出定义集合划分的音程。

这有助于理解术语“轨道”的用法。比方说，我们从C开始，依次加上一个全音的音程。我们可以无限地继续这个过程，但永远不会落在F上。如果我们从F开始，同样的事情也会发生：永远不会落在C上。这就是两个不同的轨道。

自然地，特殊的群是那些覆盖整个十二音集合的群。例如，如果群操作是将一个音高移动一个半音的音程，我们会绕一圈回到初始音符，周期为7。如果存在这样的周期，我将称之为轨道的周期。

让我们将所有音程根据每个音程所生成的划分归入子集：

1. 0: 12: 平凡轨道：生成12个各含一个音高的划分
2. 1, 5 (纯四度), 7 (纯五度): 生成1个包含所有12个音高的划分
3. 2: 生成2个各含7个音高的划分
4. 3: 生成3个各含4个音高的划分
5. 4: 生成4个各含3个音高的划分

我们不需要考虑其他音程（8个半音及以上），原因很简单：它们是我们已经考虑过的音程的转位。在半音圈的语境中，它们与较低的音程相同，只是逆时针计算而已。

因此，只有一个子集包含多个元素——即包含{ 1, 5, 7 }的那个。它也是唯一一个其作用能生成包含所有12个音高的轨道的子集。群作用是移动一个半音或两个纯音程中的任意一个——纯音程再次扮演了特殊的角色。

由纯四度或纯五度生成的轨道（两个相应的轨道仅在相位和运动方向上不同）在这张基于半音圈的图片中显示为蓝色的12角星。

它也很好地说明了一个众所周知的事实：整个十二音音系可以由基于4:3和2:3谐波比值的纯音程组合生成。不幸的是，这个或任何类似的操作都无法生成平均律，而平均律无法做到完美的纯律。（但是物理和数学的基本原理无所谓“幸运”或“不幸”，不是吗？:-))

这个简单的分类进一步揭示了纯音程的特殊和根本性质。请注意，一个半音实际上不那么根本。例如，使用八度内的24个音，如阿拉伯音系或现代24-TET，会改变平凡轨道，丰富音乐语言，但在音乐和声方面不会有太大改变。这是一个非常普遍的属性：任何可想象的音系的发明者，无论是否平均律，无论使用多少个音，都会首先考虑拥有纯音程并尽可能保持其纯粹性。

在我们的键盘上，水平行代表了由两个半音音程生成的两个轨道交错排列：一行是C-D-E，另一行是F-G-A，以此类推。两个纯音程代表对角线移动：如果我们向上左方向移动是5个半音，向上右方向移动是7个半音，分别是纯四度和纯五度。

垂直线定义了另一种轨道：直接向上或向下的垂直跳跃会落到更低或更高八度的同一个音符上。所有其他的轨道都可以通过以不同角度移动这个键盘来获得。我们可以移动半音、减三度或增三度等等。规则非常简单：沿着一条直线以固定的位移移动。

音系是格，而非序列

两个因素：八度等价性和音程对数尺度的算术级数定义了平均律音序的平移对称性。这样的序列（在编程中对应于一维数组）可以被看作是基于音高按某个固定音程移动的群的格。很明显，这个结构可以在任何维度的向量空间中通过选择某个基以及为每个基向量选择相应的音程/移位来再现。这样，几何上的平移对称性将与音高上的平移对称性相匹配。对于音乐应用，三维空间的特殊情况可能最有趣。在三维空间中，可能存在5种格类型，或17种晶体学对称群（壁纸群）。

一个二维晶格可以表示为一个周期性的镶嵌。因此，与音高相关联的键盘几何结构可以被归类为一种可能的镶嵌。这个概念本身，在我看来，是数学中一个令人惊叹的话题，首先是因为非周期性平铺的存在。但这里我们讨论的是更简单的周期性结构，具有平移对称性。

在某种意义上，建议的结构定义了与音程对称性相匹配的对称性。让我们考虑一下这种几何结构与威基-海登音符布局的几何结构之间的映射关系。

仅从这张图就可以看出，六边形平铺具有连续旋转π/3的对称操作。换句话说，有三个（如果考虑符号，则为六个）平移方向穿过两个相邻六边形的边。但是音高移动是不同的；它们在一个方向上对应±2个半音，在另外两个方向上对应±5或±7个半音。

我认为这是六边形键盘的缺点之一。它的对称性可以被认为是冗余的。如果键盘的方向未知，从几何形状上看不出音符是如何分配的。

这种模糊性在我们的几何结构中也存在，但只需一次测试即可解决：键盘可以正放或倒放。相对于垂直轴的对称性并非真的多余：具有±5和±7半音位移的对角线方向确实应该是对称的：从半音圈可以明显看出，+7个半音等价于-5个半音；而+5个半音等价于-7个半音。（我已经提到过纯四度和纯五度之间的互补关系。）

此外，我们的几何结构似乎更易于学习和识别。从这一点来看，我将我们的键盘结构视为改进的威基-海登布局。

现在，让我们仔细看看几何-音高空间中的平移对称性。

连接任意一对琴键的任何平移向量都会生成一条线，线上有以某个恒定音程周期性排列的音符图案。反过来，对于任何给定的音程，很容易找到一个向量，该向量对应于最近的琴键，其音高与起始音高形成该音程。例如，让我们考虑我们的威基-海登布局变体，并找到单个八度内所有12个音程的平移向量：

0. { 0, 0 } 或 { -6, 2 } 同度
1. { −2.5, 1 } 半音，小二度
2. { 1, 0 } 全音，大二度
3. { -1.5, 1 } 小三度
4. { 2, 0 } 大三度
5. { -0.5, 1 } 纯四度
6. { 3, 0 } 增四度
7. { 0.5, 1 } 纯五度
8. { −2, 2 } 小六度
9. { 1.5, 1 } 大六度
10. { -1, 2 } 小七度
11. { 2.5, 1 } 大七度
12. { 0, 2 } 纯八度

音程值以半音为单位计算，为简单起见，向量显示在欧几里得空间中，单位等于琴键的宽度/高度（假设琴键为正方形）。这些音程对应的周期性音高图案线在键盘上看起来是这样的：

请注意，八度音程的音符垂直地位于彼此之上，而8个半音的音程是唯一一个其对称平移向量超出当前八度的音程——其最近的音程是16个半音。

一个相当模糊的观察：基于更重要和更基本音程的方向倾向于更接近对角线，而其他方向则倾向于更接近水平线，当然不包括代表非常重要的大二度的水平线本身。

无论如何，基于这些音程中的大多数来演奏滑音是相当容易的——我们只需要以某个固定的角度移动，沿着音程图上显示的蓝线即可。我们的键盘引入了一整套新颖的滑音类型！

要很好地感受这个结构，最好练习使用应用程序软件，它以图形和声音两种形式呈现了该结构。

毛细胞共振

恐怕我关于3/2、4/3 和“第二基本”9/8根本性质的论证听起来仍像某种咒语。为什么频率比值中最简单的有理数会被我们的听觉系统以某种特殊的方式感知？对于2/1的比值（八度），这看起来很清楚：同一个共振器（比如毛细胞传感器）在其基频上共振，但也在其双倍频率——第二泛音上共振。难怪它能在每个频率和其双倍值之间建立强烈的联系。但对于分数有理数，如3/2或4/3，情况如何呢？共振器会对其基频的3/2频率做出反应吗？不完全是。这种关系稍微复杂一些，而且是间接的。由于这可能并非对每个人都100%清楚，我将尝试解释一下。

出生时，人类大约有3500个内毛细胞和12000个外毛细胞。由于内毛细胞作为声音探测器，这意味着原则上我们可以分辨多达3500种不同的音调。严格来说，我们可以听到（“听到”和“分辨”是两码事）一些超出所有这些传感器基频范围的声音。首先，传感器对泛音有反应。第二个方面要复杂得多：由于听觉系统的某种非线性，我们也能听到组合频率；这种现象相当复杂，与本文的范围无关。

要解释两个最基本音程（例如八度和纯“五度”）之间的强烈自然关联，只需要考虑不多不少3根毛发和5个泛音：

彩色线条显示了我们所有人对频率比为2:1（八度）和3:2（纯“五度”）的不同音乐声音之间所具有的强烈关联。此处及上文中，“五度”加引号是故意的：我想表明这只是一个约定俗成的问题。在不同的音系中，它可能根本不是五度。在这里，基本因素是频率比；而“度”和“音阶”在这个感知层面上根本不存在。

在这张图片中，只有三根弦代表内毛细胞。第一根和第二根弦分别显示了三次和两次，以展示不同的泛音，所以请注意左边的方括号：它们将同一根弦的图像放在一起。更重要的是，弦在物理上是不同的，在我的例子中，是长度不同，这决定了它们的基频：300、450和600赫兹。在图片中，我通过不同的弦长来表达弦的基频差异。确实，在其他因素相同的情况下，基频与弦长成反比，但最终的基频取决于多种因素的组合，如张力、粗细，更广义地说是几何形状。顺便说一句，如果有人指出我用弦的例子与耳朵的解剖结构不完全匹配，我会说那不重要。任何共振器都会有基频、第二、第三、第四泛音等等。这才是最重要的。

这个频率值的例子是为了展示逼真且易于感知的音调；这些频率是否与任何常规音符匹配并不重要；重要的是它们的基频分别是第一根弦频率的1、3:2和2，而第一根弦代表某个根音。

那么，让我们看看它在频率比3:2下是如何工作的。基频为300赫兹的第一根弦会对输入声信号的这个频率产生强烈共振，但也会对其第二和第三泛音，即600赫兹和900赫兹，产生稍弱的共振。但在同一只耳朵里，可以找到另一个共振器，其基频为450赫兹（300赫兹的3:2）——图中显示为第二根弦。重要的是它在其第二泛音900赫兹上共振——与第一根弦的第三泛音频率相同。因此，一根弦的第三泛音与另一根弦的第二泛音相匹配——又是3:2。这就是在某个频率和其3:2倍频率之间建立强烈关联的原因。

这大概是理解音乐如何运作所需的物理学、生理学和数学知识的最低限度了。

文化与物理

音乐及其理解是文化与完全独立于文化的物理客观规律的奇妙结合。一方面，没有文化，音乐作为人类生活的一种现象是不可能的。一首音乐作品之所以能与某种被不同人广泛共享的情绪相关联，仅仅是因为人们之前听过的其他音乐作品的积累。小孩子有相似感受的事实并不能反驳任何东西，因为这种文化的一些基本核心在极早期就被迅速吸收了。

但是音乐感知中哪一部分是纯粹自然的，独立于文化的呢？哦，这仍然是很大一部分。它包括可听的频率范围、可容忍的悦耳音色，以及非常重要的，对和声的基本感知。完全独立于任何特定文化，八度音程被感知为一组“几乎相同”的音。在西方实践中所谓的“纯”音程，将永远被感知为“悦耳”和“和谐”。在任何文化中，即使“纯四度”根本不是“四度”，“纯五度”也根本不是五度，这些音程将永远保持“纯粹”，仅仅因为它是由共振现象和人脑关联振荡器泛音的方式所定义的。

更好的记谱法

我们试图通过替代性半音键盘克服的问题之一是传统键盘的半音性不足。换句话说，它们过于暗示某种传统的自然音阶体系。

但是，传统的现代五线谱记谱系统同样会因为对同一自然音阶体系的偏爱而分散我们对音乐基本原理的注意力。是的，从形式上看，传统记谱法完全脱离了乐器，这非常好，但它带有某些偏向自然音阶的乐器（如钢琴）的明显迹象。平移对称性是假定的，但没有直接表达出来。因此，尽管为同构键盘、基于平移对称性的半音乐器创作的音乐可以用传统乐谱完美表达，但并不完全与之匹配。一种完美的记谱法确实需要是半音的，并且自然地显示平移对称性。

在我浏览过的众多替代性半音记谱系统中，保罗·莫里斯·克莱尔诺特的克莱尔诺特记谱系统给我留下了最深刻的印象。尽管它的原则看起来并非独一无二，但在我看来，它在视觉线索、最熟悉图形元素的使用以及图形紧凑性之间提供了近乎最佳的平衡。

其中一个令人印象深刻的图形元素是每个八度使用熟悉的五线谱，但是……中间的线不见了，所以这条线的片段只在有音符的地方添加。这为在五线谱内导航提供了更好的视觉线索。这个元素完全可以用在传统乐谱图形中，但可能没有人想到这个绝妙的主意。

该记谱法的另一个显著特点是其“6-6音高模式”。它与我们的键盘布局非常契合：对应于水平行的音符要么全是实心的（对于C-D-E行），要么全是空心的（对于F-G-A-B行）。这提供了额外的视觉线索，并有助于清楚地看到音符之间的音程。

换句话说，其图形与传统乐谱记谱法的区别，就像卓越的UI设计与普通UI设计的区别一样。我感觉，这个记谱法中许多思想的作者都深刻理解人类感知的认知方面、人机工程学、音乐演奏实践等等所有这些东西。

事实上，这是一个与本文主题无关的话题。我没有使用任何特定的音乐记谱法，也不打算在短期内在我软件中实现任何记谱法。同时，我只是想提请读者注意这种记谱法，以及一般的替代记谱法。我一直对古典记谱法和基本的教学技巧非常不满意。同时，在经历了一段音乐文化停滞和衰落的岁月后，我现在观察到的似乎是一场真正的音乐革命，特别是在历史考证演奏领域，人们对替代音符系统的兴趣重燃，许多历史乐器的复兴，以及另一方面，创新乐器的发展，还有一大批才华横溢的年轻音乐家的涌现。也许我的希望很天真，但我希望这最终也能在理论、记谱法和初学者教育方面将情况推向更好的方向。

编程

同构MIDI键盘应用程序

该应用程序以平行四边形格几何形状呈现了一个屏幕键盘，其方形按键的几何形状和布局接近于计算机键盘。音高集被分配给按键集：一个类似于威基-海登布局，另一个类似于扬科键盘。

键盘的中间部分被分配给实体计算机键盘的一组按键，如顶部图片所示。音频输出基于已安装的可用MIDI合成器。

该应用程序是基于 .NET WPF 的应用程序。为了最大化兼容系统的范围，它以“Any CPU”架构和 .NET v. 3.5 为目标。

特点

• 用户可以使用指点设备（鼠标、多点触控屏幕等）、物理计算机键盘或两者兼用来弹奏键盘。
• 在任何时候，键盘的音高分配都可以通过移调或选择一种音高模式来改变，一种是基于威基-海登布局，另一种是基于扬科键盘。
• 默认情况下，键盘覆盖从0到126的MIDI音符范围。通过移调+1或更多半音可以达到音符127。所有音符同时可见且可访问。
• 声音的音量由两个参数控制：正常操作的音量和用“Shift”键弹奏的“踏板”操作的音量。音量值可以随时更改，并在下一次激活键盘按键时使用。
• 所有可用的MIDI乐器按标准乐器组分组，并同时可见和可访问；当前乐器可以随时更改，并在下一次激活键盘按键时使用。
• 当按下“Ctrl”键弹奏根音时，和弦可以被自动构建和演奏。
• 当前和弦的配置可以随时修改。任何和弦音（相对于根音）都可以单独添加/启用/禁用。这样，所有共晓时期的和弦都可以使用。和弦的转位可以通过单独移动每个音符的音高来实现，向下移动一个八度；对于9到13度的音，可以移动一个或两个八度。
• 除了直接定义和弦外，当前和弦还可以通过在和弦预设列表中选择一个和弦来修改。
• 和弦预设列表可以随时通过添加/插入/移除/重置操作进行修改。
• 键盘按键可以用不同的方式标记。按键上的音符可以显示为MIDI音符（0到127的半音步数）或流行的拉丁字母记谱法（C-D-E-F-G-A-B）。此外，还有一个选项可以用相关字符标记与物理计算机键盘对应的按键。
• 当一个键被激活时，它会被高亮显示。
• 除了高亮显示当前活动的按键外，自动生成的和弦还可以选择性地用不同颜色高亮显示。可选地，这些和弦名称可以用数字记谱法标记和弦音的名称：2, 3（对于未变化的大三度用“m”），4, 5, 6, 7, 9, 11, 13，可能带有 - 或 + 符号。
• 设置组或单独的设置参数（当前乐器、移调、音量、当前和弦、和弦预设、布局和记谱法）可以单独重置或全部一起重置。
• 最后的设置集会被保存，并在应用程序启动时恢复。

MIDI API

对于本应用程序而言，仅MIDI功能就足够了。我没有使用任何第三方MIDI库，而是直接使用Windows多媒体API (WinMM)，如下面的代码片段所示：

public class SimpleApi : IDisposable {

// ...
   
   // basic functions are exported from 
   const string dllName = "winmm.dll";
 
   [DllImport("winmm.dll")]
   private static extern int midiOutOpen(out int handle,
      int deviceID, MidiCallBack proc, int instance, int flags);

   [DllImport("winmm.dll")]
   private static extern int midiOutShortMsg(int handle,
      int message);

   [DllImport("winmm.dll")]
   private static extern int midiOutClose(int handle);

   public void Dispose() {
      midiOutClose(handle);
   } //IDisposable.Dispose

// ...

   // then messages are composed using bitwise operations, according to MIDI standard:

   public void NoteOn(byte note, byte velocity, byte channel) {
      int command = note << 8 | velocity << 2 * 8 | (int)ChannelCommand.NoteOn | channel;
      midiOutShortMsg(handle, command);
   } //NoteOn

   public void NoteOff(byte note, byte velocity, byte channel) {
      int command = (note << 8) | (velocity << 2 * 8) | (int)ChannelCommand.NoteOff | channel;
      midiOutShortMsg(handle, command);
   } //NoteOff

} //class SimpleApi

除此之外，所有乐器都根据通用MIDI规范进行了规定和分组。分组的定义如下：

public enum Instrument {
   AcousticGrandPiano,
   //...
   Applause,
   Gunshot
} //Instrument

public class InstrumentGroup {
   internal InstrumentGroup(string name, Instrument first, Instrument last) { this.Name = name; this.First = first; this.Last = last; }
   public string Name { get; private set; }
   public Instrument First { get; private set; }
   public Instrument Last { get; private set; }
} //class InstrumentGroup

public static class InstrumentGroupSet {
   static InstrumentGroupSet() {
      var list = new InstrumentGroupList();
      list.Add(new InstrumentGroup("Piano", Instrument.AcousticGrandPiano, Instrument.Clavinet));
      list.Add(new InstrumentGroup("Chromatic Percussion", Instrument.Celesta, Instrument.Dulcimer));
      //...
      Groups = list.ToArray();
   } //InstrumentGroupSet
   public static InstrumentGroup[] Groups { get; private set; }
} //class InstrumentGroupSet

这些定义在代码中被用来自动创建一个乐器面板，其中使用WPF单选按钮来选择当前乐器。这些控件按照给定的顺序排列和分组，并一次性全部显示。这样的设计是为了尽量减少任何导航操作，专注于键盘本身的使用便利性。

键盘尺寸

我们需要多少个键和多少行键？这提出了一个非常有趣的组合学问题。我精确地选择了11行，其中最长的一行有35个键。为了增强对称性，“长”行（35个键）与“短”行（34个键）交错排列。这个选择绝非任意。它是相对复杂计算的结果。如果我们考虑以下硬性和软性约束条件，这个度量就会出现：

• MIDI接口提供了精确的128个半音音程的音符，从0到127。我们希望能够一次性访问所有或几乎所有的这些音符，而无需移调。这个范围也代表了大多数人或多或少能听到的频率。（实际可听范围明显更宽，但产生更低和更高音高面临许多技术限制。听到这些音高开始极大地依赖于听者的年龄和其他生理因素。）
• 首选的键盘形状应该是相对于垂直轴和水平轴都对称的。
• 在这个系统中，每一行都属于两个轨道之一，C-D-E 或 F-G-A-B。键盘的形状应该清晰地给出这个视觉线索。
• 两个轨道中每一轨的行在尺寸和水平对齐上都应该是相同的，以便在相同水平位置的音符之间有一个精确的八度音程。
• 键盘需要水平方向，并具有合理的宽高比。

有了这些，0到127个音符的表示就成了决定尺寸的因素。组合优化给出了最接近最优的结果，显示了0到126个音符。

构建

该应用程序使用所谓的便携式部署模型；它不需要安装。可以通过运行批处理文件“build.bat”而无需任何参数来从源代码构建。它基于.NET v.3.5或更高版本的安装，这通常预装在大多数Windows系统上，并包含所有必需的构建工具，而无需任何其他软件。

在极少数情况下，如果.NET安装在某个非标准位置，需要编辑文件“build.bat”以修改分配给变量`tool`的MSBuild路径。在更罕见的情况下，如果未安装.NET，则需要安装.NET v. 3.5或更高版本。

使用键盘

指法图

事实证明，人类的视觉感知和运动记忆在“2D”方面最强。将键盘赋予二维性使得音高之间的关系更加图形化且易于记忆。根据个人特点，有些人更擅长通过手指记忆，有些人更擅长通过图片记忆，但对于指法图来说，这是一回事。

图表总是以相同的方式阅读：从最低的线向上，然后在每条线内从左到右。如果按这个顺序弹奏琴键，它对应于音阶或琶音的升序。（当然，对于给定的键盘结构，总是可以给出一个例子，其中较高行的音高较低，但对我们的目的来说，这种情况没有用处。）

让我们看看我们的键盘布局如何帮助分析和更好地理解不同的音乐结构。指法图本身对于研究不是必需的，但它们可以帮助我解释问题。

调式

让我们以我们基于威基-海登布局的矩形键盘布局为例，试着检验它是否有一些优点。让我们从现代的调式开始，它们基于现代的自然音阶。有时这些调式被称为“自然的”，但对我来说，它们并不比许多其他调式更自然。它们只是与共晓时期的自然音阶体系，即其当今形式，有最强的亲和力。

它们在这里：

1. 伊奥尼亚调式 (Ionian): C-D-E-F-G-A-B-(C) => 1 2 3 4 5 6 7 8, 大调音阶
2. 多利亚调式 (Dorian): D-E-F-G-A-B-C-(D) => 1 2 ♭3 4 5 6 ♭7 8
3. 弗里吉亚调式 (Phrygian): E-F-G-A-B-C-D-(E) => 1 ♭2 ♭3 4 5 ♭6 ♭7
4. 利底亚调式 (Lydian): F-G-A-B-C-D-E-(F) => 1 2 3 ♯4 5 6 7
5. 混合利底亚调式 (Mixolydian): G-A-B-C-D-E-F-(G) => 1 2 3 4 5 6 ♭7
6. 爱奥利亚调式 (Aeolian): A-B-C-D-E-F-G-(A) => 1 2 ♭3 4 5 ♭6 ♭7
7. 洛克里亚调式 (Locrian): B-C-D-E-F-G-A-(B) => 1 ♭2 ♭3 4 ♭5 ♭6 ♭7

在这个列表中，数字代表相对于大调音阶的主音级数。换句话说，对于伊奥尼亚调式，序列从该音阶的第一级音C开始；对于多利亚调式，从第二级音D开始，依此类推，如指法图旁边所示。

这些调式由相同的音符组成。那么，为什么它们听起来不同呢？中世纪和文艺复兴时期的西方教会作家，可能沿袭了古希腊音乐家和理论家的做法，为他们的调式赋予了深刻的情感诠释（与现代的有些不同）。

这并非因为顺序——调式被用在顺序不同的旋律中。它们只是以不同的调性展示，以传统方式说明其生成原理。传统上，调式是在同一调性下进行比较，或者等价地，指出它们与伊奥尼亚调式的区别。我们可以取某个固定调性下的调式，通常是C调，然后通过变音某些音级来创建其他调式。但并非所有变音都被认为是“自然的”，只有那些通过上面列表中明显的循环重排生成的变音才是。要看到这些变音，只需在C-D-E…调上构建调式，然后将它们移调到同一调性。循环重排只是将其他音符推移一两个半音，所以最右边的音会滚动到下一个八度。这个操作被称为音程的转位。当我们将转位的结果移调到同一调性时，我们就得到了变格调式。由于我们键盘布局的[平移对称性]，移调简化为将任何指法图移动到任意位置，同时保持键位之间相同的几何关系。这就是为什么我从不在我的指法图中显示根音（它总是最低行的最左边的键）：在计算术语中，指法图是不变的。

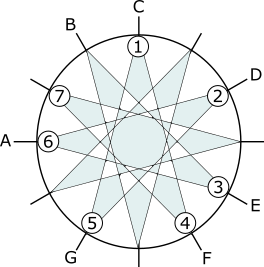
“音乐变形五角星”

让我们看看我添加到半音圈中的星形。

我这样连接五个音符是为了表达以下想法：1) 在C调中，它是一个相对于C轴对称的几何图形；2) 使用的音程只有F和G这两个最基本的纯音程，以及一个全音的“第二基本”音程，对于D是顺时针计算，对于♭B是逆时针计算。如果一切都如此和谐对称，我们可以预期这个结构在音乐中会扮演某种特殊的角色。

事实上，这个结构被称为大调五声音阶，如果从♭B顺时针数到G。由于调式和音阶传统上是从C开始的序列来描述的，让我们通过将头部倾斜-π/3（或想象这样做）来进行移调，使D轴成为对称轴。然后我们会得到序列C-D-E-G-A。这就是它在我们的键盘上可以弹奏的方式，完全具有相同的星形对称性：。

毫不奇怪，这个结构在音乐中也扮演着基础性的角色，在某些方面，甚至比传统的西方小调和大调更为基础。认为它是一个省略了某些音级的“普通”七声音阶将是一个常见的错误。相反，它是一个主要且独立的结构。对西方耳朵来说，它可能听起来像“中国风”（并且确实在中国音乐中使用），但实际上它对于许多国家的民间音乐以及灵歌、福音音乐、爵士乐……嗯，读这篇文章比列举出来更容易。

现在我们可以做与七音调式相同的练习。显然，可以考虑五种不同的五音调式。每种这样的调式都可以通过从C-D-E-G-A中的一个键开始，并循环移动其他键来获得。然后，为了比较，所有得到的序列都可以移调到同一调性。

现在我们可以尝试揭开一个谜团。上面列出的“自然调式”中有一个也很特别。奇怪的是，它不是传统的“C-D-E-F-G-A-B”伊奥尼亚调式，而是混合利底亚调式。出于某种原因，它与现代数字和弦记谱法有关。让我们试着解释一下。

混合利底亚调式的奥秘

与音阶或调式术语相比，和弦术语中存在一些明显的不一致之处。例如，当讨论共晓时期的大调音阶时，B被称为第7级音。当构建一个和弦并使用第7和弦音时，♭B被视为未变化的七度音，其表示不带任何变音记号，如♭或-；这只是记谱法的特殊性之一。然而，我只能推测，这也与某些和弦音和调式旋律音的功能有所不同有关。在现代实践中，这样的七和弦通常被称为属七和弦（见顶部图片中的♭B），并被视为“所有七和弦中最重要的一种”。降B被用来给和弦增加额外的动感，使其更具不协和和“引导性”的特点，因为它通常开启一个不同的音乐乐句循环。这种非常基本甚至乏味的音乐措辞手法，尤其在现代民间或流行音乐中很典型，在早期使用中却非常罕见，即使是在共晓时期的早期，即接近19世纪之前的某个时期。在那时，降七度被认为是装饰音或非和弦音，因此现代的C-E-G-♭B“属七和弦”甚至不会被认为是一个有效的和弦。

同时，减七度听起来相当和谐，这与我试图解释的与五声音阶系统相关的原因有关。事实上，和谐价值与主观的“协和”或“不协和”品质之间的相关性并非那么直接；这种感知也高度依赖于文化因素。

有趣的是，围绕着B和♭B这两个音符，存在着一些历史/文化上的特殊性。在一些欧洲国家，这两个音符有不同的名称和表示字母。在“我们的”记谱法中，B表示相对于C音程为11的si（ti）音，而♭B表示音程为10的si/ti-bémol/bemolle/flat。此时，为了避免对哪种记谱法是“正确的”做出任何假设，让我使用无歧义的名称si和♭si。在某些文化中，si被表示为H，而♭si被表示为B。H记谱法通常被称为“德式”，但其使用范围要广得多。我个人也更习惯用H表示si，而不是B。即使在同一个国家，出版物中也可以找到B和H两种记谱法，最常见于流行音乐。如果找到H，意思就很清楚，但如果找不到，如何理解“B”呢？想象一下读者的困惑，他们大多是业余音乐家，不得不从上下文中推断其含义。

无论如何，我们可以想象造成这种混乱的根本原因可能是什么。原因是，在C调中，如果将♭si视为C向下移动一个全音（在半音圈上逆时针计算），它形成了一个根本上和谐的音程，而si则不是。但是未变化的si在C大调音阶中扮演着其导音的角色。

所以，回到♭si（♭B）作为七级音……让我们总结一下。在C大调音阶中，七级音是si（B）。另一个自然调式音阶，其中所有音符都相同，除了B被降为♭B的，只有一个，即混合利底亚调式。最后，另一个将♭si（而非si）视为C调七级音的地方是现代字母数字和弦记谱法。即使当和弦被视为C调大七和弦时，与C大调音阶相反，七级音是♭si（而非si）。

相当简单的观察揭示了现代和弦分类是如何建立的。它可以表示为以下步骤的序列：

• 取与混合利底亚调式相对应的音符序列。为简单起见，我们考虑C调，那么它将是 C-D-E-F-G-A-♭B。
• 从三和弦开始，每隔一个音取一个：1-3-5。在C调中，我们得到C-E-G，大三和弦。
• 可选地加入七度音，这样我们就得到了C-E-G-♭B。
• 对于这些音符中的任何一个，将除一级音外的任何一个音级变动一个半音。请注意，减七度将变成六度，但在这种情况下，我们最好将六度视为“在七度音区域内”的音符。还要注意，减三度对应于“小调”的概念。
• 基本上，这完全涵盖了八度内的所有和弦，不计算转位和相当特殊的“挂留”和弦，我将不得不在另一处单独解释。
• 从这一点出发，我们可以选择性地添加九度、十一度或十三度音，它们本质上是跨八度的二度、四度和六度音。在C调中，如果这些音符没有变化，它们就是D、F和A。
• 可选择地，将9度、11度或13度音（如果存在）中的任何一个向上或向下变动一个半音。同样，虽然9度音可以减或增，但11度音只能增，13度音只能减，否则变动会落入对应于我们调式不同音级的区域。

了解了这一切之后，让我们深入了解和弦的结构。

和弦

我对和弦结构的解释将基于应用程序UI中标示为“和弦”的部分。所需和弦结构的选择是通过勾选某些单选按钮或复选按钮来完成的。

和弦结构

这是和弦结构在用户界面中的表示方式：

如果还不太清楚，让我们澄清一下它的含义：

用/2	−	纯	+	默认值
x	13−	13		x
x		11	11+	x
x	9−	9	9+	x
x	6	7	7+	x
	5−	5	5+	5
2	m	3	4	3

这个表格应该从下往上阅读和使用。这是因为我试图在键盘布局和记谱法中都传达音“高”的概念：更高的音高显示在更高的位置。和弦结构是基于上面解释的步骤。

我想这里的一切应该都很清楚，除了第一列和最后一行。

• 数字1到13表示可以与和弦根音关联的混合利底亚调式的音级。
• 数字1被省略了，因为它是和弦的根音。
• + 或 - 分别表示 ♯ 或 ♭，即升号或降号，一个半音的变音，分别向上和向下。
• “m” 只是指 3−；它代表了共晓时期术语中“小调”和声的概念。
• “x”代表表格行中没有任何音符。
• 一组默认值“1/3/5”构成一个大三和弦。

一级音没有显示，因为它是根音，总是被弹奏。也可以不弹奏它，但那就意味着是另一个和弦，有另一个根音。

在最后一行，放置了三和弦的二度和三度音，但我也特意将四个传统三和弦与 sus2 和 sus4 合并在一起，仅仅是为了节省应用的屏幕空间。在 sus2 和 sus4 和弦中，通常的三度音被省略，并分别由二度音或四度音替代。通过这样做，我也避免了三度音缺失的选项，因为三度音确实可以缺失，但和弦中总是会存在二度、三度或四度音。因此，在最左边的列中，“2”取代了“x”的位置，这让列表头看起来有点奇怪。

类似地，这也解释了为什么某些音级缺少 + 或 - 变化音：由于基础音阶系统（米克索利迪安调式）的全音阶特性，一个半音的变化可能会使其落到另一个音级上，因此它会有一个不同的名称，并在结构中占据不同的位置。

前两行可以产生所有三和弦。从根音 1 开始，默认的半音音程为：4-3（大三和弦），3-4（小三和弦），3-3（减三和弦）和 4-4（增三和弦）。在传统的数字和弦标记法中，“纯”位置（三度和五度）的三和弦音符从不显示。因此，如果根音是 C，和弦名称分别是 C、Cm、C5−（有时是 C°）和 C5+（有时是 C+）。

但是，为了方便和节省一些屏幕空间，我还在三度音的那一行添加了两个“挂留”和弦，因为当它们与五度音组合时，会产生 sus2 或 sus4 和弦，这与经典的三和弦是互斥的。在纯五度的情况下，它们的音程分别是 2-5 (sus2) 和 5-2 (sus4)。我们先来看看这两个和弦。

我认为“挂留”和弦被严重低估了，甚至被误解了。让我们看看我们的键盘布局如何揭示它们的根本性质：这是 sus4 和弦： 这是 sus2 和弦：。它们的指法占据了我们的“基本按键三角区”，原因显而易见：sus4 和弦使用了对应于完全音程的音符，它也被称为四度和声和弦。至于 sus2 和弦，将其移调 +5 个半音（同样是完全音程）后，如果把五度音当作一度音，会得到相同的对称结构，因此它们是相互共轭的；这种对称性在我们的键盘指法图上得到了有力的印证。有趣的是，在整个共晓时期，这种没有三度音的和弦并不被认为是和弦：在某个时期之前，我们的二度音或四度音会被认为是和弦外音。

现在，让我们来看看基于大三度或减三度的经典三和弦：大三和弦 ，小三和弦 ，减三和弦 ，增三和弦 。

像小三和弦和大三和弦这样基础的和弦，看起来如此不对称，可能有点奇怪。但如果没有它们在平行大小调中的*互补*对应和弦，它们本就不该是对称的。在下图中，前三个较低的音符（黄色）构成大三和弦，其后是其平行小调的小三和弦（蓝色）。

。例如，这可以是 C 大三和弦 + Am 小三和弦。现在它已经尽可能对称了。:-)

让我们继续往上看。实际上，所呈现的方案涵盖了数字和弦标记法中常见（以及不那么常见）的大多数和弦。再往上一行是六度/七度音。它们被合并在一起的原因很明显：七度音可以增高，称为 7+，但将其降低就会变成六度音。它们的指法如下：六度 ，七度 和增七度 。

九度、十一度和十三度音，本质上就是高一个八度的二度、四度和六度音。

有些标记元素容易混淆，所以我需要解释一下。一个很简单：“maj” 或 “M” 表示 7+。另一个，“dim” 有时会令人困惑。实际上，它是 m5−/6，指法为 。这种命名的混乱在那篇文章中有所解释，该和弦被归类为“减七和弦”—— 不太清楚为什么不叫“减六和弦”。非常不幸的是，这个非常特殊且重要的和弦在命名和标记上陷入了这种混乱。因为它由四个音构成，每个音之间相隔均匀的 3 个半音，恰好是整个半音圈的四分之一，所以只有四个具有不同根音的此类和弦——其他的都是彼此的转位。这个和弦典型的音乐语义（或功能）也很有趣：粗略地说，它可以听起来刺耳或非常旋律化，“小调感”或“大调感”，这取决于音乐*乐句*的上下文。请在此章节中阅读关于这个主题的更详细的看法。

另一个令人困惑的地方是省略规则。从七度音开始的较高音级，如果 1) 它们处于“纯”位置，且有更高的音级存在，那么它们就会在标记中被省略。例如，C9 和 C7/9 意思相同——七度音实际上是演奏了，但在标记中被省略了。另一方面，变化的七度音则需要明确标出：C7+/9，C7-/9。但是，如果从七度音开始的某个音级没有被实际演奏，那么更高的音级会带有前缀“add”。例如，Cadd9+ 或 Cadd9 意味着九度音是在大三和弦之上演奏的，但七度音并没有发声。

如何使用它呢？首先，如果一个音符带有 `Ctrl+` 前缀，应用程序会自动生成和弦。除了上面描述的之外，还可以通过对和弦的每个音符使用分频器（UI 中的 `/ 2`）来构建所有和弦的转位。

那么，我们能用它做什么呢？首先，该应用程序帮助用户使用上述结构来构建和弦，其 UI 部分与上面显示的表格非常相似。然后，当用户通过 `Ctrl+音符` 弹奏根音时，可以自动构建和弦。当使用屏幕键盘弹奏和弦时，和弦音符可以被自动定位并在屏幕上高亮显示。此外，屏幕上的按键还可以选择性地显示每个和弦音符的数字标记（“2”、“m”（小调）、“3”（大调）、“5+”、“7”、“7+”等）。无论音符是通过物理计算机键盘弹奏，还是使用鼠标、轨迹球或触摸屏弹奏，都没有区别。

这可以用来学习和弦结构，并为每个和弦找到可能方便的指法。由于每个音符通常可以在多个位置弹奏，屏幕上的*和弦定位器*会优化备选位置的选择，其使用的简单原则是：几何上离和弦根音键位置更近的按键会被优先选择。此外，和弦音符（除根音外）还可以选择性地用黄色高亮显示。

和弦也可以通过键盘手动输入。学习自动生成的和弦有助于理解和弦结构并习惯于弹奏它们。然而，有一个问题……

键盘的反击：按键冲突问题

这个问题可以被描述为缺少 n 键无冲突（n-key rollover）功能。这意味着键盘无法正确处理多个同时按下的按键。在写这篇文章的时候，我正在我的笔记本电脑上使用我的应用程序。如果我按住一行中的四个键，任何相邻的键都不会向计算机发送按键信号。这与硬件、键盘电路（缺少*隔离二极管*）和控制器有关，是降低键盘成本和设计复杂性的结果。

如果不去寻找并购买一个更好的键盘，我们对此无能为力。我们可以像柳博奇卡那样，只弹奏琶音。另一种处理和弦的方法是使用和弦生成功能，尤其是和弦预设功能。

另一个问题与平移对称性的概念有关。严格来说，就标准计算机键盘而言，它们并非那么对称——其布局有相当大的扭曲。“Q”行相对于“A”行的偏移，并不像“A”行相对于“Z”行那样对称。对于真正的演奏来说，这将是一个严重的麻烦，但毕竟，我们只是在学习……

和弦结构并非唯一

由于转位的可能性，作为一个和弦演奏的一组音符与和弦结构之间并非一一对应。更确切地说，从音符集合到和弦结构的映射是一个满射函数。

例如，C-♭E-G-♭B 这组音符可以归类为 Cm7，但也可以看作是 ♯D 的大三和弦加上六度音，即 ♯D6。

这就是为什么任何提供“和弦命名”功能的正经软件通常会提供不止一个答案选项。严格来说，并不总是可能将一组音符“正确”地表示为一种和弦结构。然而，通常可以根据和弦在某个音乐乐句中的功能来做出选择。*通常*，一个孤立的和弦在脱离上下文的情况下没有明确的意义。

和弦名称

不同来源使用的和弦名称非常混乱，在任何地方都没有官方标准，而且在我看来，不应过于当真。只有基于乐谱的记谱法可以被视为相当稳固的业界标准，所以无论如何都应该学习它们。有时，读者需要进行猜测，并从上下文中弄清楚记谱法到底是什么意思，严格来说，这只有在读者熟悉这首音乐时才可能。我已经提到，“dim” 有时可以被理解为减三和弦或 m5−/6。此外，“maj” 通常表示 7+，但有时也表示“大调”。另一个模糊的来源是符号‘°’。它可能表示减三和弦，但有时也用于“dim”。另外，有时会用特殊符号 Ø 来表示所谓的“半减和弦”，它与“dim”相似，但其七度音不是减音。并且，在出现字母“B”的情况下，如果假定使用德制 H 记谱法来表示 si 音，情况可能会变得一团糟。希望所有这些混乱主要发生在读者熟知的流行音乐作品的简化出版物中。

此外，记谱法中的和弦名称通常会被“优化”以使其更短。为此，音符的顺序可能会被重新排列，以最小化分隔符（通常是‘/’）的数量。例如，在“C7+5”中，7度音在5度音之前只是为了避免额外的分隔符“+5/7”。嗯，也许甚至“57”会更清晰：一些人把 + 或 - 写在数字后面，一些人则写在前面并坚称如此，以匹配标准乐谱中 ♯、♭ 和 ♮ 的前缀形式。这又造成了另一种模糊性。

我提到所有这些，主要是为了指出在应用程序的用户界面中，和弦名称只出现在一个地方：和弦预设。

和弦预设

预设中和弦名称的目的与和弦标记的通常用法有所不同。所以，我的命名方式与人们在和弦标记中通常写的有些不同；例如，使用 ‘/’ 分隔符是为了避免阅读时的歧义，尽管实际选择的和弦也可以在预设的左侧读到。

我希望和弦预设的用户界面部分是不言自明的。

我只想解释一下默认预设中和弦的顺序。预设的目的是为了快速选择要用“Ctrl”键自动弹奏的和弦。例如，在一个典型的小调和弦进行中，用户可以将预设选择保持在“小调”标记上，然后快速切换到“7”或“大调”，这些是在此类进行中最常用的。用户可以根据当前需要快速修改预设，并且这个选择会在应用程序的会话之间保持。

未来工作

一些进一步的想法包括：

• 用户自定义键盘布局。这对于使用与美式英语键盘物理布局不同的用户可能很有用。
• 键盘分割。可以定义键盘上的一个或多个区域进行单独设置：每个区域的乐器选择、音量和移调都可以不同。
• MIDI 录制。我不确定这是否会是一个有价值的选项。毕竟，该应用程序不能作为一种严肃的乐器来进行真正的表演。相反，它可以作为一个学习和实验的工具。
• 涵盖其他替代音律系统，例如19-TET或31-TET，将会非常有趣且富有成效（目前已实现；见下文）。
• 另一种微分音方法是使用动态音调，可以明确地（通过一些额外的控件）或在某些触发器（在音乐行进过程中出现某个和弦或序列）上根据表演前创建的预设进行更改。
• 使用 Web 浏览器实现的Web Audio API来代替 .NET，以实现终极的跨平台兼容性（目前已实现；见下文）。

未来已来

在撰写本文时，上述一些计划已经实现。一个名为Microtonal Fabric的新产品已经诞生。它是一个平台和一组可在 Web 浏览器中运行的应用程序。顾名思义，它是***微分音***的，并提供了一些有趣的额外功能，例如不同音律系统的音调/和弦比较。令人惊讶的是，由于上面讨论的键盘布局，为一种音律系统习得的基本演奏技巧和技术可以立即应用于其他音律系统。

目前支持以下音律系统：

• 纯律（仅由 Multi-EDO Chromatic Lattice 应用程序在半音圈键盘上呈现）。
• 共晓时期系统 12-EDO（十二平均律）。
• 19-EDO（十九平均律）。
• 31-EDO（三十一平均律）。.

29-EDO（二十九平均律）由一个独立的应用程序支持（源代码：“29-EDO”）。这个应用程序更为先进，目前在著名的国际布莱宁音乐学校定期用于音乐教学。它值得单独写一篇文章来介绍。

可以使用 Microtonal Playground（源代码：“playground”）创建任意的音律系统。

这些应用程序支持标准触摸屏。使用触摸屏，可以用十个手指弹奏任何和弦、滑音（重要）以及任何组合。因此强烈推荐使用触摸屏。没有触摸屏的用户仍然可以使用鼠标/触摸板，以及在特殊情况下使用计算机键盘进行演奏。

整个项目可以在 GitHub 上找到。相关的 CodeProject 文章也已发布。

目前在 Microtonal Fabric 中可供直接使用的应用程序可以在 Microtonal Fabric 主文档页面上找到。人们可以直接在 Web 浏览器中试用这些应用程序并演奏音乐。

本文讨论的应用程序名为 Multi-EDO Chromatic Lattice，可以在这里演奏。

本文讨论的另一个应用程序是用于微分音系统比较的应用程序。

结论

当然，最终，乐器音高的控制器如何排列并不重要。只要有其他的易用性和便利性，任何东西都可以被学习并用于表演。但这些排列和布局或多或少能够暗示音与音之间的某些关系。我们有很长的历史来观察不同新兴乐器如何影响音乐本身。那么，与传统键盘相比，我们为什么不能设计出一些能更清晰地表达最根深蒂固关系的东西呢？

乐器的发展，就像文明产生的任何其他事物一样，受到两种力量的驱动：习惯和观念。无论是好是坏，在绝大多数变革中，习惯都占据了压倒性的优势，而观念则需要克服极其困难的障碍才能铺平道路，而这些障碍大多也与习惯有关——你可以称之为“教育”，但我更喜欢用“训练”这个词，以区别于本质上总是概念性的教育。

看起来，电子时代将消除许多障碍，为许多新颖的想法开辟道路。但我们并没有观察到这一点。毕竟，像按键位置这样的东西并不受限于机械杠杆的定位。然而，我们现在使用的标准计算机键盘只是模仿旧式打字机键盘；其原因是可以解释的。至少在一个方面，这种配置，通过一系列纯粹的巧合，提出了一个简单但概念上先进的想法：开发一种能够高度暗示音乐和声基本关系的全新音乐键盘。

我将非常感谢任何问题、指正、意见，当然还有批评。