关于JavaScript中的PA = LU的注意事项
这是一篇关于 Javascript 中 LU 分解的说明。
引言
这是一篇关于 Javascript 中 LU 分解 的说明。
背景
纵观人类历史,线性联立方程组曾经并且将继续对我们的日常生活产生如此重大的影响。它是解决大量更复杂数值计算问题的核心组成部分。线性联立方程组的解可能是人类历史上研究最多的课题。
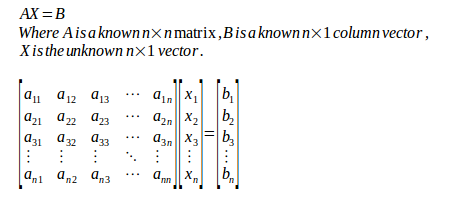
- 伟大的卡尔·弗里德里希·高斯——高斯研究过这个课题,并以他的名字命名了“高斯消元法”;
- 伟大的艾萨克·牛顿——牛顿也研究过这个课题,剑桥大学于 1707 年出版了他的笔记,名为《算术通论》。由于牛顿比高斯年长一百多岁,他显然更早接触了这个课题;
- 不太出名的刘徽——刘徽也研究过这个课题,并写了一本书《九章算术》。由于刘徽比牛顿年长一千多年,他显然更早接触了这个课题。鉴于部分章节大约写于公元前 150 年,人类可能在耶稣基督诞生之前就已经研究过线性联立方程组的解了;
- 伟大的艾伦·图灵——图灵在数字计算机的背景下研究过这个课题。他发明了基于著名的“高斯消元法”的“LU 分解”,这非常适合用计算机解决线性联立方程组。
求解线性联立方程组是一个如此重要的课题,同时也是一个相对容易的课题。这是防止阿尔茨海默病的一些日常锻炼的好机会。因此,让我们在 Javascript 中实现著名的 PA = LU 算法,并从中获得乐趣。

附带的是一个 Java Maven 项目。但你不需要 Java 也能运行它。该示例旨在在 Web 浏览器中运行,因此重要的文件是 Javascript 和 HTML 文件。由于“index.html”文件引用了一个 CDN,因此您需要一台能够访问互联网的计算机才能加载它。
算法
在数字计算机的背景下,“高斯消元法”的标准实现是由艾伦·图灵引入的“LU 分解”。通常,在 LU 分解中我们需要进行主元操作。但出于简化的原因,我们首先来看一下基本 LU 分解的步骤。
基本 LU 分解
对于给定的矩阵 A,LU 分解的目标是找到一个下对角矩阵 L 和一个上对角矩阵 U,使得 A = LU。

为了找到 L 和 U,我们首先将 L 设置为单位矩阵,U = A。

作为使 U 矩阵成为上对角矩阵的第一步,我们需要消除第一行下方的所有第一列条目。

不难验证,经过这些操作后 A = LU 仍然成立。LU 分解的第二步是消除第二行下方的第二列条目。

我们可以继续这个过程,消除对角线以下的条目,以完成 A = LU 的 LU 分解。
PA = LU
在许多情况下,我们并不那么幸运,以至于所有对角线条目在所有步骤中都不是零。即使矩阵 A 是非奇异的,也可能存在零对角线条目。在这种情况下,我们需要交换 U 矩阵中的行,以创建一个非零对角线条目。行交换的过程称为“主元”或“置换”。

为了在交换行后保持等式,引入了一个置换矩阵 P。在 LU 分解的第 0 步,P 矩阵初始化为单位矩阵。
- 当对角线条目为 0 时,需要进行置换,因为它是 LU 分解过程中的除数;
- 当对角线条目非零时,需要进行置换以获得数值稳定性。这是因为如果除数太小,数值误差可能会显著增大。
在上面的例子中,我们将扫描 u33(2) 到 un3(2) 的所有条目,以找到绝对值最大的条目,在本例中为 up3(2)。我们将交换 U 矩阵中的第 3 行和第 p 行,将 up3(2) 移到对角线上。为了保持 PA = LU,我们需要同时修改 P 和 L 矩阵。为了看到我们如何修改 P 和 L 矩阵,让我们将 L 和 U 矩阵细分为块矩阵。


从上面的块矩阵运算可以看出,交换 U 矩阵中的第 3 行和第 p 行只会影响矩阵乘积 LU 的下半部分。考虑到这一点,我们可以利用以下事实来弄清楚如何修改 P 和 L 矩阵。

如果您仔细查看块矩阵,不难发现,为了保持 PA = LU 并将 up3(2) 移到对角线上而进行的操作如下。
- 交换 U 矩阵中第 3 行和第 p 行,针对第 3 列到第 n 列;
- 交换 L 矩阵中第 3 行和第 p 行,针对第 1 列到第 2 列;
- 交换 P 矩阵中第 3 行和第 p 行。
无论对角线条目是否为零,为了在 LU 分解的每次消元步骤中获得更好的数值稳定性,通常都需要进行主元操作。
PA = LU 的伪代码
总之,带有部分主元 PA = LU 的 LU 分解算法可以通过以下伪代码进行描述。

Javascript 实现
Javascript 中的矩阵表示

在我的算法实现中,Javascript 中的矩阵是通过数组的数组实现的。
- 数组第一层的每个条目代表矩阵中的一行;
- 数组第二层的每个条目代表行中相应列的条目。
因为我使用的是 Javascript,所以数组元素的索引都是从 0 开始的。
实用工具
为了使工作更加轻松,我实现了一个实用对象,我将在算法实现中广泛使用它。该实用对象公开了几个方法。每种方法的目的都可以通过其名称轻松识别。
// Utility
let MatrixUtil = function() {
let Identity = function(dim) {
let I = [];
let i, j;
for (i = 0; i < dim; i++) {
let r = [];
for (j = 0; j < dim; j++) {
r.push((i == j)? 1: 0);
}
I.push(r)
}
return I;
};
let Clone = function(M) {
let C = [];
let i, j;
let rc = M.length;
for (i = 0; i < rc; i++) {
let m = M[i];
let r = [];
let cc = m.length;
for (j = 0; j < cc; j++) {
r.push(m[j]);
}
C.push(r);
}
return C;
};
let Transpose = function(M) {
let C = [];
let i, j;
let rc = M.length;
let cc = M[0].length;
for (i = 0; i < cc; i++) {
let r = [];
for (j = 0; j < rc; j++) {
r.push(M[j][i]);
}
C.push(r);
}
return C;
};
let Sum = function(A, B) {
let C = [];
let i, j;
let rc = A.length;
let cc = A[0].length;
for (i = 0; i < rc; i++) {
let r = [];
for (j = 0; j < cc; j++) {
r.push(A[i][j] + B[i][j]);
}
C.push(r);
}
return C;
};
let Subtract = function(A, B) {
let C = [];
let i, j;
let rc = A.length;
let cc = A[0].length;
for (i = 0; i < rc; i++) {
let r = [];
for (j = 0; j < cc; j++) {
r.push(A[i][j] - B[i][j]);
}
C.push(r);
}
return C;
};
let Multiply = function(A, B) {
let C = [];
let rCount = A.length;
let cCount = B[0].length;
let i, j, k;
for (i = 0; i < rCount; i++) {
let r = [];
let ra = A[i];
for (j = 0; j < cCount; j++) {
let cell = 0;
for (k = 0; k < rCount; k++) {
cell = cell + ra[k] * B[k][j];
}
r.push(cell);
}
C.push(r);
}
return C;
};
let Round = function(M, decimal) {
let C = [];
let rc = M.length;
let cc = M[0].length;
let i, j;
for (i = 0; i < rc; i++) {
let r = [];
let rm = M[i];
for (j = 0; j < cc; j++) {
r.push(Number(rm[j].toFixed(decimal)));
}
C.push(r);
}
return C;
};
return {
Identity: Identity,
Clone: Clone,
Transpose: Transpose,
Sum: Sum,
Subtract: Subtract,
Multiply: Multiply,
Round: Round
};
}();
PA = LU
LU 分解算法实现在构造函数“LU”中。
let LU = function() {
let self = this;
let getMaxEntry = function(cIdex) {
let U = self.U;
let maxIdex = cIdex, max = Math.abs(U[cIdex][cIdex]);
let dim = A.length, i;
for (i = cIdex + 1; i < dim; i++) {
let next = Math.abs(U[i][cIdex]);
if (next > max) {
max = next;
maxIdex = i;
}
}
return maxIdex;
};
let pivot = function(p, n) {
let dim = self.A.length;
let U = self.U, L = self.L, P = self.P;
let temp, i;
// U
for (i = p; i < dim; i++) {
temp = U[p][i]; U[p][i] = U[n][i]; U[n][i] = temp;
}
// L
for (i = 0; i < p; i++) {
temp = L[p][i]; L[p][i] = L[n][i]; L[n][i] = temp;
}
// P
temp = P[p]; P[p] = P[n]; P[n] = temp;
};
let eliminate = function(p) {
let dim = self.A.length;
let U = self.U, L = self.L;
let i, j;
for (i = p + 1; i < dim; i++) {
let l = U[i][p] / U[p][p];
L[i][p] = l;
for (j = p; j < dim; j++) {
U[i][j] = U[i][j] - l * U[p][j];
}
}
};
let setA = function(A) {
// A is a square matrix
let dim = A.length;
self.A = A;
self.U = MatrixUtil.Clone(A);
self.L = MatrixUtil.Identity(dim);
self.P = MatrixUtil.Identity(dim);
return self;
};
let PLU = function() {
let A = self.A;
let dim = A.length;
let i, j, k;
for (i = 0; i < dim - 1; i++) {
// Find the max entry
let maxIdex = getMaxEntry(i);
// Pivoting
if (i != maxIdex) {
pivot(i, maxIdex);
}
// Eliminate
eliminate(i);
}
};
let solve = function(B) {
let dim = self.A.length;
let P = self.P;
let L = self.L;
let U = self.U;
let PB = MatrixUtil.Multiply(P, B);
let i, j;
//LUX = PB
//UX = Y ==> LY = PB
let Y = [];
for (i = 0; i < dim; i++) {
let l = L[i];
let temp = 0;
for (j = 0; j < i; j++) {
temp = temp + l[j] * Y[j][0];
}
Y.push([PB[i][0] - temp]);
}
// UX = Y
let X = [];
for (i = dim - 1; i >= 0; i--) {
let u = U[i];
let start = i + 1;
let temp = 0;
for (j = start; j < dim; j++) {
temp = temp + u[j] * X[j - start];
}
X.unshift([(Y[i][0] - temp)/u[i]]);
}
return X;
};
// Public methods
self.SetA = setA;
self.PLU = PLU;
self.Solve = solve;
};
这个构造函数公开了三个方法。
- “SetA()”——它允许您设置 A 矩阵。它还初始化 P、L 和 U 矩阵;
- “PLU()”——它对 A 矩阵执行 LU 分解;
- “Solve()”——它接受一个列向量 B 并求解方程 AX = B。您需要确保在调用“PLU()”方法之后调用它。
因为我们使用的是 Javascript,所以在调用“SetA()”方法设置的 A 矩阵的“PLU()”方法后,您可以通过 LU 对象的实例访问 P、L 和 U 矩阵。
示例
示例“index.html”
为了试用我的 LU 分解实现,我创建了一个小型示例程序。
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
<title>lu-decomposition-example</title>
<link rel="stylesheet" type="text/css" href="styles/app.css">
<script type="text/javascript" src="script/MatrixUtil.js"></script>
<script type="text/javascript" src="script/lu-decomposition.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/react/15.6.1/react.min.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/react/15.6.1/react-dom.min.js"></script>
<script type="text/javascript">
// The example equition AX = B
let A = function() {
let A = [];
A.push([2,1,1,0]);
A.push([4,3,3,1]);
A.push([8,7,9,5]);
A.push([6,7,9,8]);
return A;
}();
let B = function() {
return [[5], [8], [1], [7]];
}();
// Matrix DOM
let React_Matrix = React.createClass({
render: function() {
let M = MatrixUtil.Round(this.props.M, 2);
return React.DOM.table({className: 'matrix bb'},
M.map(function(row, i) {
return (React.DOM.tr({key: i},
row.map(function(e, j) {
let p = {key: j};
let s = {style: {'padding-right': '1px',
visibility: (e < 0)? 'visible' : 'hidden'}};
return React.DOM.td(p,
React.DOM.span(s, '-'),
React.DOM.span(null, Math.abs(e)));
})
));
})
);
}
});
let React_Main = React.createClass({
getInitialState: function() {
let lu = new LU().SetA(A);
return { lu: lu, A: lu.A, B: B, P: lu.P, L: lu.L, U: lu.U };
},
LUandSolve: function() {
let state = this.state;
let lu = this.state.lu;
lu.PLU();
let X = lu.Solve(state.B);
let R = MatrixUtil.Subtract(B, MatrixUtil.Multiply(state.A, X));
let RT = MatrixUtil.Transpose(R);
let Residual = MatrixUtil.Multiply(RT, R)[0][0];
this.setState({ P: lu.P, L: lu.L, U: lu.U, X: X, Residual: Residual});
},
Reset: function() {
let lu = this.state.lu;
lu.SetA(A);
this.setState({ P: lu.P, L: lu.L, U: lu.U, X: null, Residual: null });
},
render: function() {
let state = this.state;
let e = [];
e.push(React.DOM.div(null,
React.DOM.button({ onClick: this.LUandSolve, className: 'btn' },
'LU & Solve Equition'),
React.DOM.button({ onClick: this.Reset, className: 'btn' }, 'Reset')));
let X = state.X;
let Residual = state.Residual;
e.push(React.DOM.div({className: 'y-center'},
React.DOM.div(null, React.DOM.div({className: 'semi-bold'}, 'A'),
React.createElement(React_Matrix, {M: state.A})),
(X != null)? React.DOM.div(null, React.DOM.div({className: 'semi-bold'},
'X'), React.createElement(React_Matrix, {M: state.X}))
: React.DOM.span({className: 'semi-bold',
style: {padding: '0px 5px'}}, 'X'),
React.DOM.span({style: {padding: '0px 5px'}}, '='),
React.DOM.div(null, React.DOM.div({className: 'semi-bold'}, 'B'),
React.createElement(React_Matrix, {M: state.B}))));
e.push(React.DOM.div(null, (Residual == null)? null
:React.DOM.span({style: {padding: '0px 5px'}},
'Residual = ' + Residual)
));
e.push(React.DOM.div({className: 'y-center'},
React.DOM.div(null, React.DOM.div({className: 'semi-bold'}, 'P'),
React.createElement(React_Matrix, {M: state.P})),
React.DOM.div(null, React.DOM.div({className: 'semi-bold'}, 'A'),
React.createElement(React_Matrix, {M: state.A})),
React.DOM.span({style: {padding: '0px 5px'}}, '='),
React.DOM.div(null, React.DOM.div({className: 'semi-bold'}, 'L'),
React.createElement(React_Matrix, {M: state.L})),
React.DOM.div(null, React.DOM.div({className: 'semi-bold'}, 'U'),
React.createElement(React_Matrix, {M: state.U}))));
return React.DOM.div(null, e);
}
});
window.onload = function() {
ReactDOM.render(React.createElement(React_Main),
document.getElementById('example'));
};
</script>
</head>
<body>
<div id="example"></div>
</body>
</html>
这个示例使用 React 来显示矩阵。如果您不熟悉 React,可以查看我之前的笔记或访问官方 React 网页。
- A 和 B 矩阵在程序开头初始化;
- 网页上添加了两个按钮。“LU & 求解方程”按钮将执行 LU 分解并求解方程 AX = B。“重置”按钮将重置结果,让您可以再次尝试;
- 所有结果,包括 P、L、U 和方程的解,都通过浏览器中的 React 显示。
运行示例
如果您使用的不是非常老的浏览器,您应该能够加载示例并进行尝试。由于网页引用了 React 库的 CDN,因此您的计算机需要有互联网连接。

加载示例时,所有矩阵都已初始化。如果您点击“LU & 求解方程”,则会对 A 矩阵执行 LU 分解并求解 AX = B 方程。

您可以看到 X 的解以及方程解的残差。您还可以点击“重置”按钮清除结果并再次尝试。
关注点
- 这是一篇关于 Javascript 中 LU 分解的说明;
- 求解线性联立方程组的方法是一个非常重要的课题。LU 分解是数学家赐予我们的一个极好的工具。显然,这篇说明并不是故事的终结。我们仍然有许多问题,例如如何处理奇异矩阵以及如何利用矩阵的稀疏性。但这些问题超出了这篇说明的范围;
- 希望您喜欢我的博文,并希望这篇笔记能以某种方式帮助您。
历史
首次修订 - 2017 年 8 月 26 日。
