统计学 R FORTAN 文本机器学习 C 中间开发

使用 k-means 进行中间数据聚类

Andy Allinger

5.00/5 (35投票s)

2017年8月28日

公共领域

54分钟阅读

57358

1232

为k-means添加缺失数据、混合数据和选择聚类数量的功能

下载源代码 - 181.8 KB

背景：聚类概述

引言。 K-means 是最常用的数据聚类方法，因为它简单、快速，并且通常能产生良好的结果。该算法在两个主要步骤之间交替进行

将每个点分配到其最近的中心
将每个中心设为其点的平均值

该方法的一个吸引力在于其易于泛化的程度。一个简单的实现 [*] 将“点”定义为实数向量，“中心”定义为算术平均值，“最近”定义为根据勾股定理计算的距离。更一般地，“点”可以是各种类型的数据，“中心”可以是各种类型的平均值，“最近”距离可以泛化为不相似度函数，其中有无数种选择。

数据聚类是一项基本操作：它将相似的事物聚集在一起，并将不同的事物分开。这是一项强大的技术，适用于各种各样的问题。在之前的 CodeProject 文章中，Samir Kunwar 讨论了它在文本聚类中的应用，Rodrigo Costa Camargos 探索了凝聚聚类，Arthur V. Ratz 在推荐系统中应用了 k-means。本项目提供了一个 k-means 实现，可以应用于混乱的真实世界数据，并且效率也很高。

数据类型

更详细的讨论可以在 [Kaufman & Rousseeuw, 1990] 的“数据类型及其处理方法”一章中找到。

连续型。 这些是实数向量。假设您有一个天气监测站，记录温度、气压和湿度。每次观测都可以表示为一个具有三个分量 (T, p, h) 的向量。这些测量值中的每一个都是连续变量。它们不需要具有相同的测量单位。

类别型。 相反，假设数据只能取某些特定的值。例如，您可能不测量温度，而是记录天气是晴朗、下雨还是下雪。心脏杂音可能存在或不存在。问题可能回答“是”或“否”。动物可能是雄性或雌性。

二分型。 当一个变量的两个可能值中的一个比另一个更有信息量时，就会出现一种特殊情况。假设气象站记录龙卷风是否存在。由于龙卷风只在特定条件下发生，有龙卷风的日子是相似的，而没有龙卷风的日子可能不相似。有羽毛的动物有一些共同点，而没有羽毛的动物可能没有任何共同点。二分型数据也称为“二元不对称”。

有序型。 假设温度记录为热、暖、凉或冷，而不是数值。在赛跑者中，可能知道他们是第一名、第二名还是第三名，但可能不知道他们的完赛时间。有序变量类似于类别变量，但其值可以按特定顺序排列。

时间序列。 假设您的气象监测站只测量温度，但您每年每小时都进行一次测量。那么全年的记录都可以被视为一个观测值，并且可以与其他气象站的年度记录进行比较。（本程序不处理时间序列。）

直方图。 也许对象不是单一的测量值，而是一系列形成统计分布的测量值。合适的直方图比较方法包括特殊的距离度量，例如“Earth Mover's distance”（推土机距离）。（本程序不处理直方图。）

多媒体。 也许您的数据是音频、图像或视频。这个问题会变得很困难，但已经发明了一些方法来比较它们的不相似性。[Deza & Deza, 2012] （本程序不处理多媒体。）

不相似度类型

不相似度函数是数据聚类的核心。它量化了差异。多年来，已经设计了各种各样的不相似度函数。有些有坚实的理论基础，有些则没有。[Podani, 2000] [Sung‐Hyuk, 2007] [Boriah, Chandola & Kumar, 2008] [Deza & Deza, 2012]

一个椭球形数据云最重要的是欧几里得距离，这是几何学中教授的那种，由勾股定理给出

$ d(X,Y) = \sqrt{ \sum {(x_i - y_i)}^2} $

它之所以重要，是因为许多现实世界中的概率分布呈椭球形。欧几里得距离与球形分布概率的负对数成正比。因此，如果输入数据经过适当缩放，使得变量具有相似的方差，并且输入变量大部分是独立的，那么欧几里得距离就近似于一个对象属于某个组的不可能性。

曼哈顿不相似度。 一些作者 [Kaufman & Rousseeuw, 1990] 建议不使用勾股定理，而是根据 L1 度量（有时称为出租车、城市街区、曼哈顿）计算距离

$d(X,Y) = \sum\left|X_i - Y_i\right|$

曼哈顿度量对极端值（可能是错误的）不那么敏感，因为差值没有平方。然而，它对应于平行四边形分布，这在自然界中可能不存在。[*] 平行四边形数据云的样子

相关性。 假设数据是若干年河流流量的时间序列。计算标准相关性将显示一条河流的流量与另一条河流的流量之间是否存在关系，这与河流的平均大小无关。

$ r = \frac{\sum xy}{\sqrt{(\sum x^2)(\sum y^2)}}$ 其中 x 已通过减去 X 的平均值进行中心化：$x_i = X_i - \bar{X}$ 并且：$y_i = Y_i - \bar{Y}$

相关性是一种相似度度量。通过取反余弦，它可以转换为不相似度度量。[*]

$d(X,Y) = \arccos(r)$

交叉熵。 假设数据是离散变量的某些观测值。通常的例子是一些豆子罐，每个罐子中红豆、黑豆和白豆的比例不同。然后，样本与特定罐子之间的交叉熵

$ H(S,M) = -\sum P_s \log(P_m) $

是样本来自该罐子的负对数概率。这里，S 代表样本，M 代表模型。请注意，这种不相似度不是对称的

$ H(S,M) \neq H(M,S) $

缺失数据的不相似度函数。 处理缺失数据的最简单方法是通过非缺失数据的简单线性外插来补偿缺失值。John Gower 提出了一种相似度系数，该系数已被修改为不相似度函数 [Gower, 1971][Kaufman & Rousseeuw, 1990]

$ d(X,Y) = \frac{\sum \delta(x,y) f(x,y)}{\sum \delta(x,y)} $

其中 δ(x, y) 是一个指示函数，当对象 X 和 Y 对于某个变量都存在数据时，其值为 1，否则为 0。函数 f(x, y) 取决于数据类型。连续型和有序型属性必须缩放到 0 到 1 的范围，然后 f(x, y) 是 x-y 的绝对值。对于类别型数据，如果值匹配，f(x, y) 为 0，如果不匹配，则为 1。二分型属性会得到特殊处理。因为 {缺失, 缺失} 对被认为完全没有信息量，所以这种情况被视为缺失值。

Gower 的不相似度似乎是最常用的，但不是唯一的选择。1970 年，Burnaby 提出了一种相似度度量，该度量应用了对独立属性和稀有值给予更多重要性的因子。[Carranza, Feoli & Ganis, 1998] 它可以以与 Gower 相同的方式处理缺失数据。

处理缺失数据的另一种方法是用该属性的平均值替换它，正如 [Anderson, 1971] 中提出的。还有一种可能性是，当缺失值时使用平均不相似度。

其他变体也是可能的。差值可以进行平方，而不是取绝对值。这会得到一个类似于勾股定理的公式 [Podani, 2000]。通常 [*] 没有必要将连续属性缩放到 0...1，并且可以引入其他加权方案，例如 [Huang, 1997]。

最小化平方距离之和。 聚类的目标是将数据分区，使得彼此靠近的对象位于同一组中。为了评估这一目标达到的程度，计算残差误差，定义为每个点到其分配的中心的平方距离之和。有时错误地声称简单的 k-means 方法找到了误差的局部最小值。[*] 这没有考虑到改变点的分配对中心的影响。为了找到平方误差的局部最小值，不相似度函数必须是平方欧几里得距离，如果点属于中心，则应用修正因子 $\frac{N}{N-1}$，如果点不属于中心，则应用修正因子 $\frac{N}{N+1}$。[Hartigan & Wong, 1979]

平均值类型

均值。 这是最熟悉的平均值类型。 $ \overline{x} = \frac{\sum x_i}{N} $ 均值对极端值敏感。它不适用于类别属性。

中位数。 中位数是排序列表中中间的值。它也不适用于类别属性。

众数。 众数是数据集中最常见的值。它适用于类别属性。如果有许多可能的值，那么数据集中的少数对象可能实际上具有该值。

中心点 (Medoid)。 中心点是数据集中与其他所有对象总不相似度最低的对象。只要定义了不相似度，它就可以用于任何类型的数据。它具有与众数相同的缺点。由于不可能有小数类，因此它无法代表多样化的集合。

聚类之间的不相似度

如果两个聚类可以由它们的均值或中位数表示，那么它们之间的距离很容易找到。类别变量的情况不太清楚。众数或中心点可能无法准确表示聚类。如果我们取来自每个聚类的对象对，并计算平均不相似度，正如 [Kaufman & Rousseeuw, 1990] 所做的那样，可能会出现一些奇怪的现象。考虑两群动物，每群一半是雄性，一半是雌性。那么这两群之间的平均不相似度是 50%。现在考虑两群动物，一群一半雄性一半雌性，另一群全是雄性。这两群之间的平均不相似度仍然是 50%！

确定聚类数量

k-means 的一个显著弱点是它需要预先指定聚类数量 k。通常的做法是为几个 k 值运行 k-means，然后检查结果。残差误差可以测量为每个点到其中心的总距离。随着 k 的增加，这个残差会减小。直觉是，当达到正确的 k 值时，残差会显著减少，并且更多的额外聚类不会带来显着的改进。这种通用方法有时被称为肘部法则 (Elbow Method)。多年来，已经提出了许多这种思想的变体。Milligan & Cooper 在 1985 年对选择聚类数量的 30 种方法进行了调查。为 GNU "R" 统计语言发布了一个软件包 [Charrad et al., 2014]，实现了 30 种方法，其中一些是相同的。目前似乎没有关于肘部法则最佳变体的共识。

另一种方法是猜测 k 的初始值，然后运行 k-means 的一个变体，该变体允许更改聚类数量。[Ball & Hall, 1965] [Pelleg & Moore, 2000] [Kulis & Jordan, 2012] 这种方法的缺点是必须指定更多参数来决定何时应拆分聚类，何时应合并聚类。

有人建议 k-means 可以运行几次，使用不同的 k 值，并选择一个产生最一致结果的 k 值。这种方法可能非常糟糕，如 [Ben-David, von Luxburg, & Pál, 2005] 所示。

聚类数量取决于变量的权重。要理解这一点，假设最初有六个聚类。降低水平方向的重要性会产生两个聚类。降低垂直方向的重要性会产生三个聚类。

blue dots in 6 groups. The groups are arranged on a 2 by 3 grid. blue dots in two, long rectangles, arranged end to end blue dots in three long, skinny rectangles, arranged end to end.

历史

这些信息大部分来自 [Bock, 2008] 的综述文章.

1950 Dalenius 提出了一种划分一维数据集的方法。
1953 Thorndike 非正式地描述了一种使用平均距离的聚类方法。[Thorndike, 1953]
1956 Steinhaus 提出了一种用于连续情况的 k-means 算法。
1957 Lloyd 提出了一种一维 k-means 算法；他的论文直到 1982 年才被广泛发表。
1965 Forgy 在一次讲座和摘要中提出了基本的 k-means 算法。
1965 Ball & Hall 发表了一种更复杂的算法，其中提供了合并和拆分聚类的功能。[Ball & Hall, 1965]

CLUELA 包

CLUELA 是 CLUstering with ELAborations（带详细说明的聚类）的缩写。它扩展了基本的 k-means 算法，以处理缺失数据、混合数据和选择聚类数量的问题。它将原始代码和遗留代码整合到纯粹、诚实的 FORTRAN 中，并提供完整的 C 翻译。它旨在提高应用程序的使用效率，并且编写清晰，以便其他程序员可以对其进行修改。

数学计算采用单精度。在统计学中，问题不在于数字是否足够精确，而在于它们是否有意义。

缺失数据支持

我们需要一种方法来表示数据是存在还是缺失。可以将某个特殊值（“哨兵值”）留作缺失数据，但这不可避免地会导致冲突。为了真正充分地指示存在什么，需要另一个数组。（类似于 C Clustering Library. [de Hoon, Imoto, & Miyano, 2010] 中的实现）整数矩阵 NX 的每个元素，如果数据矩阵 X 中对应的元素存在，则应设置为 1，如果缺失，则设置为 0。

不相似度函数是 Gower 不相似度，由 Kaufman & Rousseeuw 修改，并扩展以支持每个变量的重要性权重 [*]，并泛化以支持曼哈顿和欧几里得度量

$ d(X,Y) = \left(\frac{\sum \delta(x_j,y_j) w_j \left|x_j - y_j\right|^L}{\sum \delta(x_j,y_j) w_j} \right)^{\frac{1}{L}} $

其中 δ(x,y) 是一个指示函数，当 X 和 Y 都存在数据时其值为 1，否则为 0。
L 分别为 1 或 2，代表曼哈顿或欧几里得度量。

如果设置了 ROBUST 选项，则使用曼哈顿度量，否则使用欧几里得度量。ROBUST 选项还将中心计算为中位数而不是均值，因此 CLUELA 实现的是k-中位数算法。

混合数据

当前实现的不相似度函数仅接受连续型数据。这样做不是因为实现 Gower 不相似度有任何困难，而是为了使平均值始终能够清晰定义。CLUELA 实现的是 k-means 而不是 Kaufman & Rousseeuw 的 k-medoids 算法，因为中心点可能无法准确代表聚类。

为了处理类别型数据，包含了子例程 RSCODE 来将类别变量重新编码为几个连续变量。最明显也是最常见的做法是使用虚拟编码 (dummy coding)。一个具有 c 个可能值的类别变量被重写为 c 个连续变量。对应于对象类别的连续变量设置为 1，其余连续变量设置为 0。虚拟编码包含冗余信息，因为如果已知 c - 1 个虚拟编码值，则最后一个值就完全确定了。这稍微效率低下，并且如果我们想计算协方差矩阵（例如，运行 PCA）时可能会导致数值问题。因此，最好用 c - 1 个连续变量来表示一个取 c 个可能值的类别变量。一个正四面体，一个有四个顶点和四个面的三维形状。每个面都是一个三角形。 正单纯形 (regular simplex) 是一个 N 维的正则多面体推广。[McCane & Albert, 2007] 一个具有 c 个顶点的正单纯形位于 c - 1 维空间中。例如，具有四个顶点的正单纯形是四面体，它是一个普通的三维对象。[*] 如果设置了 ROBUST 选项，则数据被嵌入到曼哈顿单纯形中，使得顶点根据曼哈顿度量相距 1，否则数据被嵌入到普通的欧几里得空间中。由于重编码增加了变量的数量，为了保持不相似度与简单匹配类别变量相同，必须将重要性权重按比例缩小。然后需要相应地按比例放大重编码后的数据。

子例程 RSCODE 需要输入形式为小的连续整数的 REAL 近似值，即 1.0、2.0、3.0……要研究的原始数据将以一种不那么方便的格式呈现。提供了两个子例程来进行这种转换：JSCODE 将任意整数重新编码为小的连续整数，IREID 将 CHARACTER 数据重新编码为小的连续整数。

有序型数据可以按原样保留，并作为连续型数据处理。或者，可能更倾向于认为稀有、极值比常见值更不相似。子例程 ORDNAL 将排名替换为其分位数，缩放到 0 到 1，这样“Cold”和“Cool”之间的差异在“Cold”在数据集中出现次数很少时会更大。

二分型数据不能用虚拟编码或正单纯形表示。有必要使用下面描述的 MDS 进行嵌入。[*] 二分型变量的使用仅在“大豆问题”中演示。

选择聚类数量

用户必须指定 KMIN（最少可接受的聚类数），KMAX（最多可接受的聚类数），以及 K（默认聚类数）。该子例程运行 k 从 KMIN-1 到 KMAX 的 k-means，并记录 k 从 KMIN 到 KMAX 时残差的改善情况。在提出的确定聚类数量的许多方法中，**gap statistic**（差距统计量）受到好评，但计算成本很高。Pham, Dimov & Nguyen 在 [2005] 中开发了一种快速近似方法。选择产生该统计量最小值的 k 值，除非未达到临界值，在这种情况下，将接受默认的聚类数量。

其他特性

初始中心通过通常的 k-means++ 方法选择。对于每个 k 值，k-means 使用不同的初始中心运行十次。保留残差最小的结果。

设置 SOSDO 选项可启用 $\frac{N}{N-1}$ 或 $\frac{N}{N+1}$ 的修正因子，以找到平方距离目标和的局部最小值。此选项与 ROBUST 选项冲突。它还与构建二叉树（见下文）冲突，因此不是默认选项。

外部验证。 有时，您可能想将 k-means 生成的分区与另一个分区进行比较。例如，您可能希望在一个具有已知答案的问题上测试聚类算法。为此提供了两个子例程。ARIND 计算调整后的 Rand 指数 (ARI)，这是一个准确性度量，最大值为 1。当聚类与外部标准的一致性达到随机预期时，它为 0。如果一致性甚至比随机预期差，它可以取负值。VINFO 计算信息变异性。[Meilă, 2002] 它衡量聚类与外部标准之间的距离，因此值越小表示一致性越好。其最小值为 0；最大值取决于问题的大小。

多维缩放：老板喜欢图表

如果您必须传达您的分析结果，您将需要一些视觉辅助工具，以便听众有东西可看。要可视化多变量数据，必须先将其投影到二维。这可以通过多维缩放 (MDS) [Laub, 2004]、奇异值分解或主成分分析来完成。子例程 MDS 和 PCA 已包含在内。

多维缩放接受一个由*平方*不相似度组成的矩阵，并给出欧几里得空间中点的坐标，这些点的距离恰到好处。该技术通用且强大。它曾被 [Tobler & Wineburg, 1971] 著名地用于仅根据它们在同一粘土板上的提及来定位安纳托利亚的古代城市。将双中心化公式应用于矩阵

$ C_{ij} = (-\frac{1}{2}) \left((A_{ij} -\frac{1}{N}\sum_{k=1}^NA_{ik} -\frac{1}{N}\sum_{k=1}^N A_{kj} + \frac{1}{N^2}\sum_{k=1}^N\sum_{l=1}^N A_{kl}\right) $

对矩阵进行因子分解，并将每个特征向量乘以其对应特征值的平方根。

CLUELA 中实现的 MDS 不那么通用，它绑定到 Gower 不相似度函数。因此，它支持混合和缺失数据，并且可以用于填充缺失值，作为那些没有缺失数据支持的例程（如 KMNS 和 NEUGAS）的预处理步骤。如果存在任何二分型数据，也必须使用 MDS，因为 CLUELA 无法直接处理它们。

PCA 不支持缺失数据，但它可能比 MDS 快得多。它只需要对 PxP 协方差矩阵进行因子分解，而不是通常更大的 NxN 不相似度矩阵。对于 PCA，我们必须首先计算协方差矩阵

$ \sigma_{jk} = \frac{\Sigma((x_{ji} - \bar{x_j})(x_{ki} - \bar{x_k}))}{N - 1} $

找到特征值和特征向量，对协方差矩阵进行因子分解 $V \Lambda V^T$。投影是 $R = X^T V$，只使用对应于 M 个最大特征值的 V 的列。请注意，R 相对于 X 是转置的。

选项是使用协方差矩阵或喜剧演员矩阵。[Falk, 1997] 喜剧演员

$ com(X,Y) = med{(X - med(X))(Y - med(Y))} $

是中位数绝对偏差的推广。它是协方差的一种高度稳健的替代方法，易于计算。

效率改进

k-means 通常被描述为快速，或者至少比其他一些聚类算法快。基本 k-means 的计算成本是 NPKi 次运算，其中 N 是对象数量，P 是变量数量，K 是聚类数量，i 是收敛所需的迭代次数。有可能修改算法使其比这更快，并且这些效率改进不会损失准确性。

k-means 的瓶颈步骤是计算每个点到每个中心的距离。可以通过将中心放入二叉树数据结构来在不测量到每个中心距离的情况下找到点到最近中心的距离。[Chávez, Novarro, & Marroquín, 1999] CLUELA 使用广义超平面树。任何具有每个数据点之间不相似度的数据集都可以通过选择两个对象，并将剩余对象分配给一个分区（根据它们离第一个还是第二个更近）来分割。如果数据和不相似度函数满足度量空间的条件，则可以使用三角不等式来有效地搜索树以查找最近邻。（参见附录）度量空间有四个要求

不相似度不为负
当且仅当对象相同时，不相似度为零
对象之间的不相似度是对称的
三角不等式：A 到 B 的不相似度加上 B 到 C 的不相似度必须大于或等于 A 到 C 的不相似度。

曼哈顿不相似度和欧几里得不相似度是度量。其他一些当前关注的不相似度函数不是度量。特别是，*平方*欧几里得距离*不是*度量。当存在缺失数据时，Gower 不相似度不是度量。最小化平方距离之和的不相似度函数不是度量。当 K 很大而 P 很小时，广义超平面树最有价值。CLUELA 在满足度量空间条件时构建广义超平面树。否则，它将穷举比较每个点与每个中心。

在度量空间中，如果一个点到其最近中心的距离小于或等于该中心到任何其他中心的距离的一半，则该点不可能属于任何其他聚类。在这种情况下，无需计算任何距离。[Elkan, 2003] （参见附录。）

Hartigan & Wong 引入了“活动点”和“活动中心”的概念，以消除不必要的距离计算。[Hartigan & Wong, 1979] 如果在上一次迭代中向中心添加或从中删除了任何点，则该中心处于活动集中。如果一个点到其最近中心的距离自上次迭代以来增加了，则该点处于活动集中。对于每个点，活动中心可能变得更近，因此每个点必须与所有活动中心进行比较。对于活动点，其当前中心距离更远，因此该点必须与所有死活中心进行比较。如果点及其中心均未处于各自的活动集中，则不可能发生变化，并且可以跳过计算。此推理不依赖于度量空间的属性。CLUELA 始终利用活动集。

对于某些类型的数据和不相似度函数，k-means 可能会陷入循环而永远无法收敛。分配数组 Z 被哈希，并且哈希存储在环形缓冲区中。在每次迭代中，将当前哈希与前一个哈希值进行比较，以检测算法是否陷入循环。如果陷入循环，它将无错误地退出。（CLUELA 中的标量数据可能无法陷入循环。为了程序员修改子例程以处理行为不那么好的数据，保留了循环检测功能。）

要计算每个聚类的中位数，必须将数据重新打包到工作数组中。为避免进行 K 次遍历数据矩阵来填充工作数组，对分配数组使用被动排序。然后，就可以在不引用其他对象的情况下访问每个聚类的点。由于分配数组是小整数，因此可以使用不稳定的基数排序对其进行特别高效的排序，计算成本为 N log(K)。

通过使用二叉树，分配步骤的计算成本从 NPK 降低到可能低至 NP log(K)，具体取决于树的有效性。通过对数据进行排序，计算中心的成本是 NP（数据矩阵的大小）；或者 N log(K)（排序的成本）。然后，瓶颈步骤是 k-means++ 初始化。另一种初始化方法是使用超平面分区。这与将数据放入广义超平面树非常相似，只是忘记了树结构的所有细节。使用这种快速初始化，整个聚类过程的复杂度低于 O(NPK)。

关于翻译

原始代码全部是用“遗留”FORTRAN 编写的——也就是说，任何 f2c 都能接受的。这是标准的 FORTRAN 77，带有一些扩展。f2c 翻译了它，然后对其进行了编辑，以删除对 libf2c 的依赖，并使矩阵双下标化。双下标化可能运行更快，也可能不快，但更容易阅读。没有 random.c 或 machine.c，因为机器常数和随机数是标准 C99 的一部分。同样，没有 array.f，因为在 FORTRAN 中声明矩阵没有什么特别之处。参数列表通常不同。FORTRAN 中的一些参数在 C 中是多余的，反之亦然。没有头文件。

Using the Code

大多数聚类问题的解决方案都需要预处理阶段、聚类本身，然后进行一些额外的后处理。

子例程 CLUELA 仅接受实数向量作为输入。文本标签或整数形式的数据可以通过调用 IREID 或 JSCODE 分别转换为小的连续整数。有序型数据可以选择使用 ORDNAL 进行重新缩放。如果您决定标准化部分或全部变量，均值和标准差可以使用 AVEDEV 计算，或者中位数和中位数绝对偏差可以使用 MEDMAD 计算。范围可以使用 LEAGRE 找到。标准化会缩小方差较大的变量，因此可能适得其反。如果变量单位不同，则需要某种转换。缩放到 0 到 1 的范围可能是更好的选择

$ x'_i = \frac{x_i - x_{min}}{x_{max} - x_{min}} $

为了进行比较，分布中包含了经典的 k-means 实现 KMNS 和替代的神经网络聚类算法 NEUGAS。子例程 CLUSTE 是 CLUELA 的一个变体，它跳过重复项并使用快速初始化以获得更快的理论效率。

在后处理阶段，可以调用 MDS 或 PCA 将数据投影到较低维度，以便进行图形化。MDS 也可以在预处理阶段使用。它接受二分型数据，而 CLUELA 和 CLUSTE 不接受。它还会填充缺失数据，以便可以使用 KMNS 或 NEUGAS。使用 WCSVSP 将 2D 结果写入电子表格。

应用程序员可能感兴趣的其他子例程包括

MEDIAN：实数向量的中位数，作者：Alan Miller
SAFDIV：检查除法是否会溢出，基于 Julio 的程序
ALMEQ：检查两个实数是否近似相等
SHUFFL：生成 1...N 整数的随机排列
OSIMAN：通过模拟退火优化一组参数
DINIT：根据 k-means++ 方法选择初始聚类中心
HCLUST：通过超平面分区选择初始点分配
KCLUST：k-means 或 k-medians 聚类，支持缺失数据，并可以插入或删除聚类

有关这些子例程的调用序列，请参阅源代码。所有重要的子例程都有说明如何使用它们的前言。

示例问题

大豆问题演示了如何调用 CLUELA 对混合和缺失数据以及二分型变量进行聚类。使用 R 中的 daisy 和 pam 检查结果。
葡萄酒问题表明，聚类数量取决于变量的重要性权重。
信用审批问题显示了如何直接调用 KCLUST。
圆形问题显示，对于大量聚类和少量维度，CLUSTE 比 KMNS 更快。
马科疾病问题演示了一种优化重要性权重的方法。它还展示了如何调用 NEUGAS。
投票问题是稳健主成分与标准主成分差异很大的情况。
森林火灾问题考虑了循环变量的情况，并展示了如何使用虚数嵌入分量。

这些问题中的大多数来自加州大学欧文分校机器学习存储库。[Lichman, 1987] 大豆、葡萄酒、信用、投票最初被视为分类问题。已知的类别可以用作聚类结果的外部验证度量。

训练集和测试集已合并为soybean.both 和 horse-colic.both。这是允许的，因为聚类不进行训练。所有先验假设都已内置到不相似度函数和重要性权重中。

葡萄酒问题的重要性权重来自优化谱聚类残差，并且不涉及类别标签的使用。圆形、信用、投票和火灾问题使用相等的权重。马科疾病问题权重通过模拟退火优化确定。对于大豆数据，权重是通过某种线性变换获得的，我不记得它是否涉及查看类别标签，所以请不要太认真对待它们。

所有数据集都包含在发行版中。

大豆问题

一些病株患有 19 种疾病，表现为 35 种症状，这些症状是连续型、类别型和有序型变量的混合。症状和疾病是由人类专家识别的，这应该让我们产生怀疑，因为这不是双盲实验。农民的诊断可能影响了他对症状的描述。大量数据缺失。十二个变量是二元的，在不到 25% 的实例中值为“存在”。这些可以合理地作为二分型变量来处理。我们将比较将这些变量视为类别型或二分型变量的结果，然后通过在 GNU R 中调用 daisy 和 pam 重新运行问题来检查这些结果。

合并训练集和测试集后，对象数量 N 为 683。类别数量 G 为 19。考虑可能的聚类数量从 KMIN=1 到 KMAX=50。原始变量数量 O 为 35。其中许多变量需要重新编码。硬编码数组 CAT(O) 给出了每个输入变量的类别数。对于连续型和有序型变量，写零。对于二分型变量，写*一*。将 CATMAX 设置为 CAT 中的最大值。每个类别变量都需要用比类别数少一的连续变量数量进行重新编码。输入到聚类例程的数据矩阵是 X(P,N)。要找到 P，从 O 开始，并为每个类别变量加上 CAT(H)-2。子例程*不*自动执行此操作；它必须硬编码在主程序中。分析师检查数据并思考问题非常重要。

研究输入，我们发现 P=54。soybean.both 中的属性值对于可用数据是整数 0, 1, 2...，对于缺失数据是“?”。RSCODE 要求类别从 1.0 开始编号。对于可用数据，X 设置为 1.0 + 输入，NX 设置为 1。对于缺失数据，X 设置为 XBOGUS，NX 设置为 0。

X 的前 O 行用输入填充。连续型和有序型变量缩放到 0 到 1，以匹配 daisy 中的处理。调用 MDS，将二分型变量视为类别型，并获得嵌入矩阵 VC。然后将二分型变量从 {1.0, 2.0} 更改为 {0.0, 1.0}，因为按照惯例，这是二分型 {缺失, 存在} 的编码。调用 MDS，识别二分型变量，并获得嵌入矩阵 VD。

调用 RSCODE 使用正单纯形的顶点来重新编码类别变量。这会占用更多内存。RSCODE 从最后一行开始向后工作，将数据移动到数组的末尾，返回 X(P,N) 的所有连续数据。类别标签以文本字符串形式给出；必须使用调用 IREID 将它们转换为整数 1, 2, 3...。设置默认 K = 20，我们终于可以调用主子例程了。返回后，将结果与类别标签进行比较，并将投影数据写入 soy_clusters.csv 和 soy_classes.csv。Pham, et al. [2005] 的 F 统计量以数组 F() 的形式返回给每个可能的聚类数量 KMIN...KMAX。小的 F 值应该表示一个好的聚类数量。

接下来，通过调用 CLUELA 并使用嵌入矩阵 VD 替换 X 来重复该过程，使用二分型变量。像以前一样打印输出。作为检查，再次对重编码的 X 调用 MDS，将所有变量视为连续型，获得嵌入矩阵 VR。比较 VR 和 VC 可确保 RSCODE 返回的坐标代表的对象之间的不相似度与原始数据相同。

运行程序将打印到终端

cluela returns #0, made 2 clusters
Returned residual:   1.566e+04
Adjusted Rand Index: 0.154
Variation of Information:  3.025
cluela returns #0, made 2 clusters
Returned residual:       124.6
Adjusted Rand Index: 0.164
Variation of Information:  3.004
Greatest difference between original and recoded embeddings: 5.60e-04
program complete

调整后的 Rand 指数 (ARI) 的此值表明聚类比猜测好 15%。检查聚类结果的图，我们看到 CLUELA 产生了合理的两个聚类分区。MDS 或 PCA 嵌入轴的方向是任意的。翻转垂直方向，类别型和二分型之间的差异很小。

类别分布方式更加复杂

F 值的图显示了对两个聚类的强烈偏好，而在 19 处没有。

这是我们对大豆数据的方法或对 F 统计量产生怀疑的理由。我们将在下一个问题中看到，F 统计量有时有帮助，但并非总是如此。

让我们将这些结果与 GNU R 中的解决方案进行比较。以交互模式启动 R，更改目录，并加载 cluster 包

R
setwd('~/cluela')
library(cluster)

将文件读入数据框 x，将变量 3、4、6、8 和 10 设置为有序型，并检查输入

x <- read.table('soybean.both', header=FALSE, sep=",", na.strings="?", 
colClasses=list("character", "numeric", "factor", "factor", "factor", 
"factor", "factor", "factor", "factor", "factor", "factor", "factor", 
"factor", "factor", "factor", "factor", "factor", "factor", "factor", 
"factor", "factor", "factor", "factor", "factor", "factor", "factor", 
"factor", "factor", "factor", "factor", "factor", "factor", "factor", 
"factor", "factor", "factor"))[2:36]
x[3] <- ordered(x[,3])
x[4] <- ordered(x[,4])
x[6] <- ordered(x[,6])
x[8] <- ordered(x[,8])
x[10] <- ordered(x[,10]) 
str(x)

这将产生

'data.frame':    683 obs. of  35 variables:
 $ V2 : num  6 4 3 3 6 5 5 4 6 4 ...
 $ V3 : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 1 ...
 $ V4 : Ord.factor w/ 3 levels "0"<"1"<"2": 3 3 3 3 3 3 3 3 3 3 ...
...

设置权重，调用 daisy 计算每个对象之间的不相似度矩阵。检查不相似度

w <- c(2.742, 1.944, 6.565, 2.532, 2.200, 2.227, 1.386, 2.997, 
1.378, 2.186, 3.578, 4.254, 3.271, 4.313, 4.405, 2.795, 5.595, 
12.57, 3.092, 3.847, 2.163, 2.124, 3.362, 2.623, 12.17, 12.57, 
12.57, 3.162, 2.544, 4.050, 4.626, 4.764, 4.301, 5.215, 3.464)
dsm = daisy(x, metric="gower", type=list(asymm=c(5,16,17,20,23,
                              25,27,30,31,32,33,34)), weights=w)
summary(dsm)

这将产生

232903 dissimilarities, summarized :
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
 0.0000  0.2910  0.4212  0.4139  0.5327  1.0000
Metric :  mixed ;  Types = I, N, O, O, A, O, N, O, N, O, N, N, N, N, N, A, 
                  A, N, N, A, N, N, A, N, A, N, A, N, N, A, A, A, A, A, N
Number of objects : 683

调用 pam 创建 2 个聚类（k-medoids），并绘制结果

result <- pam(dsm, 2)
clusplot(result, col.p=result$clustering)

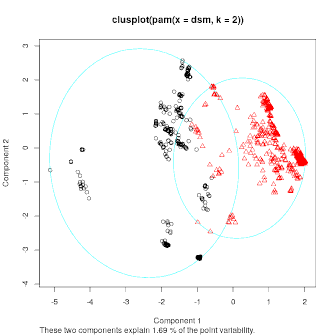
这看起来像 CLUELA 生成的输出。通过打印嵌入坐标来检查这一点

cmdscale(sqrt(dsm), add=FALSE)

这将产生

               [,1]          [,2]
  [1,] -0.218908503 -2.884794e-02
  [2,] -0.214924352 -2.570253e-02
  [3,] -0.205159906 -1.364315e-02
...

这证实了结果。退出 R。

q()

葡萄酒问题

葡萄酒数据集是全连续变量。N=178, P=13, K=3。让我们专注于尝试找到正确的聚类数量。在 [Pham, Dimov & Nguyen, 2005] 中，据报道他们提出的方法选择了正确的聚类数量。

作为第一次尝试，在原始数据上运行 CLUELA 会得到非常糟糕的准确率。更仔细地阅读期刊文章，我们注意到需要标准化输入。F 统计量的图现在显示最小值为 2，而不是 3。

更仔细地阅读期刊文章，Pham 等人运行的是他们自己特有的 k-means 变体，我们不打算复制。相反，我们将使用特殊的（*非常*特殊的）重要性权重。这些权重是通过优化 Bach-Jordan 谱聚类算法 [Bach & Jordan, 2003] 的残差获得的，使用 Richard Brent 的 PRAXIS 子例程。这不使用类别标签，但会引入偏差，因为权重是在 K=3 的假设下优化的。F 值现在显示最小值为 3，略小于 2 的值。

启示：一个好的统计学家可以证明任何事情。一个邪恶的统计学家也可以。普通 PCA 投影和稳健 PCA 投影之间存在微小的差异。

Dots in 3 color-coded groups. There is slight overlap.

信用审批问题

这是一个两类分类问题，有 15 个属性，这些属性已被故意模糊化。数据读取和重编码方式与前面类似。N=690, O=15, G=2, P=38。连续变量缩放到 0 到 1。权重设置为相等。

当使用 CLUELA 接口时，THRESH 设置为一个非常大的数字，并且 KCLUST 对每个从 KMIN 到 KMAX 的聚类数量重复 10 次。直接调用 KCLUST 会跳过重复项，并允许另一种确定聚类数量的方法。设置 K = 2。调用 DINIT 应用 kmeans++ 初始化，然后调用 KCLUST 使用 DINIT 返回的 THRESH 值。一个点如果离其最近的中心比 THRESH 远，则会成为一个新的中心。这会产生

kclust returns #0, made 2 clusters

接下来调用 DINIT，将 THRESH 除以 2，然后调用 KCLUST。这会产生

with half the threshold distance, kclust returns #0, made 4 clusters

程序运行发现了这些聚类

但存在相当大的偶然性！可以通过 MDS 在其欧几里得或曼哈顿距离上绘制类别

允许翻转水平轴，图形之间的差异很小。

问题“round” - 单位圆重访

t_round 程序在单位圆上随机生成 30,000 个点。我们在“数据聚类入门” [*] 中看到过这个问题，并使用其中介绍的简单 k-means 算法解决。现在有了 CLUELA，我们可以将这些结果与使用 ROBUST 和 SOSDO 选项的结果进行比较。

ROBUST 选项调用曼哈顿度量。这是一种非欧几里得几何，我们必须准备好接受在您的计算机监视器上这个近似欧几里得空间区域的结果图看起来会有些奇怪。

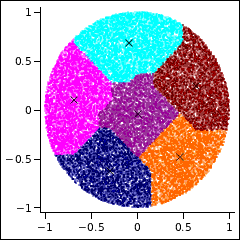
Pham 等人的 K 选择方法假定欧几里得空间。[Pham, Dimov & Nguyen, 2005] 在曼哈顿空间中，它没有显示出任何聚类趋势，这不足为奇。

设置 SOSDO 选项则返回了熟悉的结果。

F 值显示了形成三个聚类的趋势，这与 Pham 等人的结果一致。

对于大量的聚类，二叉树是一个重要的节省时间的方法。设置 K=1000 并比较 CLUSTE 和 KMNS。

 cluste returns #           0  in   0.677361012      seconds. Made         1000  clusters with residual    14.0591612    
 kmns returns #           0  in    1.31767201      seconds. Made         1000  clusters with residual    13.8801050

所以 CLUSTE 更快，但 KMNS 更准确。

马科疾病问题

此数据集有点困难。首先，可能存在一些错误。年轻/成年字段应编码为 {1,2}，但实际上是 {1,9}。这很容易修复，但仍然很奇怪。字段“毛细血管再充盈时间”应编码为 {1,2}，但包含值 3。这可能是一个错误，但如果我们不为该变量设置 CAT=3，RSCODE 将会失败。一些有序变量的顺序是错误的。例如

!       extremities temp   Ordinal             1 = Normal
!                                              2 = Warm
!                                              3 = Cool
!                                              4 = Cold

所以我们需要交换 1 和 2，这样序列就是 Warm, Normal, Cool, Cold。

horse-colic.both 中的三个属性是诊断代码。这些不是类别变量，因为诊断不是互斥的。一匹马可能患有一种以上的疾病。为了在 RSCODE 中表示这一点，需要将其转换为类别变量。首先，我们必须计算不同的诊断。有 62 种。每种可能的诊断都被视为一个二元变量。所以我们使用前 24 个属性，并将接下来的三个属性转换为 62 个变量，然后忽略属性 28。因此 N=368, O=24+62=86。

医院编号属性有 346 个不同的值。这太多了，需要转换为虚拟变量。我们可以看到，当类别数量变得非常大时，重编码是不可行的。一些分析师选择在这种情况下合并类别。完全省略此变量是合理的。也可以编写一个直接处理类别数据的距离函数，从而无需重编码。我们将承受重编码的后果，得到 P=440。

接下来，我们像以前一样重编码数据并调用聚类子例程。CLUELA 搜索一个好的聚类数量，从 KMIN=1 到 KMAX=20。似乎偏好两个聚类。

考虑以*原则性*方式选择重要性权重的集合。将一个点分配到一个聚类而不是另一个聚类是一个突然的转变，因此优化连续函数的最佳方法不适合。**模拟退火**是一种多功能的优化技术，并且易于应用。目标是最小化点到中心的总平方距离，但还有其他因素需要考虑。

权重必须约束为求和为 1，以免它们全部趋向于零。
必须有一个因子偏好相等性，以防止所有权重都集中在一个变量上的琐碎解决方案。
优化问题的难度随着变量数量的增加而急剧增加。要优化的权重应该是 25 个输入变量的权重，而不是 440 个重编码变量的权重。

目标函数然后是$ h = u \sum w_j^a $，其中*u*是 KCLUST 返回的残差，*w*是要优化的权重，*a*是分析师选择的指数。首先，对未加权数据进行聚类。Pham f 统计量的值显示偏好两个聚类

将惩罚指数 PEX=2 设置为导致一个非常分离的聚类

权重已集中在少数几个类别变量上。存在清晰的结构，但大量数据被忽略了。这不是我们想要的。尝试更强的惩罚* PEX=3。

penalty exponent 3.000000 and robust=F yield optimized weights:   
0.049  0.055  0.031  0.004  0.034  0.004  0.053  0.053  0.042  0.050  
0.022  0.054  0.053  0.051  0.051  0.042  0.052  0.045  0.017  0.002  
0.047  0.032  0.049  0.050  0.058

一些权重已被缩小到零附近，但大部分问题数据已被考虑在内。使用优化后的权重，使用 MDS 嵌入数据以填充缺失值，以便我们可以比较 CLUELA、CLUSTE、KMNS 和竞争对手的神经网络算法。**神经网络 (Neural Gas)** 算法 [Martinetz & Schulten, 1991] 等同于数据聚类。它的开发重点是学习数据空间的表示，而不是对数据集进行分区。输出到终端的是

cluela returns #0  Residual: 115.230087
cluste returns in 0.140965 seconds.  Residual: 115.230087
kmns returns in 0.024483 seconds. Residual: 115.223747
neugas returns in 0.055848 seconds.  Residual: 115.556557
program complete

图象通常是相同的。这些结果表明，在使用 SOSDO 选项时，CLUELA 的准确性与 KMNS 相同，但 KMNS 更快。对于 P 大 K 小的情况，CLUSTE 更慢。神经网络计算成本很高，但有效。

确定权重的方法是否令人满意？嗯，总比没有好。分析师仍然可以在选择惩罚指数、模拟退火参数、如何标准化连续属性以及是否使用稳健模式方面拥有自由裁量权。模拟退火是一种随机方法，因此每次运行程序的结果都不同。一个不诚实的统计学家可能会运行程序直到它返回他想要的答案。而且，无法区分选择权重和选择聚类数量的问题。

House Votes '84

众议院投票数据集记录了美国众议院 1984 年会议期间对某些法案的投票。目标是将每位代表归类为民主党或共和党。N=435, P=16, G=2。投票是“y”、“n”和“?”。我们首先尝试将问号视为缺失数据。CLUELA 返回 IFAULT=10，因为数据中存在一个空对象。国会中有人没有对任何这些法案投票。k-means 算法无法处理空对象。[*]

在这种情况下，有一个简单的解决方案。与其将投票视为类别数据，不如将其视为连续数据，令 n⇒0.0 ?⇒0.5 y⇒1.0

聚类结果在一定程度上与类别匹配。调整后的 Rand 指数为 0.58

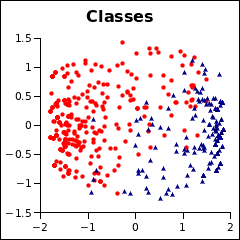
F 值显示出形成两个聚类的强烈趋势，这应该是符合预期的。

以稳健模式重复该问题。调整后的 Rand 指数变化不大。它是 0.53。嵌入完全不同

普通嵌入依赖于协方差矩阵，而稳健嵌入依赖于喜剧演员矩阵。离散变量的协方差矩阵是满矩阵，但喜剧演员矩阵可能包含许多零项，因此没有相似之处。

森林火灾问题

森林火灾数据包含葡萄牙自然保护区火灾过火面积的测量值。它记录了火灾地点、月份、星期几、温度、湿度、风速、降雨量以及一些用于预测火灾的统计数据。

月份和日期构成特殊挑战，因为它们是循环变量。十二月和一月之间的区别是一个月，而不是十一个月。CLUELA 不支持循环变量，但可以使用 MDS 进行嵌入。小程序 t_embed 创建一个 0 到 1 的一维数据集并将其嵌入为循环数据。这会产生许多维度，但前两个是最重要的。输出正是所期望的。多维缩放是一个非常强大的工具。

MDS 返回的第一个方向是最重要的，通常近似值就足够了。MDS 精确地表示原始距离，但必须使用所有 N 个方向。这有点棘手。要计算嵌入坐标，必须将不相似度矩阵的特征向量乘以相应特征值的平方根。对应于正特征值的方向是实方向。对应于负特征值的方向是*虚*方向。虚方向上两个对象之间的差异越大，它们就越接近。包含实方向和虚方向的数据集称为伪欧几里得 [Laub, 2004]，绝对不是度量空间。

CLUELA 只接受实数作为输入，但设置负权重将用于将变量视为虚数。森林火灾数据将被聚类三次，以比较将其视为线性、尊重仅使用实方向的循环属性以及尊重使用实方向和虚方向的循环属性的效果。由于过火面积非常偏斜，取其对数。将循环变量缩放到单位周期，连续变量缩放到单位范围。保持权重相等。将结果相互比较

Comparing the linear against pseudo-Euclidean:  
Adjusted Rand Index: 0.888586 
Variation of Information: 0.274069
Comparing the real embedding against pseudo-Euclidean:  
Adjusted Rand Index: 1.000000 
Variation of Information: 0.000000

因此，循环变量的影响很小。使用虚方向对结果没有任何影响。考虑伪欧几里得聚类，似乎有两个聚类

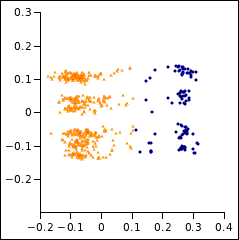
循环数据和虚坐标可能不特别有用，但它们肯定很有趣。

注释

有关 k-means 的介绍，请查阅 Wikipedia，或 Codeproject 上早期的文章 “数据聚类入门”，其中给出了一个简单的实现。
单变量拉普拉斯分布确实具有 L1 几何。所谓的多变量拉普拉斯分布 [Kotz, Kozubowski & Podgórski, 2001] 是椭球形的。在一维中，欧几里得度和曼哈顿度量无论如何都相同，因此可能没有良好的理论依据支持曼哈顿度量。
存在一些从相似性到非相似性的转换，计算速度更快，但反余弦函数是单位超球面上两点之间的弧长。这是一种度量非相似性，对于某些应用很重要。
当使用二分值进行非相似性计算时，必须将连续变量和有序变量缩放到 0...1，以使非相似性满足三角不等式。[Gower, 1971]
例如，维基百科在 2017 年 8 月 26 日提到，“标准算法旨在最小化 WCSS 目标，因此通过‘最小平方和’进行分配，这与通过最小欧几里得距离进行分配完全等价。”
如果所有数据都是连续的，那么每个变量的重要性可以通过将数据乘以一个标量来表示。由于无法对分类变量执行此操作，因此需要一个单独的数组来显示每个变量的重要性。
有人建议通过省略最后一个连续的虚拟变量来实现使用 c - 1 个变量的虚拟编码。[Bowles, 2015] 这会引入偏差，因为最后一类与其他类别之间的差异小于其他类别之间的差异。
数值上的困难是由于逻辑不一致。如果学习某物的存在是有信息的，那么学习它的不存在也必须是有信息的。（见附录）当然，这并不意味着信息含量相等，并且该领域的权威人士一直提倡使用二分变量。如果需要考虑信息含量，则应以有原则的方式进行，并从数据中推断，而不是由分析师通过其先验假设强加。
图聚类算法可以通过分配任意非相似性来处理空对象。
对循环变量进行聚类是可能的，但这会使整个软件包更加复杂，因此已删除支持。

道歉

每个人都会犯错，但不是每个人都承认。在修订版 3 之前，此软件包包含一个声称可以处理缺失数据的 PCA 版本，因为我当时认为可以进行简单的线性外插。问题在于，特征向量的分量可以是正的或负的，因此无法对省略其中一些分量的情况进行补偿。我已经用 MDS 替换了这种无效的处理方式，以正确处理缺失数据。替换后的 PCA 不接受缺失数据。旧版本中的非欧几里得协方差已被移除。

完美是良好的敌人，因此我将推出这款存在一些已知缺点的软件。

文件名 prep.f 和 prep.c 中的例程通过排序和比较相邻元素来查找重复项。要真正高效，应该使用哈希表来完成。
如果每一层的枢轴点是其祖先层枢轴点的一部分，则二叉树可以更有效。
过时的 EISPACK 例程仅适用于小型问题。要将 MDS 应用于包含数千个对象的数千个数据集，必须近似化非相似性矩阵。然后应使用 Lanczos 算法来查找特征向量。
HCLUST 分裂具有最大个体的簇，而不是具有最大直径的簇。
使用平均非相似性来处理缺失数据是一种尚未探索的可能性。

修订历史

2017 年 8 月 29 日
- 首次发布
2017 年 10 月 7 日
- 更改了 KCLUST 中删除簇的循环，使其成为负步长。这应该可以修复当需要删除多个簇时可能发生的错误
2017 年 11 月 8 日
- 修复了 USORTU 中当 N 等于 1 时返回无效索引的错误
2020 年 12 月 24 日
- 无效的缺失数据 PCA 被多维标度法取代。
- 二叉树搜索中的最大距离准则。
- 安全除法函数 SAFDIV 的替换。
- 移除补偿加法。
- 森林火灾问题取代枫叶舞曲问题。

下一步

数据聚类的直接路径是期望最大化。非相似性的概念被精确地定义为条件概率。Miller 等人（1994 年）提供了一个有用的案例研究。免费程序包括 McLachlan 和 Peel 的 EMMIX、Fraley 等人的 mclust 和 AUTOCLASS。

附录

二分变量是不合逻辑的：（归谬法）
A：观察到的事物
B：推断出的事物
给定：A 的存在会告知 B，而 A 的不存在对 B 没有信息量。
Pr(B|A) ≠ Pr(B)
Pr(B|¬A) = Pr(B)

点 Q 位于中心 O 的临界距离内 半距离引理：[Elkan, 2003] 如果一个点到其最近中心的距离小于或等于该中心到任何其他中心的距离的一半，则该点不属于任何其他簇。

证明：设 Q 为该点。设 O 为其当前中心。设 P 为 O 的最近中心。

给定：$\begin{aligned} & \left|OQ\right| \leq \frac{1}{2} \left|OP\right| \\ & 2 \left|OQ\right| \leq \left|OP\right| \end{aligned}$ 根据三角不等式，$\begin{aligned} & \left|OP\right| \leq \left|OQ\right| + \left|PQ\right| \\ & 2 \left|OQ\right| \leq \left|OP\right| \leq \left|OQ\right| + \left|PQ\right| \\ & \left|OQ\right| \leq \left|PQ\right| \end{aligned}$

用于攀登 GHT 的标准 广义超平面树公式：[Chávez, 1999] QS ≥ ½ |PQ - OQ|

证明：枢轴点是 O 和 P，查询点是 Q。S 是边界表面上的一个假想点。距离 |QS| 必须有界，以便将其与 r（包含 Q 的已知邻居的球体的半径）进行比较。

构造三角形 PQS，然后根据三角不等式：$ \left|QS\right| \geq \left|PQ\right| - \left|PS\right|$ 构造三角形 OQS，然后根据三角不等式：$ \left|QS\right| \geq \left|OS\right| - \left|OQ\right|$ 相加 $ 2 \left|QS\right| \geq (\left|PQ\right| - \left|OQ\right|) + (\left|OS\right| - \left|PS\right|)$ |OS| = |PS| 根据定义，$ \left|QS\right| \geq \frac{1}{2} (\left|PQ\right| - \left|OQ\right|)$

二等分树公式：[Kalantari, 1983] R < PQ - PF

枢轴点是 O 和 P，查询点是 Q。F 是远分区中距离枢轴点 P 最远的那个点。R 是 Q 周围的搜索半径。

如果距离 $ \overline{PQ} > \overline{PF} + R $ 那么远分区中的任何点都不会在搜索半径内。因此，如果 $ R < \overline{PQ} - \overline{PF} $ 则无需探索远分支。

广义超平面树不是本文的主题，但它们值得被更多人了解。这里是 INSERT 和 SELECT 操作的流程图。由于对象可能是枢轴点，因此无法执行 DELETE 操作。

Steps in the insert operation of a generalized hyperplane tree Steps in the Select operation on a generalized hyperplane tree

缺失数据是非度量的 三角不等式违反

反例证明：考虑缺失数据的曼哈顿非相似性函数

$ d(X,Y) = \frac{\sum W_{total}}{\sum W_{avail}} \sum \left|X_i - Y_i\right| $

考虑点 O = (0,0)、P = (3,4) 和 Q = (1,?)，并将权重设为相等。非相似性为
d(O,P) = (2/2) (|3-0| + |4-0|) = 7
d(O,Q) = (2/1) (|1-0| + ∅) = 2
d(P,Q) = (2/1) (|3-1| + ∅) = 4
2 + 4 < 7，三角不等式被违反。

平方距离总和的减少和增加：[Hartigan, 1979] 从一个大小为 N 的簇 C 中移除一个点 X 会使平方距离总和减少

$ d^2(X,C) \frac{N}{N-1} $

将一个点放入一个簇会使平方距离总和增加

$ d^2(X,C) \frac{N}{N+1} $

移除点的证明：设 X' 表示被转移的点。设 C' 表示簇中心的新的位置。设 X_i，1 ≤ i ≤ N 为簇中的初始点。那么平方距离 U 的变化为

$ \Delta U_{del} = \sum(X_i-C')^2 - \sum(X_i-C)^2 - (X'-C')^2 $ 展开：$ -2(\sum X_i)(C'-C) + \sum(C'^2-C^2) - (X'-C')^2 $ 进行一些代数运算表明：$\begin{aligned} & \sum X_i = NC \\ & C'-C = -\frac{X'-C}{N-1} \\ & C'^2-C^2 = \frac{(X'+C-2NC)(X'-C)}{(N-1)^2} \\ & X'-C' = \frac{N}{N-1}(X'-C) \end{aligned}$ 代入：$ \Delta U_{del} = -2NC\frac{-(X'-C)}{N-1} + N\frac{(X'+C-2NC)(X'-C)}{(N-1)^2} - (\frac{N}{N-1})^2 (X'-C)^2 $ 简化为：$ \Delta U_{del} = -(X'-C)^2 \frac{N}{N-1} $

将点插入的公式的推导留给感兴趣的读者。

平方和非相似性是非度量的

反例证明：假设有一个数据点 X 和两个相同的中心 C₁ 和 C₂
假设 X 是 C₁ 的一个元素，而不是 C₂ 的。那么

$d(X,C_1) > d(X,C_2)$ 但 $d(C_1,C_2) = 0 \\ d(X,C_1) > d(X,C_2) + d(C_1,C_2) $

三角不等式被违反。

正态单纯形坐标
1.000	0.500	0.500	0.500
0.000	0.866	0.289	0.289
0.000	0.000	0.816	0.204
0.000	0.000	0.000	0.791

L1 几何中的正态单纯形坐标
1.000	0.500	0.500	0.500
0.000	0.500	0.000	0.000
0.000	0.000	0.500	0.000
0.000	0.000	0.000	0.500

参考文献

Robert L. Thorndike, "Who Belongs in the Family?" Psychometrika, v.18 n.4, December 1953
Geoffrey H. Ball and David J. Hall, Isodata, a Novel Method of Data Analysis and Pattern Classification Stanford Research Institute Technical Report, Project 5533, April 1965. at DTIC
A. J. B. Anderson, "Similarity Measure for Mixed Attribute Types", Nature, v.232 pp.416-417, 6 Aug 1971.
John C. Gower, "A General Coefficient of Similarity and Some of Its Properties" Biometrics, v.28 n.4 pp.857-871, Dec. 1971. at JSTOR
John A. Hartigan and Manchek A. Wong, "Algorithm AS 136: A K-Means Clustering Algorithm" Applied Statistics v.28 n.1 pp.100-108, 1979. at JSTOR
R.S. Michalski and R.L. Chilausky, "Learning by Being Told and Learning from Examples: An Experimental Comparison of the Two Methods of Knowledge Acquisition in the Context of Developing an Expert System for Soybean Disease Diagnosis", International Journal of Policy Analysis and Information Systems, Vol. 4, No. 2, 1980.
I. Kalantari and G. McDonald, "A data structure and an algorithm for the nearest point problem" IEEE Transactions on Software Engineering, v.9 p.5, 1983
Congressional Quarterly Almanac, 98th Congress, 2nd session 1984, Volume XL: Congressional Quarterly Inc. Washington, D.C., 1985.
Glenn W. Milligan and Martha C. Cooper, "An Examination of Procedures for Determining the Number of Clusters in a Data Set" Psychometrika v.50 n.2 pp.159-179, June 1985.
M. Lichman (Admin.), UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science, 1987-present
Ross Quinlan, "Simplifying decision trees" Int J Man-Machine Studies v.27, pp. 221-234, December 1987
Mary McLeish & Matt Cecile, "Horse Colic Data Set", Department of Computer Science, University of Guelph, Guelph, Ontario, Canada N1G 2W1, [c.1989]
Leonard Kaufman and Peter J. Rousseeuw, Finding Groups in Data: An Introduction to Cluster Analysis, Wiley, 1990, reissued 2005.
M. Forina, et al, PARVUS - An Extendable Package for Data Exploration, Classification and Correlation. Institute of Pharmaceutical and Food Analysis and Technologies, Via Brigata Salerno, 16147 Genoa, Italy.[c.1991]
Jeffrey K. Uhlmann, "Satisfying General Proximity/Similarity Queries with Metric Trees" Information Processing Letters, v.40 pp.175-179, November 1991
Thomas Martinetz and Klaus Schulten, 'A "Neural-Gas" Network Learns Topologies' in Artificial Neural Networks, Ed. T. Kohonen, K. Makisara, O. Simula, and J. Kangas. Holland: Elsevier, 1991. at researchgate
J.W. Miller, W.A. Woodward, H.L. Gray & G.D. McCartor "A Hypothesis-Testing Approach to Discriminant Analysis with Mixed Categorical and Continuous Variables When Data Are Missing" Phillips Laboratory, [U.S.] Air Force Materiel Command, July 1994. at DTIC
Michael Falk, "On MAD and Comedians" Ann. Inst. Statist. Math. v.49 n.4 pp.615-644, 1997.
Zhexue Huang, "Clustering Large Data Sets With Mixed Numeric and Categorical Values" Canberra: CSIRO Mathematical and Information Sciences, 1997.
Maria Laura Carranza, Enrico Feoli & Paola Ganis, "Analysis of vegetation structural diversity by Burnaby's similarity index," Plant Ecology, v.138 pp.77-87, 1998. at researchgate:
Geoff McLachlan & David Peel "The EMMIX Algorithm for the Fitting of Normal and t-Components" Journal of Statistical Software, v.4 i.2, 12 July 1999. online
Edgar Chávez, Gonzallo Navarro, and José Luis Marroquín, "Searching in Metric Spaces" Association for Computing Machinery, 1999
Dan Pelleg and Andrew Moore, "X-means: Extending K-means with Efficient Estimation of the Number of Clusters." Draft report, 2000. at citeseerx
János Podani, Introduction to the Exploration of Multivariate Biological Data Leiden: Backhuys Publishers, 2000. online:
Samuel Kotz, Tomasz J. Kozubowski, and Krzysztof Podgórski, The Laplace Distribution and Generalizations: A Revisit with New Applications. Internet draft copy, 24 January 2001
Marina Meilă, "Comparing Clusterings" University of Washington, technical report, 2002. at citeseerx
Charles Elkan, "Using the Triangle Inequality to Accelerate k-Means" Proceedings of the Twentieth International Conference on Machine Learning, 2003. online
Francis R. Bach and Michael I. Jordan, "Learning Spectral Clustering" University of California, draft report, 2003. at École Normale Supérieure
Julian Laub, Non-Metric Pairwise Proximity Data Dipl. Ing. Phys. Thesis, Technical University of Berlin, 10 December 2004. at TU Berlin
D T Pham, S S Dimov, and C D Nguyen, "Selection of K in K-means Clustering" J. of Mechanical Engineering Science, 2005.
Shai Ben-David, Ulrike von Luxburg, and Dávid Pál, "A Sober Look at Clustering Stability", [c.2005] at citeseerx
Rafail Ostrovsky, Yuval Rabani, Leonard J. Schulman, and Chaitanya Swamy, "The Effectiveness of Lloyd-Type Methods for the k-means Problem", Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science, 2006. at University of Waterloo
Brendan McCane & Michael Albert, "Distance Functions for Categorical and Mixed Variables", Department of Computer Science, University of Otago, Dunedin, New Zealand, 14 Dec 2007. online Be warned that "symbolic covariance" proposed in this article is invalid.
P. Cortez and A. Morais, "A Data Mining Approach to Predict Forest Fires using Meteorological Data." In J. Neves, M. F. Santos and J. Machado Eds., New Trends in Artificial Intelligence, Proceedings of the 13th EPIA 2007 - Portuguese Conference on Artificial Intelligence, December 2007, Guimaraes, Portugal, pp. 512-523. APPIA, ISBN-13 978-989-95618-0-9. available:
David Arthur and Sergei Vassilvitskii, "k-means++: the advantages of careful seeding", Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, 2007. at Stanford
Sung-Hyuk Cha, "Comprehensive Survey on Distance/Similarity Measures between Probability Density Functions" International Journal of Mathematical Models and Methods in Applied Sciences v.1 i.4, 2007.
Shyam Boriah, Varun Chandola, and Vipin Kumar, "Similarity Measures for Categorical Data: A Comparative Evaluation" Proceedings of the SIAM International Conference on Data Mining, Atlanta, Georgia, USA, 24-26 April 2008. at researchgate
Hans-Hermann Bock, "Origins and extensions of the k-means algorithm in cluster analysis" Electronic Journ@l for History of Probability and Statistics v.4 n.2 December 2008 online
Michiel de Hoon, Seiya Imoto, and Satoru Miyano. Users' manual for: The C Clustering Library for cDNA Microarray Data, University of Tokyo, Institute of Medical Science, Human Genome Center, 27 December 2010. online
Michel Deza and Elena Deza, Distances in PR, Audio and Image Séminaire Brillouin, IRCAM, 31 May 2012. online
Brian Kulis and Michael I. Jordan, "Revisiting K-means: New Algorithms via Bayesian Nonparametrics" Proceedings of the 29th International Conference on Machine Learning, 2012. at researchgate
Malika Charrad, Nadia Ghazzali, Veronique Boiteau, and Adam Niknafs, "NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set" available from CRAN Journal of Statistical Software v.61 i.6 pp.1-36, 2014.
Michael Bowles, Machine Learning in Python: Essential Techniques for Predictive Analysis Wiley, 2015.