构建简单人工智能 .NET 库 - 第 2 部分 - 机器学习入门
4.84/5 (28投票s)
这是一系列从零开始演示.NET人工智能库的文章
系列介绍
这是创建.NET库的第二篇文章。以下是第一部分的链接
我的目标是创建一个简单的人工智能库,涵盖几个高级人工智能主题,如遗传算法、人工神经网络、模糊逻辑和其他进化算法。完成这个系列文章的唯一挑战是是否有足够的时间来编写代码和文章。
代码本身可能不是主要目标,然而,理解这些算法才是。希望它有一天能对某人有所帮助。
该系列将分为几部分发布,我还不确定具体几部分。无论如何,每一部分将侧重于一个关键主题,力求全面覆盖。
请随时评论和提问,以获得任何澄清,或希望能提出更好的方法。
文章介绍 - 第二部分“机器学习入门”
我认为单独介绍机器学习中的基本定义会更有益,因为我们将在后续文章中使用这些定义。
本文大部分内容将专门介绍机器学习的概念和不同术语,网上有大量资源可供进一步参考。
人工智能到底意味着什么
在讨论机器学习之前,让我们先定义人工智能的真正含义,并将人工智能的定义作为前进的起点。
人工智能有许多基于应用或待解决问题的定义,然而,最简单的、适用于所有情况的定义可能是:“人工智能是创造能够做出决策而不被明确编程的机器的能力”,换句话说,“构建具有某种形式决策能力的机器(或应用程序)”。
这是关于此的维基百科文章。
当人类开始面临非常复杂且难以预先编程的问题时,对人工智能的需求就开始了。例如,考虑自动驾驶汽车。如果唯一的方法是预先编程汽车可能遇到的每一种情况,那么这将是一项非常艰巨的任务。实际上,这几乎是不可能的。
因此,显然我们需要更特殊的算法来为汽车的主处理器植入某种智能。
想想抚养孩子,当然,一开始你会明确地指导和提供指示,但在某个阶段,由于人类的智能;孩子会开始从经验(无论是好是坏)中学习,所以学习是智能的一个非常重要的组成部分,因此,机器学习术语总是与人工智能相关联。
机器学习的含义
简单来说,机器学习是人工智能的一个领域,它研究一个问题:“机器或应用程序如何从经验中自动学习?”
机器学习是用于形成学习过程以及最终机器的人工智能部分的技能、算法和/或工具的集合。
回到婴儿的比喻,教婴儿的一种方法是给出例子或让他经历一些事情。在机器学习中也是如此,这被称为“监督学习”,这意味着我们首先通过提供训练集来训练机器。
每个训练集应由相同的输入集和正确的答案(称为标签)组成。利用不同的算法,机器可以迭代所有训练集,开始学习并构建人工智能,然后;它将能够预测(提供估计输出)任何相似数量的输入或做出决策。
但这并不是机器学习的唯一类型,还有另外两种常见类型
无监督学习- 没有可用的训练集,用于稍后将提到的特定类型的问题强化学习- 是另一种类型的机器学习,没有训练集,但是机器会根据完成的目标获得反馈。例如,对于玩国际象棋的人工智能应用程序,反馈可能是赢得或输掉比赛。
让我们详细了解每种类型以及它们的使用方式。
监督学习
再次强调,这是当我们拥有可用的训练集来训练我们的机器时(这就是“监督”一词的由来)。也许,现在是时候举一个真实的案例示例了,例如构建一个根据面积估算公寓价格的应用程序。
这是一个在许多人工智能参考资料中用于解释概念的经典例子,我将使用它。
因此,要构建这样的应用程序,我们需要一组代表公寓面积与价格的组合。当然,实际情况的价格会受到多个因素的影响,如位置、房间数量。但是,为了简化,我们将其他因素视为常数,对价格没有影响。
这是监督学习,因为我们从可用数据开始,我们的目标将是创建一个应用程序来学习这些数据,甚至通过获得更多经验(获得更多面积与价格的组合)来变得更智能。
最终,该应用程序将接收输入(公寓面积,单个输入)并预测输出(价格),这是一个连续的数字,这些类型的问题在人工智能中被称为“回归”。
你可以将回归看作是一个优化函数或找到一个最佳拟合函数来映射输入到输出。在代数中,有一个称为“插值”的概念,它基本上是相同的概念,为给定的输入和输出集找到一个最佳拟合函数。
当然,这种映射可以是线性的或非线性的(取决于问题的复杂性)。线性回归是最简单的,它将映射函数表示为线性或直线。在人工智能术语中,映射函数称为假设或 h 函数,形式为 h(x) = a + b * x,其中
X是输入a & b是直线的斜率h(x)是输入的假设函数,或简单地说,是估计的输出
让我们将任何给定训练集的正确答案命名为 y,那么误差将是估计答案(假设)与正确答案之间的差值 e = h(x) - y。
从逻辑上讲,这个误差应该尽可能地最小化,以确保实现最佳拟合。误差最小化是一个包含许多算法的整个研究领域,我将在本文稍后继续讨论。
现在回到监督学习,我们已经看到回归是监督学习的一种应用,但它不是唯一的。请记住,回归处理的是连续(或实数)输出。那么离散输出的情况呢?例如,如果我们有一个包含几个输入的训练集,而输出只是将输入分组到预定义的组中,或者称为**分类**,这是监督学习的第二个主要应用。
无监督学习
另一方面,无监督学习没有预给的训练集,只有一组没有标签的输入(记住标签是正确的答案)。这种机器学习用于一类特定的问题,我们无法真正标记输入或预先编程。让我们以社交媒体为例。例如,YouTube 的推荐列表或 Facebook 的推荐朋友。
无监督机器学习可能就是这种人工智能的幕后推手,它会查看和排序每个用户的观看历史或好友列表。这在人工智能中被称为**聚类**问题。你可以想象,无法提前为每个用户编程这些推荐。
强化学习
对于第三种类型,它是一种特殊的监督学习版本,机器从结果或其自身经验中学习。它是从输出的反馈中学习(例如赢得或输掉一场比赛,或到达一个目的地)。
例如,考虑构建一个下棋应用程序。一方面,无法在任何给定时间编程所有可能的走法。另一方面,如果我们能够构建一个应用程序来玩每一场比赛并从输赢中学习,那么这就是强化学习类型。
下一步是什么
以上主要是机器学习的基础,在此基础上,建立了大量的算法和技术来确立每种类型并相应地解决不同的问题。
理解这一点很重要,因为这将有助于理解任何进一步与人工智能相关的进阶主题。
接下来的方向是探索不同的算法和方法,希望能进一步理解人工智能。
那么,现在是时候用代码构建我们的第一个人工智能算法了。
线性回归示例
让我们创建一个应用程序来解决一个简单的线性回归问题。无论应用程序的技术背景如何,或者我们试图解决的确切问题是什么,算法始终是相同的。因此,我们不会过多担心这些数据是什么,而是假设我们以某种方式获得了它。这是手头的数据
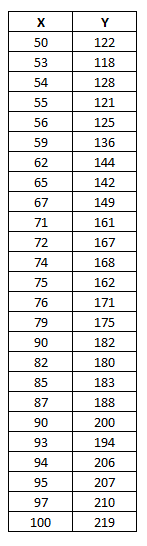
其中 X 是输入(可以是任何实数变量),Y 是正确的目标或标签。绘制这个数据集将得到

应用程序的目标是根据给定的训练集,预测例如当 x 为 70 时的输出。
根据给定的数据集,线性回归似乎是解决这个问题的可接受的方案。因此,应用程序将主要解决假设函数 h(x) = a + b * x,换句话说,找到 a 和 b 的值,它们产生最佳拟合线。
让我们为此构建算法,首先从任何随机值 a 和 b 开始。
''' <summary>
''' Linear Regression Pseudo Algorithm to resolve h(x) = a + b * x
''' 1- Start with random values for a and b
''' 2- Iterate through given training set, for each:
''' - Calculate h(x)
''' - Calculate error = h(x) - Y where y is the correct answer or label
''' 3- Sum all errors
''' </summary>
现在,我们需要将误差最小化到尽可能低的值,但首先,让我们消除负误差,误差可能朝两个方向,正向或负向。一种方法是计算误差之和的平方。
一些误差比其他误差高,这取决于正确答案和 h(x) 之间的差异,为了确保大多数误差都被关注,让我们取平均平方误差,即平方误差/训练集大小。
根据统计术语,这种方法称为“均方误差”或 MSE,它告诉您回归线与训练集的接近程度。

一些参考资料可能将 MSE 称为成本函数,这是一个更广泛的定义
其中 m 是训练集的大小(有多少训练组合)
由于这是一个二次多项式方程(假设只有一个变量),所以在二维坐标系中,这就是图
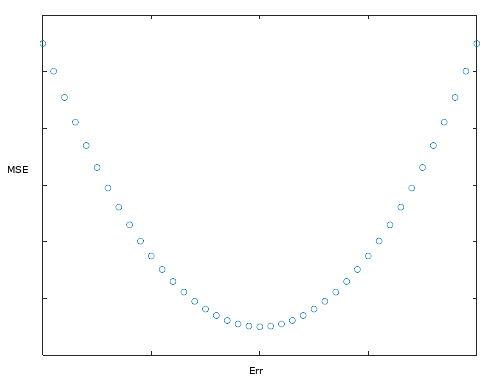
从上图可以看出,该函数只有一个最小值(我们现在还不知道这个最小值在哪里)。换句话说,上图告诉我们,如果我们从任何随机值 a 和 b 开始,我们将在上图的某个地方出现误差,然后我们需要移动到最小值。
在下图,蓝色点代表最小误差值,对于任何随机的 a 和 b 值,我们可能会落在右侧(如红圈)或左侧(如绿圈)。

问题是我们如何确定我们在曲线上的哪个位置?右边还是左边?
一种确定方向的方法是画一条与曲线在起始点相切的直线,然后计算这条直线的斜率。

例如,上图中的红线具有正斜率(向右移动时,直线值增加),而绿线具有负斜率。
让我们回顾一下我们的伪算法
''' <summary>
''' Linear Regression Pseudo Algorithm to resolve h(x) = a + b * x
''' 1- Start with random values for a and b
''' 2- Iterate through given training set, for each:
''' - Calculate h(x)
''' - Calculate error = h(x) - Y where y is the correct answer or label
''' 3- Sum all errors
''' 4- Calculate MSE (Mean Squared Error) = 1/2*training set size * sum of all errors
''' 5- Get slope of line touching curve at the current point (for each value of a and b)
''' - If +ve slope, move to left or Decrease a or b values
''' - If -ve slope, move to right or increase a or b values
''' 6- Repeat above steps from 2 to 5 till direction or slope of calculated line changes
''' 7- Last values for a and b are the optimal values as per MSE minimization
''' </summary>

以上是一个非常常见且实用的算法,称为**梯度下降**。然而,上述版本主要适用于线性回归,对于非线性函数需要考虑其他因素。
那么,我们如何计算直线的斜率呢?
与函数(曲线)在某一点相切的直线的斜率正好是函数导数的定义。在我们的例子中,我们有两个变量(a 和 b),这被称为偏导数。
梯度下降
到目前为止,我们有以下内容



让我们开始解决 a





长话短说,这是 a 的最终偏导数

这是 b 的

那么

为了进一步控制步长,让我们添加一个小的数字来表示要采取的步长,作为斜率的比例。这称为“学习率”。学习率值不当会影响我们算法的最终行为,我们应该在代码中检查不同的值。
总之,让我们将其标记为 r

b 类似

以上最后两个方程代表了将梯度下降应用于线性回归的最终结论。
Using the Code
为了演示上述内容,我创建了一个简单的程序

主函数是 Train,它接受两个一维矩阵作为训练集
Public Sub Train(_Inputs As Matrix1D, _Labels As Matrix1D)
Dim m As Integer = _Inputs.Size ' Training set size
Dim Err As Matrix1D ' represents sum of all errors in single iteration
Dim Counter As Integer = 0
Dim Best_a, Best_b As Single
If _Inputs.Size <> _Labels.Size Then
Throw New Exception("Both Inputs and Labels Matrices sizes shall match.")
End If
' Randomize a & b
Randomize()
' Iterate and update a & b values till direction changes
Do While Counter < 100
Dim h_Matrix As New Matrix1D(m)
' Calculate Error matrix
Err = New Matrix1D(m)
For I As Integer = 0 To m - 1
h_Matrix.SetValue(I, Hypothesis(_Inputs.GetValue(I)))
Next
Err = h_Matrix.Sub(_Labels)
If CalcCostFunction(Err) < min_MSE OrElse Counter = 0 Then
min_MSE = CalcCostFunction(Err)
Best_a = a
Best_b = b
End If
a = a - r * (1 / m) * Err.Sum
Err = Err.Product(_Inputs)
b = b - r * (1 / m) * Err.Sum
Counter += 1
Loop
a = Best_a
b = Best_b
End Sub
它实现了梯度下降的伪算法。
有不同的方法可以终止迭代,我选择了一种技术,设置最大计数器为 100,同时记录每次迭代中的最小 MSE 以及 Best_a 和 Best_b 变量。
最后,我需要提到样本软件引用了 `CommonLib`,该库已在文章开头添加(附带的版本是最新的)。
回顾
我们定义了三种类型的机器学习
监督学习- 具有可用的训练集,主要用于回归和分类问题无监督学习- 没有可用的训练集,通常用于聚类问题强化学习- 没有训练集,但机器通过每次经验的结果或反馈来学习
然后,我们详细介绍了一种关键的算法——梯度下降,通常用于线性回归,并提供了一个示例软件。
我不确定以上内容是否足够清晰,请告诉我。
下一篇文章
大部分内容将围绕监督学习的第二个应用,即分类,通常使用感知器。
历史
- 2017年9月10日:初版
