机器学习基础和感知器学习算法
4.91/5 (23投票s)
机器学习和感知器学习算法的基础。
机器学习是软件行业中人们经常谈论的一个术语,并且它日益流行。媒体上充斥着许多花哨的机器学习相关词汇:深度学习、OpenCV、TensorFlow等等。甚至非软件行业的人们也在尝试利用机器学习的力量。它在各行各业的应用日益广泛也就不足为奇了。
然而,当我们的头脑中充满了如此多令人惊叹的机器学习思想和术语时,我们很容易忽视或仅仅忘记机器学习的基本原理。本文旨在不仅回顾机器学习的基本原理,而且为初次学习机器学习的人提供一个简要的机器学习概念,以便他们了解什么是机器学习、它是如何工作的、如何做好它,并认识到机器学习并非魔法。
希望经验丰富的读者能从回顾机器学习的基本概念中受益,新手能从本文中获得机器学习的基本思想。
什么是机器学习?它能做什么?
机器学习是人工智能的一个子领域。顾名思义,它试图帮助机器从数据中“学习”一些东西。回想一下我们小时候是如何学会识别动物,例如狗的?我们可能从阅读一本包含狗图片(即数据)的书开始,然后我们遇到狗后就知道它是一只狗。这就是机器学习的本质:从数据中学习。
通过例子解释概念总是更容易。几年前我参加的这个 Kaggle 竞赛,预测拨款申请,旨在奖励能够提供模型来简化和加速审查流程以降低成本的参与者。
确定申请人是否符合拨款条件的传统方法是,学术评审员花费时间审查申请人的文件并做出决定。这个过程需要相当长的时间;特别是这所学校声称大部分申请最终都被拒绝。宝贵的学术评审员时间被浪费了。
这就是机器学习可以提供帮助的地方。机器学习方法可以初步筛选出机器学习方法预测有很高成功机会的申请。因此,评审委员会可以将时间花在这些候选人身上。
因此,机器学习的主要目标是通过用上下文相关数据训练数学模型来推断未来或做出决策。
它是如何工作的?
机器学习始于数据。在回答这个问题之前,我们首先看看数据。下表描绘了“预测拨款申请数据集”的摘录。该表演示了机器学习领域中常用的符号,例如样本、特征和标签。

那么,机器学习是如何工作的呢?首先,在“预测拨款申请”的例子中,每个人都会同意某些属性比其他属性具有更重要的权重。同样,在审查过程中,学术评审员可能会觉得某些属性比其他属性更重要。例如,期刊文章的数量可能比申请人的个人 ID 更重要。这一事实意味着存在成功申请的模式。其次,即使我们知道模式存在,也无法(或非常困难)写出一个数学公式来决定谁会获得资助。否则,我们只需使用数学公式编写程序来一次性解决这个问题。第三,这所学校有该项目的历史记录,即他们有数据。这些因素总结了使用机器学习解决问题的性质,如果问题具有以下特征:
- 存在某种模式。(在此预测拨款申请示例中,评审员觉得某些属性比其他属性更重要。)
- 没有简单的方法通过数学方程解决此问题。(这可能是我们需要机器学习方法的主要原因。如果我们能找到一个数学公式解决方案,它总是优于机器学习解决方案。)
- 我们有数据。(在此示例中,墨尔本大学有申请的历史记录;没有数据,机器学习无能为力。)
一旦问题满足这三点,机器学习就可以解决这个问题了。一个基本的机器学习方法包含以下组件。
- 目标函数:一个未知的理想函数。它存在,但未知
- 包含所有可能函数的假设集。例如,感知器、神经网络、支持向量机等等。
- 基于数据从假设集中选择最优函数的学习算法。例如,感知器学习算法、反向传播、二次规划等等。
- 学习模型:通常,假设集和学习算法的组合可以被称为一个学习。

有许多工具,即学习模型,可以解决机器学习问题。因此,第一步是选择一个学习模型来开始。每个学习模型都有其优点和缺点;有些可能擅长某个问题;有些可能不擅长。如何选择合适的学习模型超出了本文的讨论范围,但至少我们可以始终选择一个作为起点。
一旦选择了学习模型,我们就可以通过输入数据来训练模型。再次以“预测拨款申请”为例;这个过程从随机因素(即每个属性的权重)开始。然后通过输入历史记录,不断调整这些因素,使它们越来越符合学术评审员之前审查申请的方式,直到它们最终能够预测评审员通常如何决定申请人是否获得资助。这个过程就是所谓的模型训练。
模型训练完成后,该模型可以通过输入新数据来预测结果。在“预测拨款申请”示例中,新数据可能是当年的申请。大学可以使用此模型筛选出不太可能成功的申请,以便评审委员会可以专注于成功机会高的申请。
机器学习方法的一个优点是,它可以推广到更多维度中的更大规模数据集。当问题维度较低,即属性数量较少时,这很简单。然而,现实是墨尔本大学提供的数据集有249个特征,这使得这个问题变得更加困难(几乎不可能将其归结为一个简单的数学公式)。幸运的是,机器学习的强大之处在于它可以直接应用于具有更多特征的数据,并对其进行评估。
下一节将使用可能是最简单的学习模型来演示机器学习方法的基本工作流程。
一个简单示例:感知器学习算法
本例使用一个经典数据集,Iris 数据集,它包含三类,每类50个实例,每类指代一种鸢尾花。本例的目标是使用机器学习方法构建一个程序来分类鸢尾花的类型。
问题设置
Iris 数据集包含三个类别(类别通常也可以称为标签):Iris Setosa、Iris Versicolour 和 Iris Virginica。
除了类别,每个实例还具有以下属性:
- 萼片长度(厘米)
- 萼片宽度(厘米)
- 花瓣长度(厘米)
- 花瓣宽度(厘米)
Iris 数据集中的每个实例,也称为样本,看起来像 (5.1, 3.5, 1.4, 0.2, Iris-setosa)

本例选择的学习模型是感知器和感知器学习算法。
感知器学习算法
感知器学习算法是人工神经网络最简单的形式,即单层感知器。感知器是一种人工神经元,被认为是生物神经元的模型,生物神经元是人工神经网络中的基本单元。人工神经元是某些(一个或多个)输入和相应权重向量的线性组合。也就是说,感知器具有以下定义:
给定一个包含训练数据集 ![]() 和输出标签
和输出标签 ![]() 的数据集
的数据集 ![]() ,它可以构成一个矩阵。
,它可以构成一个矩阵。

每个 ![]() 是
是 ![]() 的一个样本,
的一个样本,![]()
每个 ![]() 是实际标签,具有二进制值:
是实际标签,具有二进制值:![]() 。
。
![]() 是权重向量。每个
是权重向量。每个 ![]() 都有一个对应的权重
都有一个对应的权重 ![]()
由于感知器是 ![]() 和
和 ![]() 的线性组合,它可以表示为
的线性组合,它可以表示为 
对于每个神经元 ![]() ,输出为
,输出为  ,其中
,其中 ![]() 是传递函数
是传递函数

为简单起见,![]() 可以视为
可以视为 ![]() ,其中
,其中 ![]()
因此,![]() 和
和 ![]() 的线性组合可以改写为
的线性组合可以改写为 
第 j 个神经元的输出为  ,其中
,其中 ![]() 是传递函数
是传递函数

学习步骤

根据感知器的定义,感知器学习算法按以下步骤工作:
- 将权重初始化为0或小的随机数。
- 对于每个训练样本
 ,执行以下子步骤:
,执行以下子步骤:- 计算
 ,即
,即  和
和  的线性组合,以获得预测输出,即类别标签
的线性组合,以获得预测输出,即类别标签 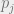 。
。 - 更新权重

- 记录错误分类的数量
- 计算
- 如果在训练完整个数据集
 后,错误分类的数量不为 0,则重复步骤 2 并从训练集的开头开始,即从
后,错误分类的数量不为 0,则重复步骤 2 并从训练集的开头开始,即从 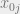 开始。重复此步骤直到错误分类的数量为 0。
开始。重复此步骤直到错误分类的数量为 0。
注意:
2.1 的输出是 ![]() 函数预测的类别。
函数预测的类别。
在步骤 2.2 中,![]() 的每个权重
的每个权重 ![]() 的更新遵循以下规则:
的更新遵循以下规则:
![]() ,其中
,其中 ![]() 表示步骤:
表示步骤:![]() 表示当前步骤,
表示当前步骤,![]() 表示下一步。因此,
表示下一步。因此,![]() 表示当前权重,
表示当前权重,![]() 表示更新后的权重。
表示更新后的权重。
如果没有错误分类,![]() 或
或 ![]() 。在这种情况下,
。在这种情况下,![]() 。不更新。
。不更新。
如果分类错误,![]() 或
或 ![]() 。在这种情况下,
。在这种情况下,![]() 或
或 ![]() 。权重更新。
。权重更新。
在步骤2.3中,PLA 的收敛性仅在两个类线性可分时得到保证。如果它们不可分,PLA 将永不停止。一个简单的修改是 Pocket 学习算法,我们将在未来的文章中讨论它。
感知器学习算法可以简单地实现如下:
import numpy as np
class PerceptronClassifier:
'''Preceptron Binary Classifier uses Perceptron Learning Algorithm
to do classification with two classes.
Parameters
----------
number_of_attributes : int
The number of attributes of data set.
Attributes
----------
weights : list of float
The list of weights corresponding <
g class="gr_ gr_313 gr-alert gr_gramm gr_inline_cards gr_run_anim
Grammar multiReplace" id="313" data-gr-id="313">with&
lt;/g> input attributes.
errors_trend : list of int
The number of misclassification for each training sample.
'''
def __init__(self, number_of_attributes: int):
# Initialize the weigths to zero
# The size is the number of attributes plus the bias, i.e. x_0 * w_0
self.weights = np.zeros(number_of_attributes + 1)
# Record of the number of misclassify for each train sample
self.misclassify_record = []
self._label_map = {}
self._reversed_label_map = {}
def _linear_combination(self, sample):
'''linear combination of sample and weights'''
return np.inner(sample, self.weights[1:])
def train(self, samples, labels, max_iterator=10):
'''Train the model
Parameters
----------
samples : two dimensions list
Training data set
labels : list of labels
Class labels. The labels can be anything as long as it has
only two types of labels.
max_iterator : int
The max iterator to stop the training process
in case the training data is not converaged.
'''
# Build the label map to map the original labels to numerical labels
# For example, ['a', 'b', 'c'] -> {0 : 'a', 1 : 'b', 2 : 'c'}
self._label_map = {1 : list(set(labels))[0], -1 : list(set(labels))[1]}
self._reversed_label_map = {value : key for key, value in self._label_map.items()}
# Transfer the labels to numerical labels
transfered_labels = [self._reversed_label_map[index] for index in labels]
for _ in range(max_iterator):
misclassifies = 0
for sample, target in zip(samples, transfered_labels):
linear_combination = self._linear_combination(sample)
update = target - np.where(linear_combination >= 0.0, 1, -1)
# use numpy.multiply to multiply element-wise
self.weights[1:] += np.multiply(update, sample)
self.weights[0] += update
# record the number of misclassification
misclassifies += int(update != 0.0)
if misclassifies == 0:
break
self.misclassify_record.append(misclassifies)
def classify(self, new_data):
'''Classify the sample based on the trained weights
Parameters
----------
new_data : two dimensions list
New data to be classified
Return
------
List of int
The list of predicted class labels.
'''
predicted_result = np.where((self._linear_combination(new_data) +
self.weights[0]) >= 0.0, 1, -1)
return [self._label_map[item] for item in predicted_result]
将感知器学习算法应用于 Iris 数据集
通常,将机器学习算法应用于数据集的第一步是将数据集转换为机器学习算法可以识别的某种形式或格式。这个过程可能涉及归一化、降维和特征工程。例如,大多数机器学习算法只接受数值数据。因此,数据集需要转换为数值格式。
在 Iris 数据集中,萼片长度、萼片宽度、花瓣长度和花瓣宽度这些属性是数值,但类别标签不是。因此,在 `PerceptronClassifier` 的实现中,训练函数将类别标签转换为数值格式。一个简单的方法是使用数字来表示这些标签:,这意味着 0 表示 Setosa,1 表示 Versicolour,2 表示 Virginica。然后,Iris 数据集可以被视为以下形式,以输入感知器学习算法。
![]()
![]()
感知器是二元分类器。然而,Iris 数据集有三个标签。处理多类别问题有两种常见方法:一对多(one-vs-all)和一对一(one-vs-one)。对于本节,我们使用简化的“一对一”策略来确定鸢尾花的类型。
一对一方法为每对类别训练一个模型,并通过多数投票来确定正确的类别。例如,Iris 数据集有三个类别。这意味着这三个类别两两组合的所有情况。即 ![]() 。
。
此外,机器学习不限于使用数据集中的所有特征。相反,只需要重要的特征。这里,我们只考虑萼片宽度和花瓣宽度这两个特征。事实上,选择正确的特征非常重要,以至于有一个专门的学科叫做特征工程来处理这个问题。
import numpy as np
import pandas as pd
import urllib.request
from perceptronlib.perceptron_classifier import PerceptronClassifier
# Download Iris Data Set from http://archive.ics.uci.edu/ml/datasets/Iris
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
urllib.request.urlretrieve(url, 'iris.data')
# Use pandas.read_csv module to load iris data set
# https://pandas.ac.cn/pandas-docs/stable/generated/pandas.read_csv.html
IRIS_DATA = pd.read_csv('iris.data', header=None)
# Prepare the training data and test data
# The original Iris Data Set has 150 samples and 50 samples for each class
# This example takes first 40 samples of each class as training data,
# and the other 10 samples of each class as testing data.
# So, this example uses the testing data to verify the trained Perceptron learning model.
# 0 ~ 39: setosa training set
# 40 ~ 49: setosa testing set
# 50 ~ 89 versicolor training set
# 90 ~ 99: versicolor testing set
# 100 ~ 139: virginica training set
# 140 ~ 149: virginica testing set
# Use pandas iloc to select samples by position and return an one-dimension array
# https://pandas.ac.cn/pandas-docs/stable/generated/pandas.DataFrame.iloc.html#pandas.DataFrame.iloc
SETOSA_LABEL = IRIS_DATA.iloc[0:40, 4].values
VERSICOLOR_LABEL = IRIS_DATA.iloc[50:90, 4].values
VIRGINICA_LABEL = IRIS_DATA.iloc[100:140, 4].values
SETOSA_VERSICOLOR_TRAINING_LABEL = np.append(SETOSA_LABEL, VERSICOLOR_LABEL)
SETOSA_VIRGINICA_TRAINING_LABEL = np.append(SETOSA_LABEL, VIRGINICA_LABEL)
VERSICOLOR_VIRGINICA_TRAINING_LABEL = np.append(VERSICOLOR_LABEL, VIRGINICA_LABEL)
# In this example, it uses only Sepal width and Petal width to train.
SETOSA_DATA = IRIS_DATA.iloc[0:40, [1, 3]].values
VERSICOLOR_DATA = IRIS_DATA.iloc[50:90, [1, 3]].values
VIRGINICA_DATA = IRIS_DATA.iloc[100:140, [1, 3]].values
# Use one-vs-one strategy to train three classes data set, so we need three binary classifiers
# setosa-versicolor, setosa-viginica, and versicolor-viginica
SETOSA_VERSICOLOR_TRAINING_DATA = np.append(SETOSA_DATA, VERSICOLOR_DATA, axis=0)
SETOSA_VIRGINICA_TRAINING_DATA = np.append(SETOSA_DATA, VIRGINICA_DATA, axis=0)
VERSICOLOR_VIRGINICA_TRAINING_DATA = np.append(VERSICOLOR_DATA, VIRGINICA_DATA, axis=0)
# Prepare test data set. Use only Sepal width and Petal width as well.
SETOSA_TEST = IRIS_DATA.iloc[40:50, [1, 3]].values
VERSICOLOR_TEST = IRIS_DATA.iloc[90:100, [1, 3]].values
VIRGINICA_TEST = IRIS_DATA.iloc[140:150, [1, 3]].values
TEST = np.append(SETOSA_TEST, VERSICOLOR_TEST, axis=0)
TEST = np.append(TEST, VIRGINICA_TEST, axis=0)
# Prepare the target of test data to verify the prediction
SETOSA_VERIFY = IRIS_DATA.iloc[40:50, 4].values
VERSICOLOR_VERIFY = IRIS_DATA.iloc[90:100, 4].values
VIRGINICA_VERIFY = IRIS_DATA.iloc[140:150, 4].values
VERIFY = np.append(SETOSA_VERIFY, VERSICOLOR_VERIFY)
VERIFY = np.append(VERIFY, VIRGINICA_VERIFY)
# Define a setosa-versicolor Perceptron() with 2 attributes
perceptron_setosa_versicolor = PerceptronClassifier(2)
# Train the model
perceptron_setosa_versicolor.train(SETOSA_VERSICOLOR_TRAINING_DATA,
SETOSA_VERSICOLOR_TRAINING_LABEL)
# Define a setosa-virginica Perceptron() with 2 attributes
perceptron_setosa_virginica = PerceptronClassifier(2)
# Train the model
perceptron_setosa_virginica.train(SETOSA_VIRGINICA_TRAINING_DATA,
SETOSA_VIRGINICA_TRAINING_LABEL)
# Define a versicolor-virginica Perceptron() with 2 attributes
perceptron_versicolor_virginica = PerceptronClassifier(2)
# Train the model
perceptron_versicolor_virginica.train(VERSICOLOR_VIRGINICA_TRAINING_DATA,
VERSICOLOR_VIRGINICA_TRAINING_LABEL)
# Run three binary classifiers
predict_target_1 = perceptron_setosa_versicolor.classify(TEST)
predict_target_2 = perceptron_setosa_virginica.classify(TEST)
predict_target_3 = perceptron_versicolor_virginica.classify(TEST)
overall_predict_result = []
for item in zip(predict_target_1, predict_target_2, predict_target_3):
unique, counts = np.unique(item, return_counts=True)
temp_result = (zip(unique, counts))
# Sort by values and return the class that has majority votes
overall_predict_result.append(sorted
(temp_result, reverse=True, key=lambda tup: tup[1])[0][0])
# The result should look like:
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-setosa', 2), ('Iris-versicolor', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-versicolor', 2), ('Iris-virginica', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# [('Iris-virginica', 2), ('Iris-versicolor', 1)]
# Verify the results
misclassifier = 0
for predict, verify in zip(overall_predict_result, VERIFY):
if predict != verify:
misclassifier += 1
print("The number of misclassifier: " + str(misclassifier))
完整的代码可在 https://github.com/burpeesDaily/ml-toybox/blob/main/mltoolbox/perceptron_classifier.py 找到。
学习是否可行?
许多人可能认为机器学习是魔法。但它不是。事实上,机器学习完全是关于数学,尤其是概率和统计。
学习 vs. 记忆
为了说明学习是否可行,我们需要定义什么是学习?在“一个简单示例”一节中,感知器学习算法最终成功地分类了所有的鸢尾花,但这真的是学习吗?或者,它只是记忆?为了回答这些问题,我们定义了样本内误差(in-sample error)和样本外误差(out-of-sample error)。样本内误差是指样本内的错误率。例如,最终,感知器学习模型可以分类 Iris 数据集中所有的鸢尾花。它的样本内误差为 0,即完全没有错误。与样本内误差相反,样本外误差是指样本之外的错误率。换句话说,它表示学习模型看到新数据时的错误数量。以相同的例子为例,如果我们向感知器学习模型输入新数据,错误分类率就是它的样本外误差。因此,要说一个学习模型是真正的学习,不仅样本内误差必须很小,而且样本外误差也必须很小。
那么,学习是否可行?
简单的答案是肯定的:从数学意义上讲,学习是可行的。
在概率论和统计学中,有两个重要的理论可以简要说明学习是可行的:中心极限定理和大数定律。中心极限定理指出,大量独立同分布变量的平均值分布将近似服从正态分布,无论其底层分布如何。大数定律描述了随着样本数量的增加,结果的平均值应该接近期望值,并且随着试验次数的增加会趋于更接近。数学理论保证了样本比例或样本比例差异将遵循类似于正态分布的分布,只要:1. 样本中的观察值是独立的。2. 样本足够大。以过度简化的方式来说,我们在样本中看到的学习结果应该在样本外数据中也能看到。因此,学习是可行的。
当然,这种说法过于简化。支持机器学习可行性的理论细节超出了本文的讨论范围。有许多资源可以探讨这个主题。我推荐的一本书是《从数据中学习》,特别是第2章 VC 维到泛化。
简而言之,要使学习可行,学习模型必须达到:
- 样本内误差小
- 样本外误差接近样本内误差
我们如何判断学习是否良好?
前一节“学习是否可行”的结论指出,如果样本内误差小且样本外误差接近样本内误差,则学习模型学到了一些东西。那么,样本内误差小和样本外误差接近样本内误差意味着什么?样本内误差应该有多小,样本外误差可以有多接近?当然,如果样本内误差和样本外误差都为零,那么学习模型就学习得非常完美。不幸的是,大多数现实世界的问题并非如此。事实上,机器学习方法并不是寻找理想目标函数;相反,机器学习方法寻找一个近似于目标函数 ![]() 的假设函数
的假设函数 ![]() 。(目标函数始终是未知的;否则,我们就不必费心使用机器学习方法了。)换句话说,机器学习方法寻找一个足够好的解决方案
。(目标函数始终是未知的;否则,我们就不必费心使用机器学习方法了。)换句话说,机器学习方法寻找一个足够好的解决方案 ![]() ,它足够接近
,它足够接近 ![]() 。足够好是什么意思?为了量化
。足够好是什么意思?为了量化 ![]() 与
与 ![]() 的接近程度,我们需要一种方法来定义
的接近程度,我们需要一种方法来定义 ![]() 和
和 ![]() 之间的距离。通常,这被称为误差度量或误差函数(误差也称为成本或风险)。
之间的距离。通常,这被称为误差度量或误差函数(误差也称为成本或风险)。
误差度量
通常,我们通过取两个参数,预期输出和预测输出,并计算整个数据集的总误差值来定义一个非负误差度量。
![]() ,其中
,其中 ![]() 是一个假设,
是一个假设,![]() 是目标函数。
是目标函数。![]() 基于单个输入
基于单个输入 ![]() 上的误差。因此,我们可以定义一个逐点误差度量
上的误差。因此,我们可以定义一个逐点误差度量 ![]() 。然后,总误差是此逐点误差的平均值。
。然后,总误差是此逐点误差的平均值。![]()
误差度量的选择会影响学习模型的选择。即使数据集和目标函数相同,误差度量的含义也可能因不同问题而异。例如,一个电子邮件垃圾邮件分类器。对于这个电子邮件垃圾邮件问题,学习模型有两种误差结果:误报(false positive)和漏报(false negative)。前者指一封电子邮件是垃圾邮件但学习模型判断它不是;后者指学习模型说一封电子邮件是垃圾邮件,但它不是。想象两种场景:我们的个人电子邮件账户和工作电子邮件账户。
在个人电子邮件账户的情况下,如果学习模型未能过滤掉垃圾邮件,那可能没关系。只是有点烦人。另一方面,如果学习模型过滤掉了一些非垃圾邮件,例如,来自朋友或信用卡公司的邮件。在这种情况下,可能也还好。我们可以使用下表来衡量这种情况。
| 电子邮件是垃圾邮件 | 电子邮件不是垃圾邮件 | |
| 将电子邮件分类为垃圾邮件 | 0 | 1 |
| 将电子邮件分类为非垃圾邮件 | 1 | 0 |
如果学习模型正确分类了一封电子邮件,则此错误的成本为 0。否则,成本为 1。
在另一种情况下:工作电子邮件账户。与个人账户相同,如果学习模型未能过滤掉垃圾邮件,这很烦人但还好。然而,如果学习模型将我们老板的电子邮件分类为垃圾邮件,导致我们错过这些电子邮件,那么这可能就不好了。因此,在这种情况下,漏报的成本比前面的例子更重。
| 电子邮件是垃圾邮件 | 电子邮件不是垃圾邮件 | |
| 将电子邮件分类为垃圾邮件 | 0 | 10 |
| 将电子邮件分类为非垃圾邮件 | 1 | 0 |
再次强调,误差函数(或成本函数、风险函数)确实取决于不同的问题,并且应该由客户定义。
过拟合与欠拟合
“学习是否可行”一节的结论表明,要使学习可行,学习模型必须达到样本内误差小,且样本外误差接近样本内误差。通常,训练集是全局分布的代表,但不可能包含所有可能的元素。因此,在训练模型时,既要努力拟合训练数据,即保持样本内误差小,又要努力使模型在遇到未见过的新输入时能够泛化,即保持样本外误差小。不幸的是,这种理想条件不容易找到,并且需要警惕这两种现象:过拟合和欠拟合。
该图显示了对两类数据的正常分类。

欠拟合意味着学习模型无法捕捉训练数据集中显示的模式。下图展示了欠拟合的情况。

通常,欠拟合很容易被观察到,因为当它发生时,学习模型不能很好地拟合样本内数据。换句话说,当欠拟合发生时,样本内误差很高。
过拟合与欠拟合相反。它意味着学习模型非常好地拟合了训练数据,但拟合得太好以至于无法拟合样本外数据。也就是说,过拟合的学习模型失去了其泛化能力,因此当出现未知输入时,相应的预测误差可能非常高。

与欠拟合不同,过拟合很难被发现或预防,因为过拟合学习模型的样本内误差通常非常低。我们可能会认为我们训练这个模型非常好,直到新数据出现,样本外误差很高。然后我们才意识到模型过拟合了。
过拟合通常发生在学习模型比表示目标函数所需的复杂度更高的情况下。简而言之,过拟合问题可以总结如下:
- 数据点数量增加,过拟合的可能性降低。
- 如果数据集噪声很大,过拟合的可能性很高。
- 模型越复杂,越容易发生过拟合。
学习类型
根据数据类型和我们想解决的问题,我们可以将学习问题大致分为三类:监督学习、无监督学习和强化学习。
监督学习
监督学习可能是研究最充分的学习问题。本质上,在监督学习中,每个样本都包含输入数据和显式输出,即正确输出。换句话说,监督学习可以表示为(输入,正确输出)。
Iris 数据集是一个典型的监督学习案例。该数据集有五个属性作为输入:萼片长度、萼片宽度、花瓣长度、花瓣宽度,以及正确输出,即鸢尾花的类型。我们可以通过绘制 Iris 数据集来可视化监督学习。为了简单起见,我们以萼片长度和花瓣长度作为输入,并使用不同的颜色和符号来表示每个类别,绘制一个二维图。

监督学习的主要目标是从带有正确标签的数据中学习一个模型,以便对未见或未来的数据进行预测。常见的监督学习问题包括:用于预测类别标签的分类和用于预测连续结果的回归,例如垃圾邮件检测、模式检测实例、自然语言处理。
无监督学习
与监督学习相反,无监督学习的数据集不包含正确输出,可以表示为(输入,?)
如果我们不将类型绘制成不同颜色,Iris 数据集就变成了无监督学习的一个例子。
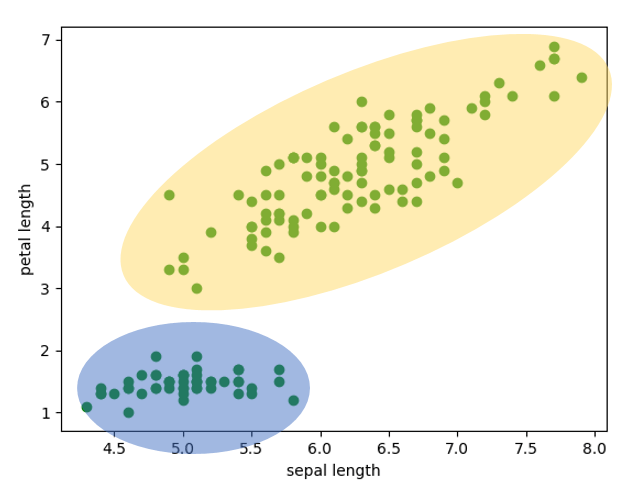
在许多情况下,数据集只有输入,但没有正确的输出,就像上面的图片一样。那么,我们如何从无监督学习问题中学习到一些东西呢?幸运的是,尽管没有正确的输出,但仍有可能从输入中学习到一些东西。例如,在上面的图片中,每个椭圆代表一个簇,其区域内的所有点都可以以相同的方式标记。(当然,我们知道 Iris 数据集有三个类别,这里我们假装我们不知道 Iris 数据集有三个类别)。使用无监督学习技术,我们可以在没有任何先验分组知识的情况下探索数据集的结构以提取有意义的信息。因为无监督学习问题没有标签,所以它处理诸如通过无监督学习发现隐藏结构、通过聚类发现子组以及用于数据压缩的降维等问题。
强化学习
与有输出的监督学习和没有正确输出的无监督学习不同,强化学习的数据集包含输入和某种程度的输出,可以表示为(输入,带分数的某种输出)。
强化学习的一个很好的例子是玩国际象棋和围棋等游戏。下一步的确定是基于当前状态的反馈。一旦做出新一步的决定,就会观察到这一步的等级。强化学习的目标是找出最有用动作的序列,这样强化学习模型就能始终做出最佳决策。
在线 vs. 离线
学习问题也可以通过模型训练方式来区分。
在线学习
数据集一次一个示例地提供给算法。在线学习发生在算法必须“即时”处理流数据的情况下。
离线学习
我们不是一次给算法一个示例,而是在一开始就有大量数据来训练算法。Iris 数据集示例就是离线学习。
在线和离线学习都可以应用于监督学习、无监督学习和强化学习。
机器学习的挑战
随着机器学习(ML)和人工智能(AI)的发展,许多AI/ML驱动的工具和程序在许多领域展现出无限潜力。然而,机器学习并非像许多人想象的那么强大。相反,它有许多显著的弱点,许多研究人员都在积极解决。以下是当今机器学习行业面临的一些挑战。
首先,将学习模型从一个学习问题转移到另一个问题没有简单的方法。作为人类,当我们擅长某件事时,比如下围棋,我们也很可能擅长类似的游戏,比如下国际象棋、打桥牌,或者至少很容易学会这些游戏。不幸的是,对于机器学习来说,即使问题与其他问题相似,它也需要为每个单独的问题重新开始学习过程。例如,我们在上一节中训练的用于分类鸢尾花的感知器学习模型,它能做的就是分类鸢尾花,仅此而已。如果我们想分类不同的花,我们必须从头开始训练一个新的学习模型。
第二个挑战是没有智能的方法来标注数据。机器学习可以做很多事情,可以从各种数据中学习。然而,它不知道如何标注数据。是的,我们可以通过输入大量猫图片来训练一个学习模型来识别动物,比如猫。但是,在一开始,某个人,也就是人类,需要标注这些图片是否是猫图片。即使无监督学习可以帮助我们对数据进行分组,它仍然不知道一组图片是否是猫。如今,标注数据仍然需要人类的参与。
第三,即使是机器学习解决方案的创建者也不知道为什么机器学习解决方案会做出这个决定。机器学习的本质是从数据中学习。我们向学习模型输入数据,它预测结果。在感知器学习算法示例中,最终假设的权重可能看起来像 [-4.0, -8.6, 14.2],但很难解释为什么学习模型会给我们这些权重。即使是最简单的学习算法,感知器,我们也无法解释为什么。更不用说,几乎不可能解释更复杂的学习算法是如何工作的。这个问题可能导致严重的后果。特别是对于错误成本高的学习问题,例如自动驾驶汽车,如果事情出错而我们不知道它是如何出错的,我们又如何修复它呢?
这三个挑战仅仅是冰山一角。尽管机器学习似乎拥有无限潜力,但它仍然有很长的路要走。
