Vogel 螺旋现象。

• 下载完整的项目源代码 - 8 Kb

引言

看起来螺旋有无限多样的种类[1-11]。但有时，螺旋并不像我们预期的那样，特别是许多 Vogel 螺旋，以及多螺旋线和许多特殊类型的螺旋，例如，Ulam 螺旋、螺旋矩阵等。

注意：H. Vogel 在 [5, p.182] 中将他的螺旋称为其他名称：“为了缺乏更好的术语，我们将螺旋……称为旋涡螺旋。”

这里有一个来自维基百科[1]的关于一般螺旋项的简单定义

这里是来自 RosettaCode Wiki [2] 的另一个方便的定义

本文的目的是证明螺旋图像可能非常棘手和令人困惑，根本不像螺旋。但这种外观是真实的，并且将解释为什么会发生这种现象。

不清楚“完全数学构造程序”[5]是什么？但在 [5-7] 中，计算机肯定被用于计算和显示螺旋。

此外，要考虑到那个时代计算机不同且速度慢。正如 H. Vogel 在 [5] 中解释的那样：“所有图形都是从 PDP-12 屏幕拍摄的。”看起来他们使用的是一种看起来像大点的 ASCII 符号，因为他们没有用线条绘制的软件。

在 [7] 中提到 T.A. Davis 曾借助一位艺术家，所以，螺旋在某些情况下是“构造”并手动绘制的。

关于 Vogel 螺旋

许多文章 [5-8] 以及 [5] 之后的更多文章都致力于一些有趣且引人入胜的图案现象。这一切始于多年前对向日葵和雏菊花头[8]上发现的图案的初步研究，并且从未停止过。

在 [7] 中提出了所谓的“黄金角度”，也称为“斐波那契角度”

在 [5, p. 180] 中提出了以下公式（现在“翻译”成我们的表示法）

在 [5] 中可以找到一些对我们来说更重要的其他要点（此处强调）

所有这些词“近似”、“不规则性”和“有争议”都告诉我们犹豫不决。他们正在寻找精确的解决方案，但他们是在向日葵头部寻找，而不是在螺旋中寻找。顺便说一句，他们称之为旋涡螺旋。也许是为了将其与常规的“可见”螺旋区分开？这是相当正确的：他们构建的东西根本不像螺旋！无论如何，现在这种螺旋被称为 Vogel 螺旋。

以下 JavaScript 代码片段展示了任何 Vogel 螺旋的生成和绘制过程，包括设置选定的绘图样式，即使用点或线进行绘制。

  // setting ctx styles: colors, plotting units (dots/lines)
  // canvas size - cw x cw; canvas center - cc; scale - sc.
  ctx.fillStyle="white"; ctx.fillRect(0,0,cw,cw); // cleaning canvas
  if(pu=="d") {ctx.fillStyle=clr; } // pu - plotting unit ("d"-dot, "l"-line)
  else {ctx.strokeStyle=clr; ctx.beginPath(); ctx.moveTo(cc, cc);} // Lines
  // Prime loop: generating/plotting Vogel spiral
  for(var i=0; i<n; i++) {
    // Calculating polar coordinates theta (t) and radius (r)
	t=it*i; r=Math.sqrt(i/n);
    // Converting to the Cartesian coordinates x, y
    x = sc*r*Math.cos(t) + cc; y = sc*r*Math.sin(t) + cc;
    if(pu=="d") {bDot(x,y,5)} // Dots
    else {ctx.lineTo(x, y);}  // Lines
  }//fend i
  if(pu=="l") {ctx.stroke()}  // Lines

正如你所见，它相当简单，只有 10 行代码（在典型的绘制螺旋的初始循环中）。

在许多情况下，生成任何螺旋的循环具有相同的结构（如上所示），这反映了使用极坐标系 [1,3] 更适合任何螺旋的事实。因此，在极坐标系中，大多数具有唯一方程/函数的螺旋（和其他图形）如下：r = f(theta)，其中半径 r 是角度 theta 的单调连续函数。

极坐标 r 和 theta 可以按以下方式转换为笛卡尔坐标 x 和 y [3]：x=r*cos(theta) 和 y=r*sin(theta)。
注意：在上面的片段中，t 被用作 theta。

只有 2 个基本系数用于更改螺旋的“外观和感觉”：it - 初始角度 theta 和 n - 点的数量。所有其他都是常量，例如画布尺寸、比例等。但玩弄它们也很有趣。

注意：[图 1a] 中的第一个螺旋是最著名的。这里将其称为“标准”Vogel 螺旋。所有其他用点绘制的图形都部分受到 [6,10] 的启发。

在下面的图形中，您可以自己查看所有这些图形，其中每个图形 Na（用点绘制）和 Nb（用线绘制）都有 3 个螺旋，使用相同的初始角度 it 和相同的点数 n 进行绘制。

此外，为了清楚地展示我们的观点，Nb 图形中的第二个和第三个螺旋都使用点和线进行绘制（例如，参见 [图 1b/2-3]）。

上面 [图 1a] 中的第一个螺旋是标准 Vogel 螺旋。有时也称为“向日葵种子/小花”。
关于 [图 1a] 的简要说明

• 标准 Vogel 螺旋有许多可见的顺时针和逆时针次螺旋臂。但它是螺旋吗？
• 第二个螺旋没有任何明显的图案，仍然不像螺旋。我曾怀疑某个角度是否会是“黄金”的。但在这一点上，我不再那么确定了……尽管如此，如果点数很少，即使是“黄金”角度也无济于事。例如，[图 1a/2,3]
• 第三个螺旋有一些次螺旋臂，仍然不像螺旋。

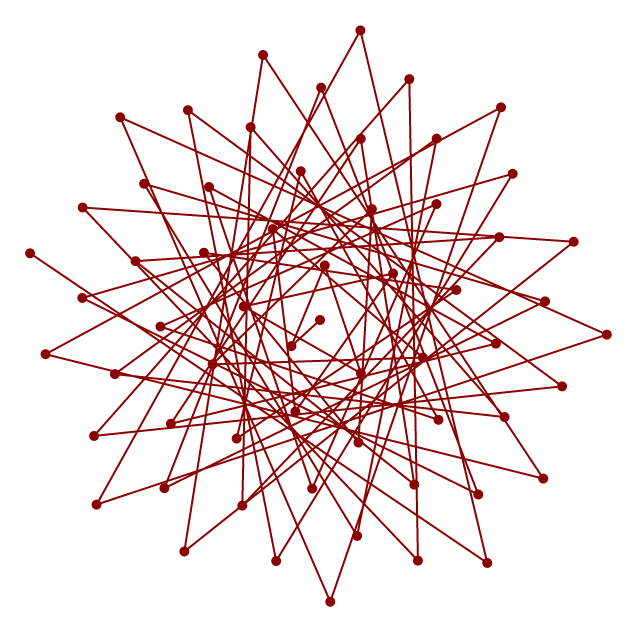
如果将 2 个连续生成的点用线段连接起来，图片就会不同，即螺旋是用线绘制的。

关于 [图 1b] 的简要说明

• 第一个螺旋现在看起来像向日葵的头部。很难相信它是一个螺旋。
• 第二个螺旋绝对是一个螺旋！终于！但它看起来更像一个多螺旋线，线段重叠。
• 仅从第三个螺旋的中心区域来看，就可以看出：这是一个多螺旋线！反过来，这也证明了第一个螺旋也是一个多螺旋线。

• 任何看到用大点绘制的 Vogel 螺旋（在 Na/1 图中）的人都看不到任何螺旋。我们都不是错觉！我们只是视力取决于我们的大脑，而后者向我们提供了顺时针和逆时针的次螺旋臂。它们是真实的。要证明这一点——只需打印第一张图片，并用彩色笔连接手臂中的点。
• 图 Na 中的所有螺旋都是肯定的螺旋，只是螺旋性对观察者隐藏了。Nb 图为我们提供了证据。

我的朋友（他是一名音乐家）问我：“你为什么坚持认为第二个螺旋（在 [图 1b] 中）是一个螺旋？请向我解释！我看到线和点，但没有任何螺旋？！”我尝试了几种“理由”，但都没有奏效。直到我说：“因为这条曲线从画布中心开始，并且明显地围绕中心点盘旋，而且它总是使线圈变大。”他感到满意。
 

关于 [图 2a] 的简要说明

• 中心区域的第一个螺旋看起来像螺旋。但随后它向我们展示了很多顺时针螺旋臂。
• 第二张和第三张图片是单个螺旋臂。

关于 [图 2b] 的简要说明

• 非常清楚，第一个螺旋是一个从中心开始的真正的螺旋。此外，这是一个非常光滑的螺旋，尽管它仍然是一个多螺旋线。没有可见的线段或次螺旋臂。
• 应该强调的是，任何用线绘制的螺旋都是多螺旋线。如果绘图角度很小，那么螺旋看起来就很光滑。有时，螺旋在靠近中心的地方看起来很光滑，但靠近画布边界时，线段会变得可见。
• 第二张和第三张图片是单个螺旋臂。

关于 [图 3a] 的简要说明

• 所有 3 个螺旋都不像螺旋。中心区域的第一个螺旋看起来有 9 个螺旋臂。但随后它向我们展示了很多顺时针螺旋臂。
• 第二张和第三张图片看起来有许多单螺旋臂。

关于 [图 3b] 的简要说明

• 非常清楚，所有 3 个螺旋都是从中心开始的真正的多螺旋线。
• 第三张图片展示了螺旋臂是如何绘制的，这反过来解释了为什么我们会看到它们：螺旋臂中点之间的距离远小于多螺旋线中相关线段的长度。所以，我们的大脑告诉我们：“嘿，看——这是 9 个螺旋臂（在 [图 3a/3] 中）！”而我们会同意。

[图 4a] 与 [图 3a] 类似，但所有螺旋臂的方向相反，即逆时针。

现在非常清楚，[图 4b] 中的所有 3 个螺旋都是从中心开始的真正的多螺旋线。

[图 5a] 与 [图 3a] 类似，但中心区域除外。

非常清楚，[图 5b] 中的所有 3 个螺旋都是从中心开始的真正的多螺旋线。

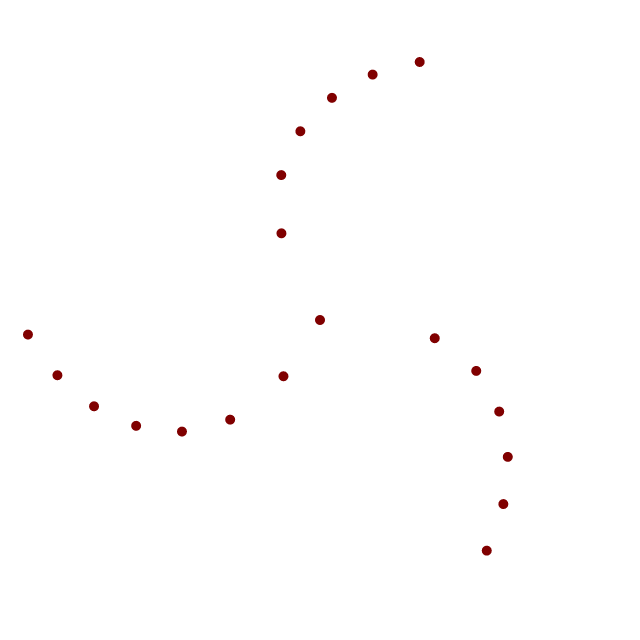
关于 [图 6a] 的简要说明

• 你注意到这里的第一个螺旋与标准 Vogel 螺旋 [图 1a/1] 有非常相似的图案吗？也就是说，它有很多可见的顺时针和逆时针次螺旋臂，但在中心区域没有密集的种子。
• 我认为它更精确地匹配了真实的自然向日葵种子图案。特别是，因为真实的向日葵中心区域没有种子。你怎么看？
  我只是在嘲弄这个主题的真正专家，因为我离进行这种植物学分析还远着呢。

非常清楚，[图 6b] 中的第二个和第三个螺旋都是从中心开始的真正的多螺旋线。如果是这样，那么第一个螺旋也是一个多螺旋线。

此外，第三个螺旋向你展示了次螺旋臂是如何由重叠的线段形成的。

使用示例网页

zip 文件中附带了几个网页：“VogelSpiral”、“VogelSpiral2”和“VogelSpiral3”。前两个页面使用默认参数集。

第一个页面生成并绘制点或线绘制的 Vogel 螺旋（参见 [图 1a,b - 图 6a,b] 的结果）。

第二个页面使用点和线绘制螺旋（参见 [图 1b - 图 6b] 的结果）。

第三个页面是 [11] 中“螺旋生成器”页面的修改版本。它允许用户查看使用不同初始角度绘制的 Vogel 螺旋有多接近。这是可能的，因为它允许使用不同的颜色将一个螺旋绘制在另一个螺旋之上。

如果您想查看 Vogel 螺旋的完整范围，可以使用“VogelSpiral3”。在下面的表 1 中查找已测试的样本。先尝试它们。然后找到您自己喜欢的样本。

关于表 1 的注释

• 初始角度 'it' 在第二列显示起始初始角度 it。
• 比例 在第四列显示附加的缩放参数，允许用户加速测试非常大的初始角度 it。例如，样本 #2 的初始角度大于 41K 度。
• P/O 显示绘图模式：“P”代表初始绘图（清除画布）；“O”代表在已绘制螺旋上进行绘图。

表 1. 测试样本

#	初始角度 'it'	点	Scale	Color	P/O	注释
1	0.1	256	1.0	深绿色	P	平滑螺旋
2	7.138	256	103.0	深绿色	P	再次纯螺旋
3	2.399963	256	1.0	深绿色	P	标准 Vogel 螺旋
4	2.4	256	1.0	red	O	几乎相同 [给 'it' 添加了 0.0001]
5	2.401	256	1.0	黄色	O	几乎相同 [给 'it' 添加了 0.001]
6	2.5	256	1.0	海军蓝	P	不同的图案
7	7.13	256	1.0	海军蓝	P	相同的图案
8	7.134	256	1.0	海军蓝	P	相同的图案
9	7.135	256	1.0	海军蓝	P	相同的图案
10	7.136	256	1.0	海军蓝	P	相同的图案
11	2.399963	256	2.0	栗色	P	相同的图案
12	2.399963	256	3.0	栗色	P	相同的图案
13	2.6	256	1.0	red	P	相同的图案
14	2.7	256	1.0	red	P	不同的图案
15	2.9	256	1.0	red	P	不同的图案
16	3.0	256	1.0	red	P	相同的图案
17	3.3	256	1.0	red	P	相同的图案
18	3.4	256	1.0	red	P	相同的图案
19	5.3	256	1.0	red	O	相同的图案

如果您继续测试，很快就会发现成千上万种外观不同（和相似）的螺旋。

• 将初始“黄金”角度（无理数，深绿色点）改变 +0.0001 弧度（现在是有理数，红色点）几乎没有影响最终的螺旋。实际上，如果颜色相同，肉眼无法检测到差异。在 [图 7] 中，您可以看到重叠的深绿色和红色点主要靠近画布边缘。
• 将初始角度（有理数，黄色点）增加额外的 0.001 会稍微改变这个螺旋。但这个螺旋仍然具有几乎相同的图案，即许多可见的顺时针和逆时针次螺旋臂。
• 表 1 中的许多其他样本（#7-#19）也产生接近标准 Vogel 螺旋的图案。
• 此外，尝试改变点的数量以查看不同的图案。这是由于画布绘图中使用的默认比例。
• #6：不同的图案，只有逆时针臂是显著的；
• #7：相同的图案，但顺时针臂更显著；
• #8-#10：相同的图案，但逆时针臂越来越显著；
• #11：实际上，仍然是相同的图案，但逆时针臂更显著；
• #12：几乎相同的图案，但顺时针臂更显著；
• #13：几乎相同的图案，但逆时针臂在中心区域更显著；
• #14：不同的图案，只有顺时针臂是显著的；
• #15：不同的图案，只有逆时针臂是显著的（在中心区域）；
• #16：几乎相同的图案，但逆时针臂在中心区域更显著，加上一个不同的中心；
• #17：几乎与 #15 相同。
• #18：几乎与 #16 相同。
• #19：几乎与 #3 相同，只需在 #3 之后绘制即可。尝试 it=1.7 进行比较
• 也尝试以下 it：0.2、0.5、1.0、1.1、1.2、1.5、1.9、2.0、2.23、2.27、2.3。等等……

结论

[6,10] 及其他几篇文章的作者讨论了选择初始角度是整数还是无理数？

实际上，有理数和无理数之间的差异非常小。因此，关于角度必须是无理数的说法是不正确的。事实上，许多有理数可以产生相同的图案，至少与标准 Vogel 螺旋非常接近（见下文 [图 7]）。

[图 7] 使用“Vogel3”页面和表 1 样本：#3、#4 和 #5 进行绘制。现在非常清楚了。

• 将初始“黄金”角度（无理数，深绿色点）改变 +0.0001 弧度（现在是有理数，红色点）几乎没有影响最终螺旋。实际上，如果颜色相同，肉眼无法检测到差异。在 [图 7] 中，您可以看到重叠的深绿色和红色点主要靠近画布边缘。
• 将初始角度（有理数，黄色点）增加额外的 0.001 会稍微改变 Vogel 螺旋。但螺旋仍然具有几乎相同的图案，即许多可见的顺时针和逆时针次螺旋臂。
• 表 1 中的许多其他样本（#7-#19）也产生接近标准 Vogel 螺旋的图案。

嗯……也许 137.507 度的角度在这种情况下不是那么“黄金”？！

• 首先，[图 1a] 中的起始“标准”Vogel 螺旋非常流行，并且在 [5-7]（以及许多其他文章）中都有介绍，但作者尚未将其与使用非常大的黄金角度和绘制大点这一幸运巧合联系起来。我们感谢 H. Vogel 发现了这种惊人的图案。如果他和他的同行使用线条进行绘制（即使使用黄金角度），他们也永远不会看到这种图案。作者一直在研究向日葵的种子图案，因此，合乎逻辑的选择是使用大点。这很有帮助。
• 其次，生产所需图案最重要的是 H. Vogel 为头状花序定义的以下单位和参数集：
  • 大点（不是线段）；
  • 一个大的初始角度和一个递增方法（小角度会产生平滑的螺旋，即使使用更大的角度也有效，例如，参见 [图 6a/1]）；
  • 点的数量（少量点不会产生所需的图案，但大量的点可以做到，例如，参见 [图 6a/1]）；
  • 独特的函数，即 Vogel 函数。

应该强调的是，在 [9] 中提到了以下内容

这是正确的观点，但下一个观点只是部分正确 [9]

注意：他们谈论的是真实的、可见的次螺旋臂。

说“实际上没有这样的螺旋”是错误的。螺旋（螺旋臂）就在那里！它们是真实的！你可以手动绘制它们。正确的是陈述的其余部分，即“是人的视觉创造了径向螺旋。”但这只在知道整个图像是一个螺旋的上下文中才是正确的。

所以，他们仍然没有将这种可见的图案与使用黄金角度和绘制大点这一幸运巧合联系起来。

我认为，如果有人能告诉我们为什么某个角度会欺骗我们的视觉和大脑，那将非常有趣。我的意思是，指向比我的解释更精确的解释，如果有的话。

也许，当我们看到螺旋星系的图片时，我们也被欺骗了？也就是说：我们看到的不是数十亿围绕黑洞旋转的恒星，而是这些恒星排列成螺旋臂的图片。原因相同：我们看不到椭圆轨道，因为它们之间的距离很小，而且每个恒星都有自己的轨道。相反，我们得到的是所有恒星看起来像螺旋臂的快照。注意：并非所有星系都有螺旋臂。它们中的大多数看起来像圆盘，这可能支持这个假设。

参考文献

1. 螺旋，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/Spiral。
2. 多螺旋线，Rosetta Code Wiki，网址：http://rosettacode.org/wiki/Polyspiral。
3. 极坐标系，维基百科，自由的百科全书，网址：https://en.wikipedia.org/wiki/Polar_coordinate_system。
4. Wassenaar, J. Mathematical curves, 网址：http://www.2dcurves.com/spiral/spiral.html
5. Vogel, H (1979). A better way to construct the sunflower head. Mathematical Biosciences. 44 (44): pp. 179-189. doi:10.1016/0025-5564(79)90080-4。
6. Prusinkiewicz, P.; Lindenmayer, A (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101-107. ISBN 978-0-387-97297-8。
7. Mathai, A.M.; Davis, T.A. (1974) Constructing the sunflower head, Mathematical Biosciences, 20, 117-133. doi: 10.1016/0025-5564(74)90072-8。
8. Bonnet, C.(1754) Recherches sur I’usage des feuilies akns les p/antes, Gottingen and Leiden。
9. Haubold, H.J; Mathai, A.M. (2015) Scientific Endeavors of A.M. Mathai: An Appraisal on the Occasion of his Eightieth Birthday. 网址：https://arxiv.org/pdf/1502.07382.pdf
10. Devert, A. Spreading points on a disc and on a sphere. 网址：http://blog.marmakoide.org/?p=1。
11. Voevudko, A.E. (2017) Dancing with Spirals. Code Project, 网址：https://codeproject.org.cn/Articles/1213518/Dancing-with-Spirals。

历史

2017/12/17 根据朋友的请求更新“结论”。添加“历史”。以及一些简短的编辑。
2017/12/15 初始发布。