从零开始的 3D 计算机图形学
在几乎没有数学知识的情况下,
引言
介绍3D图形学的一个起点是深入研究其历史渊源,几何学的基础是在古希腊时期奠定的,其中泰勒斯、毕达哥拉斯和欧几里得等人物做出了重大贡献,欧几里得通常被誉为“几何学之父”。
- “几何学”(Geometry)一词源于古希腊语
γεωμετρία(geometria),由两个元素组成:
- Γῆ (Ge): 这个元素意为“大地”
- Μέτρον (Metron): 这个元素意为“测量”或“度量”
当这两个词组合在一起时,γεωμετρία 一词意为研究由实际测量定义的空间关系,分析和描述地球土地的特征,用于农业、建筑和导航等实际应用。
欧几里得写了一本名为《几何原本》的书,其中他为几个基本的几何术语提供了具体的定义:
- «
Σημεῖόν ἐστιν, οὗ μέρος οὐθέν» 可以翻译为 “点是不可再分的部分”,这个定义强调了点的几何不可分割性,因此其唯一可测量的属性是两点之间的距离。 - «
Γραμμὴ δὲ μῆκος ἀπλατές» “线有长度而无宽度”,强调了线只有一个可测量的属性,即其长度。 - «
Γραμμῆς δὲ πέρατα σημεῖα» “线的末端是点”,这表明线是由点组成的,因为线可以有不同的长度。 - «
Σῶμά ἐστι τὸ μῆκος, πλάτος, βάθος ἔχον» “立体是有长度、宽度和深度的”,意味着一个立体有3个互不重叠的可测量属性。 - «
Τριγώνου δεξιοῦ τὸ τετράγωνον τῆς ὑποτείνουσης τοὺς τετραγώνους τῶν περὶ τὰς ἄλλας πλευρὰς ἰσότητα πεποιήκαμεν» “在直角三角形中,斜边上的正方形等于另外两条边上的正方形之和”,我们将在后面保留这个命题来解释旋转空间变换。
有了这些概念,我们就可以仅用点来构建任何几何元素。
因此,我不依赖现代3D图形技术来渲染几何元素,而是依据欧几里得在他的《几何原本》一书中所设定的点的定义。
引言
欧几里得没有引入我们所熟知的笛卡尔坐标系中的轴、坐标和维度空间等概念,但对点和线的全面分析可以为其奠定基础。
欧几里得的论述“Γραμμῆς δὲ πέρατα σημεῖα”也强调了线段两个端点之间的空间关系,即它们之间的相对空间位置,而长度则说明了该位置。
因此,如果点之间存在空间关系,并且任何几何元素都可以由点构成,那么几何元素内的每个点都拥有相对于该元素的唯一空间位置。
为了精确确定一个点在比线更复杂的几何元素内的相对空间位置,我们可以从这个点到每个现有或假想的测量线内的另一个点画出最短的线,从而建立一个相互连接的点的网络,这个网络定义了它们的相对空间位置。
而用一组点来构建任何几何元素的最佳选择是 στερεὰ (sterea),即一个几何立体,例如 παραλληλεπίπεδον (平行六面体),因为它的线条勾勒出了长度、宽度和深度,且互不重叠,因此 παραλληλεπίπεδον 内的每个点都将有一组3个测量值/距离,分别对应它与 παραλληλεπίπεδον 的长、宽、深三条线上的对应点之间的距离。
后来,这些测量分量被称为坐标,是相对于测量线的坐标,这些测量线将被称为轴,每个轴都开辟一个维度空间。
在古希腊,测量通常基于几何和比例关系,而不是像我们今天这样有标准化的单位,因此 πῆχυς (腕尺) 和 στάδιον (斯塔德) 被用作计数单位来设定建筑中的距离。
欧几里得有一把 Κανών (尺子) 用来绘制他的几何元素,上面没有数值标记,一个 πῆχυς 的长度不适合用来绘制几何元素,因此在19世纪末出现的公制系统成为了最佳的测量单位选择。
现在我们已经奠定了笛卡尔坐标系的基础,我们还有一项研究需要完成。虽然我们可以通过给一个点的3个测量分量之一加上一个变量来逻辑上地在直线上移动它,但我们还剩下一种空间变换,即在曲线上移动一个点,这被称为旋转。
而圆是旋转的完美几何候选者,因为它内部的所有点都以其中心的一个参考点为基准,视觉上围绕着该参考点旋转。
正如欧几里得上面所述,“在直角三角形中,斜边上的正方形等于另外两条边上的正方形之和”,这强调了直角三角形三条边长之间存在着一种空间关系,即我们所熟知的勾股定理。
HypotenuseLength × HypotenuseLength = FirstSideLength × FirstSideLength + SecondSideLength × SecondSideLength
虽然我们可以用这种方式来旋转点,但由于缺乏一种称为角度的旋转度量,旋转点时会不够精确。
不幸的是,我没有找到连接勾股定理和三角函数之间的桥梁,后者使用角度而不是直角三角形的属性来画圆。因此,对欧几里得著作的全面分析到此为止,我们必须跨越到现代几何时代。
三角函数如 sin(θ) 和 cos(θ),其中 θ 代表圆上的一点相对于圆的X测量线的角度,并返回该点相对于其测量线的相应位置。
这些测量线通常被称为X轴和Y轴。

因此,我们将从对三角圆的视觉研究开始,以实现点的旋转。
首先,我们设置一个点在 0° (x = 1, y = 0),然后我们将这个点围绕中心旋转 +90°(+代表逆时针,-代表顺时针),要找到的结果是 x = 0, y = 1。
而找到这个结果的通用公式是:
X′ = X × cos(θ) - Y × sin(θ)
Y′ = X × sin(θ) + Y × cos(θ)
从零开始推导出这个方程相对简单,稍后我们将看到,这些公式只是Z轴旋转矩阵的线性形式。
方法如下:
- 我们有一个半径为4的圆,它有两条测量线(即2D)。
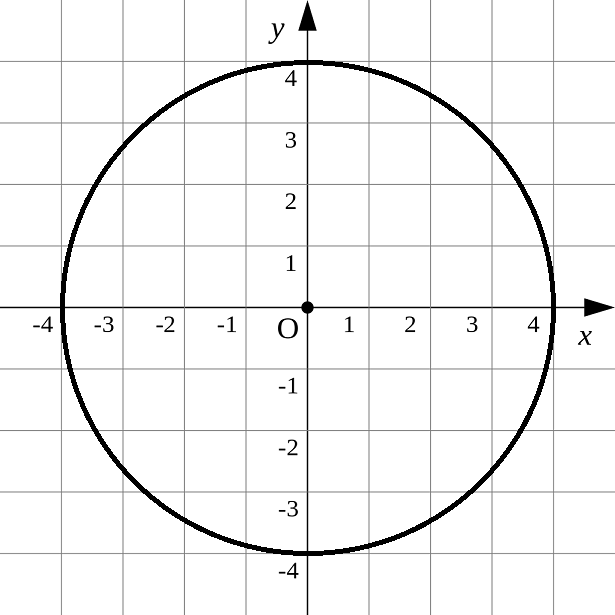
- 我们设置一个点,旋转它,并试图找出导致其新位置的方程。因此,一旦我们对 P(X, 0) 和 P(0, Y) 的组合进行操作,我们就能找到旋转任何 P(X, Y) 的方程。
- 让我们从P(4, 0)开始,视觉上是一个红点。

- 我们将这个点旋转+90°,并试图找到其新位置的方程,视觉上要找到的结果是P(0, 4)。

X = sin(θ) = 1 ❌ X = cos(θ) = 0 ✔ Y = cos(θ) = 0 ❌ Y = sin(θ) = 1 ❌✔ Y = 4 × sin(θ) = 4 ✔
- 所以对于 P(4, 0) 且 θ = 90°,我们有:
X′ = cos(θ) Y′ = X × sin(θ)
- 尝试用其他角度对 P(4, 0) 进行计算,会得到一些略有不同的方程(使用 mathsisfun),但将它们组合起来,会得到这个结果:
-
X′ = 4 × cos(θ) = X × cos(θ) Y′ = 4 × sin(θ) = X × sin(θ)
- 现在我们将红点设置在 P(0, 4)。

- 我们将这个点旋转+90°,视觉上的结果是 P(-4, 0)。

X = cos(θ) = 0 ❌ X = sin(θ) = 1 ❌✔ X = 4 × -sin(θ) = -4 ✔ Y = sin(θ) = 1 ❌ Y = cos(θ) = 0 ✔
- 所以对于 P(0, 4) 且 θ = 90°,我们有:
X′ = Y × -sin(θ) Y′ = cos(θ)
- 尝试用其他角度对 P(0, 4) 进行计算,会得到一些略有不同的方程,但将它们组合起来,会得到这个结果:
X′ = 4 × -sin(θ) = Y × -sin(θ) Y′ = 4 × cos(θ) = Y × cos(θ)
- 现在让我们总结一下:
_________________ _________________ | | | | P(X, 0) | P(0, Y) | |_________________|_________________| | | | | X′ = X × cos(θ) | X′ = Y × -sin(θ)| | Y′ = X × sin(θ) | Y′ = Y × cos(θ)| |_________________|_________________|
正如我们所见,当X或Y等于0时,会产生不同的方程。让我们看看当X和Y的值小于4且大于0时会发生什么。
- 因此,我们将点设置在 P(2, 4×√3/2)。

- 现在我们将这个点旋转+30°,视觉上要找到的结果是 P(0, 4)。

X = sin(θ) = 0.5 ❌ X = cos(θ) = √3/2 ❌ Y = sin(θ) = 0.5 ❌ Y = cos(θ) = √3/2 ❌
我们遇到了一个问题,没有任何一个三角函数能起作用,所以我们需要从别处寻找解决方案。
让我们回顾一下之前找到的方程:
_________________ _________________ | | | | P(X, 0) | P(0, Y) | |_________________|_________________| | | | | X′ = X × cos(θ) | X′ = Y × -sin(θ)| | Y′ = X × sin(θ) | Y′ = Y × cos(θ)| |_________________|_________________|
如果X和Y都大于0,会发生什么?它应该是两者的混合体。
X′ = X × cos(θ) X′ = Y × -sin(θ)
Y′ = X × sin(θ) Y′ = Y × cos(θ)
X′ = X × cos(θ) Y × -sin(θ)
Y′ = X × sin(θ) Y × cos(θ)
让我们看看相加是否可行:
X′ = X × cos(θ) + Y × -sin(θ)
X × cos(θ) - Y × sin(θ)
Y′ = X × sin(θ) + Y × cos(θ)
X′ = 2 × cos(θ) - 4×√3/2 × sin(θ) = 0 ✔
Y′ = 2 × sin(θ) + 4×√3/2 × cos(θ) = 4 ✔
完美,这个方程给出了正确的结果。所以,最终在XY平面上的最终方程是:
X′ = X × cos(θ) - Y × sin(θ)
Y′ = X × sin(θ) + Y × cos(θ)
为了结束这次视觉研究,让我们用 P(X, 0) 和 P(0, Y) 来试试。
- 对 P(4, 0) 进行+90°的旋转,视觉上要找到的结果是 P(0, 4)。
X′ = 4 × cos(θ) - 0 × sin(θ) = 0 ✔ Y′ = 4 × sin(θ) + 0 × cos(θ) = 4 ✔
- 对 P(0, 4) 进行+90°的旋转,视觉上要找到的结果是 P(-4, 0)。
X′ = 0 × cos(θ) - 4 × sin(θ) = -4 ✔ Y′ = 0 × sin(θ) + 4 × cos(θ) = 0 ✔
既然我们已经从零开始推导出了在XY圆上旋转一个点P(X, Y)的通用公式,我们就可以开始研究旋转矩阵了。
-
如前所述,这个公式只是Z轴旋转矩阵(XZ平面旋转矩阵)的线性形式,乘以点的测量分量,也称为向量。
Rotation matrix on z: Vector: _______________ _______________ _______________ _______________ | | | | | | | cos(θz) | -sin(θz) | 0 | | x | |_______________|_______________|_______________| |_______________| | | | | | | | sin(θz) | cos(θz) | 0 | × | y | |_______________|_______________|_______________| |_______________| | | | | | | | 0 | 0 | 1 | | z | |_______________|_______________|_______________| |_______________|
一个3D坐标系可以由几个2D坐标系来描述,每个平面都在3D坐标系中的任何地方驱动着旋转空间变换。
因此,我们需要收集所有构成3D坐标系的2D旋转矩阵,共有3个:
X轴旋转矩阵(XY平面旋转矩阵)
_______________ _______________ _______________
| | | |
| 1 | 0 | 0 |
|_______________|_______________|_______________|
| | | |
| 0 | cos(θx) | -sin(θx) |
|_______________|_______________|_______________|
| | | |
| 0 | sin(θx) | cos(θx) |
|_______________|_______________|_______________|
Y轴旋转矩阵(YZ平面旋转矩阵)
_______________ _______________ _______________
| | | |
| cos(θy) | 0 | -sin(θy) |
|_______________|_______________|_______________|
| | | |
| 0 | 1 | 0 |
|_______________|_______________|_______________|
| | | |
| sin(θy) | 0 | cos(θy) |
|_______________|_______________|_______________|
Z轴旋转矩阵(XZ平面旋转矩阵)
_______________ _______________ _______________
| | | |
| cos(θz) | -sin(θz) | 0 |
|_______________|_______________|_______________|
| | | |
| sin(θz) | cos(θz) | 0 |
|_______________|_______________|_______________|
| | | |
| 0 | 0 | 1 |
|_______________|_______________|_______________|
最后,为了在3D坐标系中实现对欧几里得点的旋转,我们需要将上述2D旋转矩阵相乘,并且乘法的顺序很重要,但我们将在下一篇教程中更详细地探讨这一点。
历史
- 2024年2月1日:文章/代码更新,从欧几里得的著作开始解释计算机图形学。
- 2018年6月12日:初始版本
