WPF 3D 中的裁剪平面 - 第 3 部分

• 下载源代码 - 244.5 KB

引言

在WPF 3D 中的裁剪平面，第 2 部分中，我演示了有限裁剪平面如何“切割”模型，使用一种算法来确定给定点的投影是否位于由两个三角形定义的平面内，从而移除裁剪平面一侧的片段。在本第 3 部分中，我将演示如何围绕海绵自身的轴旋转它，并沿着世界坐标系平移它。

背景

我假设读者已经阅读了之前关于 WPF 的文章，并且对矩阵代数有所了解。

Using the Code

下载并构建

下载 MengerSpongeClipping.zip 测试文件并解压缩。使用 Visual Studio 打开 MengerSpongeClipping 项目。它包含两个项目：MengerSpongeClipping WPF 应用程序和 Microsoft 3DTools 库。按 F6 构建它；项目应该成功构建，没有错误。按 F5 以调试模式运行 MengerSpongeClipping 项目。

世界坐标系和局部坐标系

“世界坐标系”一词指的是场景的主笛卡尔坐标系。在第 2 部分中，我展示了背景框（使用 B 键切换开/关）如何表示世界坐标系，其中 X 轴指向南方，Z 轴指向西方，Y 轴指向上方。

海绵（或我之后将称之为立方体）有其自己的局部坐标系，其 XYZ 轴的原点位于中心，最初与世界坐标系对齐。通常，三维空间中的旋转是不可交换的。为了演示，下面的第一张图片显示了立方体先绕其 X 轴旋转 90 度，然后绕其 Y 轴旋转 90 度，最后绕其 Z 轴旋转 90 度后的状态。请注意立方体的 X 轴如何指向西方（世界 Z 轴），立方体的 Y 轴指向下方，立方体的 Z 轴指向南方（世界 X 轴）。第二张图片显示了立方体先绕其 Z 轴旋转 90 度，然后绕其 Y 轴旋转 90 度，最后绕其 X 轴旋转 90 度后的状态。旋转的量和轴与第一张图片相同，但顺序不同，因此结果也不同。在第二种情况下，立方体的 X 轴指向东方（世界 -Z 轴），立方体的 Y 轴指向上方。（立方体的 Z 轴保持指向南方。）

在我深入讨论旋转和平移代码的细节之前，我首先想谈谈版本 2 的外观和其他更改。

版本 3 的新功能

在我看来，布局变得过于“头重脚轻”，控件都在顶部，所以我将其更改为水平布局，控件在左侧，3D 视口在右侧。这展示了 WPF 的 <Grid> 容器的使用，3D 视口位于最右边的列并跨越所有行，通过设置 Grid.RowSpan="12"。当前的变换矩阵现在显示在左侧。我还为立方体添加了面标签，以便更容易看到旋转的结果。

您可以围绕立方体自身的轴旋转它，并且可以沿着世界坐标系轴平移它。旋转和平移的量是可配置的。我最初可以选择使用滑块或键盘进行旋转，但保持两者同步使得代码难以维护，而且我发现键盘提供了更精确的控制，所以我最终移除了滑块。版本 3 中用于旋转和平移的新键和按钮是

1. 使用 X、Y、Z 分别围绕立方体的 X、Y 和 Z 轴旋转立方体，旋转量由 app.config 文件中的 SpongeRotateIncrement 指定。默认的 SpongeRotateIncrement 为 15 度，因此按 X 键六次将使立方体绕其 X 轴旋转 90 度。
2. Shift X、Y、Z 将使立方体沿负方向旋转 SpongeRotateIncrement 度。
3. Ctrl-Z 将撤销上次旋转。
4. 有两种平移，粗略平移和精细平移。
5. 要在世界坐标系中平移立方体，平移量由 app.config 中的 SpongeTranslateIncrementCoarse 指定，请使用 J、K 和 L 分别沿正 X、Y 和 Z 轴平移它。默认的 SpongeTranslateIncrementCoarse 是 4.0，因此按 J 键 2 次将使立方体在 X 方向（南方）平移 8 个单位。
6. 使用 Shift J、K 和 L 沿负 X、Y 和 Z 轴平移立方体。
7. 要按 app.config 中指定的 SpongeTranslateIncrementFine 量平移立方体，请使用 Ctrl J、K 和 L 分别沿正 X、Y 和 Z 轴平移它。默认的 SpongeTranslateIncrementFine 是 0.5，因此按 Ctrl-L 键 3 次将使立方体在 Z 方向平移 1.5 个单位。
8. 使用 Ctrl-Shift J、K 和 L 沿负 X、Y 和 Z 轴平移立方体，平移量由 app.config 中的 SpongeTranslateIncrementFine 指定。
9. 要清除所有旋转，请单击“清除旋转”按钮。要清除所有平移，请单击“清除平移”按钮。

以下是在 app.config 中设置 SpongeRotateIncrement、SpongeTranslateIncrementCoarse 和 SpongeTranslateIncrementFine 的示例

<setting name="SpongeRotateIncrement" serializeAs="String">
	<value>15</value>
</setting>
<setting name="SpongeTranslateIncrementCoarse" serializeAs="String">
	<value>4</value>
</setting>
<setting name="SpongeTranslateIncrementFine" serializeAs="String">
	<value>0.5</value>
</setting>

稍加练习，您会发现可以轻松精确地移动立方体。在上面的图片中，我使用键盘通过以下步骤定向立方体

1. 使用 B 键打开背景，并使用减号键缩小
2. 按 X 键一次，使立方体沿其 X 轴旋转 15°
3. 按 Shift-Y 键两次，使立方体沿其 Y 轴旋转 -30°
4. 按 Z 键 3 次，使立方体沿其 Z 轴旋转 45°
5. 按 J 键两次，使其沿世界坐标 X 轴（南方）平移 8 个单位
6. 按 K 键两次，再按 Ctrl-K，使其沿世界坐标 Y 轴（向上）平移 8.5 个单位
7. 按 Ctrl-Shift-L，使其沿世界坐标 Z 轴（东方）负方向平移 0.5 个单位

旋转

3D 图形中的旋转和平移基于一个 4x4 矩阵，称为变换矩阵。左上角的 3x3 子矩阵表示旋转，矩阵底行的前三个元素表示平移。对于绕 X 轴旋转角度 theta，变换矩阵为

1      0          0         0
0 +cos(theta) +sin(theta)   0
0 -sin(theta) +cos(theta)   0
0      0          0         1

例如，如果您单击“清除旋转”按钮，然后按下 X 键，绕 X 轴旋转 15 度（其中 15 度的余弦值为 0.966，15 度的正弦值为 0.259），则矩阵的值将如 WPF 应用程序左侧所示，如下图所示

创建此变换矩阵的代码是

RotateTransform3D spongeRotateTransform3D = new RotateTransform3D();
spongeAxisAngleRotation3d.Axis = new Vector3D(1.0, 0.0, 0.0);
spongeAxisAngleRotation3d.Angle = 15.0;
spongeRotateTransform3D.Rotation = spongeAxisAngleRotation3d;

同样，绕 Y 轴旋转的变换矩阵为

+cos(theta)  0  -sin(theta)   0
     0       1       0        0
+sin(theta)  0  +cos(theta)   0
     0       0       0        1

例如，如果您单击“清除旋转”按钮，然后按下 Y 键，绕 Y 轴旋转 15 度，则矩阵的值将如 WPF 应用程序左侧所示，如下图所示

创建此变换矩阵的代码与上面绕 X 轴旋转的代码相同，只是旋转轴是 Y 轴

spongeAxisAngleRotation3d.Axis = new Vector3D(0.0, 1.0, 0.0);

最后，绕 Z 轴旋转的变换矩阵为

+cos(theta)  +sin(theta)   0  0
-sin(theta)  +cos(theta)   0  0
     0            0        1  0
     0            0        0  1

例如，如果您单击“清除旋转”按钮，然后按 Shift-Z 键两次，绕 Z 轴旋转 -30 度（注意负号）（其中 -30 度的余弦值为 0.866，-30 度的正弦值为 -0.5），则矩阵的值将如 WPF 应用程序左侧所示，如下图所示

创建此变换矩阵的代码与上面绕 X 轴旋转的代码相同，只是旋转轴是 Z 轴，角度是 -30

spongeAxisAngleRotation3d.Axis = new Vector3D(0.0, 0.0, 1.0);
spongeAxisAngleRotation3d.Angle = -30.0;

旋转实现

围绕立方体自身轴旋转的第一步是通过先前累积的旋转来变换世界坐标轴（作为单位向量），从而确定旋转轴。例如，假设经过任意次数的旋转后，按下了 X 键，这意味着我们想围绕立方体的 X 轴旋转它。首先，我们将世界坐标 X 轴（Point3D[] axes 数组的第一个元素）通过乘以累积旋转矩阵 saveCumulativeRotationMatrix，变换为其旋转后的对应物 Vector3D newX。

Point3D[] axes = new Point3D[] { new Point3D(1.0, 0.0, 0.0), 
                 new Point3D(0.0, 1.0, 0.0), new Point3D(0.0, 0.0, 1.0) };
saveCumulativeRotationMatrix.Transform(axes);
newX = new Vector3D(axes[0].X, axes[0].Y, axes[0].Z);

然后我们使用旋转后的 X 轴和旋转增量（以度为单位，如果按下了 Shift 键则为负）计算当前的变换矩阵 Matrix3D currentRotation，如上面的代码所示

spongeAxisAngleRotation3d.Axis = newX;
spongeAxisAngleRotation3d.Angle = currentShift ? -rotateIncrement : +rotateIncrement;
spongeRotateTransform3D.Rotation = spongeAxisAngleRotation3d;
Matrix3D currentRotation = spongeRotateTransform3D.Value;

为了保持旋转顺序，累积旋转存储在一个矩阵 Matrix3D saveCumulativeRotationMatrix 中，该矩阵乘以每个连续的旋转矩阵。由于每个连续的旋转都由 Matrix3D currentRotation 定义，因此乘法是

Matrix3D saveCumulativeRotationMatrix = Matrix3D.Multiply(saveCumulativeRotationMatrix, currentRotation)

要将旋转应用于模型，模型的 Transform 属性设置为 saveCumulativeRotationMatrix 矩阵

MatrixTransform3D matrixTransform3D = newMatrixTransform3D();
matrixTransform3D.Matrix = saveCumulativeRotationMatrix;
this.myGeometryModel.Transform = matrixTransform3D;

请注意，此相同的 Transform 被用于随立方体旋转的任何事物：裁剪平面、轴和面标签。

为了能够使用 Ctrl-Z 撤消旋转，累积旋转矩阵被添加到列表 private List<RotationHistory> previousRotationList 中。RotationHistory 类存储矩阵和 x、y、z 旋转。当按下 Ctrl-Z 时，添加到列表中的最后一个矩阵被移除，而前一个矩阵用作当前的累积旋转矩阵，从而“撤消”了上一次旋转。

翻译

在上一节中，我们围绕立方体自身的轴（因此也围绕其原点）旋转立方体，为清楚起见，没有考虑平移。在本节中，我们将考虑平移。当我们平移立方体时，我们是相对于世界坐标系平移它。（与相对于立方体坐标系发生的旋转不同。）如前所述，4x4 变换矩阵底行的前三个元素对应于平移。对于在 X、Y 和 Z 方向上分别平移 Xoffset、Yoffset 和 Zoffset 个单位，变换矩阵为

   1         0         0      0
   0         1         0      0
   0         0         1      0
Xoffset   Yoffset   Zoffset   1

例如，对于在 X 方向平移 4 个单位，Y 方向平移 8 个单位，Z 方向平移 -1.5 个单位（无旋转），变换矩阵的值将如 WPF 应用程序左侧所示，如下图所示

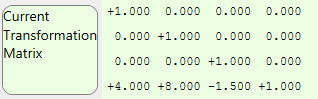
为了适应平移，使用了平移矩阵 Matrix3D spongeTranslationMatrix。使用上述值创建此矩阵的代码是

Transform3DGroup spongeTransformTranslateGroup = new Transform3DGroup();
TranslateTransform3D translateTransform3D = new TranslateTransform3D();
translateTransform3D.OffsetX = 4.0;
translateTransform3D.OffsetY = 8.0;
translateTransform3D.OffsetZ = -1.5;
spongeTransformTranslateGroup.Children.Add(translateTransform3D);
spongeTranslationMatrix = spongeTransformTranslateGroup.Value;

OffsetX、OffsetY 和 OffsetZ 的实际值由 TranslationKeys.HandleKeys() 根据是否按下 J、K 或 L 以及 Shift 和 Ctrl 键的状态计算。

Matrix3D spongeTranslationMatrix 包含沿世界坐标系的 X、Y 和 Z 平移。这些平移在旋转之前应用，因此平移立方体并围绕其自身轴旋转的完整代码是

Matrix3D currentRotation = this.spongeTransformRotateGroup.Value;
Matrix3D cumulativeRotation = Matrix3D.Multiply(saveCumulativeRotationMatrix, currentRotation);
Matrix3D translationAndRotation = Matrix3D.Multiply(currentRotation, spongeTranslationMatrix);
cumulativeRotationAndTranslation = 
       Matrix3D.Multiply(saveCumulativeRotationMatrix, translationAndRotation);
MatrixTransform3D matrixTransform3D = newMatrixTransform3D();
matrixTransform3D.Matrix = cumulativeRotationAndTranslation;
this.myGeometryModel.Transform = matrixTransform3D;

请注意，此相同的 Transform 被用于随立方体平移的任何事物：两个手电筒及其标签。

关注点

值得注意的是，无论 3D 模型有多少次平移和旋转，它都可以由一个 4x4 变换矩阵表示。

历史

• 版本 3.0.0.1