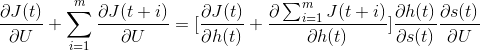ANNT：循环神经网络

• 下载源代码 - 608.1 KB

• 引言
• 理论背景
  • 循环神经网络 (RNN)
  • 长短期记忆 (LSTM)
  • 门控循环单元 (GRU)
  • 随时间反向传播
• ANNT 库
  • 构建代码
  • 使用示例
    • 时间序列预测
    • 序列预测（独热编码）
    • MNIST 手写数字分类
    • 生成城市名称
• 结论
• 链接
• 历史

引言

本文继续探讨人工神经网络及其在 ANNT 库中的实现。在前面两篇文章中，我们从基础知识开始，讨论了全连接神经网络，然后是卷积神经网络。提供了许多示例应用程序来处理回归和分类等不同任务。这次，我们将继续探索不同的人工神经网络架构，并着眼于循环神经网络——简单的 RNN，然后是 LSTM（长短期记忆）和 GRU（门控循环单元）。同样，我们将提供更多示例来演示循环神经网络的应用/训练。其中一些示例是新的——我们用全连接或卷积网络没有做过的。然而，有些示例将处理我们之前见过的问题（如 MNIST 手写数字分类），但方式不同，因此可以与其他架构进行结果比较。

重要提示：本文不是人工神经网络的入门介绍，而是循环神经网络的入门介绍。假定您已充分理解前馈神经网络及其使用梯度下降和反向传播算法进行训练的主题。如有需要，请随时回顾 ANNT 系列的前几篇文章。

理论背景

正如我们在之前的文章中所见，当输入表示为单个样本——特征向量、图像等时，前馈人工神经网络（全连接或卷积）在分类或回归任务中表现良好。然而，在现实生活中，我们很少处理脱离上下文的单个样本。给定一张图片，我们通常可以轻松地对其进行分类，并说出其中是否有花、水果、某种动物、物体等。但是，如果我们看到视频片段中某个人的一张图片，并被问及他将要执行什么样的动作/手势？我们可以大胆猜测，但在许多情况下，如果不观看视频片段并获得额外上下文，我们可能会猜错。文本/语音分析也是如此——仅凭一个词很难猜测主题。或者仅根据当前值预测某个时间序列的下一个值——如果不查看历史记录，很难说清楚。

这就是循环神经网络发挥作用的地方。与前馈网络一样，它们一次只接收一个样本。然而，循环网络可以建立它们之前看到内容的内部历史/状态。这使得有可能将样本序列呈现给这样的网络，它们的输出将不仅是对当前输入的响应，而且是对输入和当前状态组合的响应。

下面图片展示了循环单元的通用块图。其基本思想是向单元（神经元/层）引入额外的输入，这些输入连接到单元的输出。这导致循环单元的实际输入扩展为向量 X（提供的输入）和 H（历史）的组合。例如，假设一个循环单元有 3 个输入和 2 个输出。在这种情况下，时间 t 时的实际扩展输入成为一个包含 5 个值的向量：[x₁(t), x₂(t), x₃(t), h₁(t-1), h₂(t-1)]。将其转换为数值示例，假设该单元的初始输入向量 X 为 [1, 3, 7]。这会被扩展为向量 [1, 3, 7, 0, 0]，然后该单元对其进行内部计算（单元历史被初始化为零），可能会产生输出向量 Y 为 [7, 9]。下一个提供给该单元的样本是 [4, 5, 6]，例如，它会扩展为 [4, 5, 6, 7, 9]。依此类推。

然而，上面对循环单元的描述非常通用，并且提供了循环神经网络常见架构的简化视图。一些架构可能不仅具有从输出到输入的循环连接，而且还维护单元的额外内部状态。当然，不同的模型在内部执行的操作方面差异很大——通常，这远远超出了计算输入的加权和并应用激活函数。

到目前为止，循环单元被呈现为一个黑匣子。我们简要地接触了循环连接的想法，但没有说明单元内部进行了哪些计算。下面，我们将回顾一些流行的循环单元架构以及它们执行的计算类型以提供输出。注意：从现在开始，我们将循环单元视为人工神经网络中的层，如果需要，可以与其他层堆叠。

循环神经网络 (RNN)

标准的循环神经网络模型与全连接前馈神经网络非常相似。唯一的区别是，每个层的输出不仅成为下一层的输入，也成为该层本身的输入——输出到输入的循环连接。下面是标准 RNN 的块图，按时间展开，因此可以看到其输出 h(t) 是由提供的输入 x(t) 和历史 h(t-1)（时间 t-1 时的输出）计算得出的。

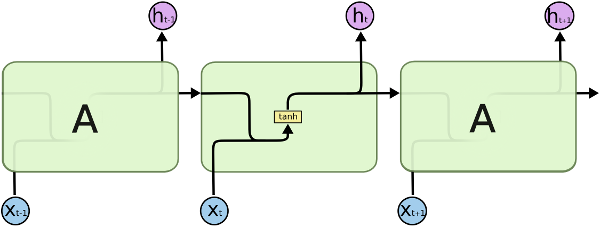
尽管上面的块图并未明确显示，但其中的 RNN 单元（块“A”）代表一个包含 n 个神经元的层，而不仅仅是一个神经元。这意味着其输出是一个包含 n 个元素的向量 h(t)。现在假设该层有 m 个实际输入（不包括循环输入），因此 x(t) 是一个包含 m 个元素的向量。总输入数则变为 m+n：m 个实际输入和 n 个历史值。然后，输出的计算方式与全连接层相同——其输入的加权和与偏置值相加，并通过激活函数（双曲正切）进行计算。在内部，RNN 层可能有一个大小为 (m+n)xn 的单个权重矩阵。然而，为了使方程更清晰，通常假设该层有两个权重矩阵：大小为 mxn 的矩阵 U，用于计算实际输入的加权和；大小为 nxn 的矩阵 W，用于计算历史向量的加权和。将这些组合在一起，得到 RNN 层输出的下一个方程：

引入循环连接允许 RNN 将先前的信息与当前提供的输入联系起来。这意味着，例如，在分析视频流时，它可以根据当前视频帧的内容对其进行分类，还可以考虑到先前呈现的视频帧。

然而，RNN 在过去能够记住多远？理论上，这些网络绝对可以处理长期依赖。实际上，这非常困难。正如我们后面将看到的，训练 RNN 的困难可能源于梯度消失。对于多层全连接前馈神经网络，我们遇到了将误差梯度从最后一层传播到前几层的问题，因为梯度在向后通过激活函数时可能会越来越小（消失）。在使用随时间反向传播算法训练循环神经网络时，需要将处理未来样本的误差梯度向后传播以处理过去样本。在这里，它需要一遍又一遍地通过激活函数向后循环。

结果是，简单的 RNN 可以将当前输入的输入与几步之前的输入联系起来。然而，随着过去和现在输入之间差距的增大，RNN 在学习这种联系方面会越来越挣扎。

长短期记忆 (LSTM)

为了解决简单 RNN 的问题，长短期记忆网络 (LSTM) 由 Hochreiter 和 Schmidhuber 于 1997 年提出，然后被许多其他研究人员推广和改进。LSTM 网络是一种特殊的 RNN，能够学习长期依赖。这些网络专门设计用于避免长期依赖问题。长时间记住信息是 LSTM 的默认行为，而不是它们难以学习的东西。

与简单 RNN 不同，单个 LSTM 块看起来复杂得多。它在内部执行更多的计算，并且除了其循环连接之外，还有一个内部状态。

LSTM 的关键在于单元的内部状态（在图的顶部水平穿过）。该单元能够向其内部状态添加或删除信息，这由称为门的结构控制。这些门控制必须保留或遗忘（删除）多少内部状态，必须向状态添加多少信息，以及状态对单元最终输出的影响程度。

LSTM 单元执行的第一步是决定在状态中保留哪些信息，哪些信息要丢弃。这个决定由一个称为遗忘门的 sigmoid 块做出。它接收输入 x(t) 和历史 h(t-1)，并生成一个在 (0, 1) 范围内的 n 个值的向量 f(t)（记住，n 是 LSTM 层输出的大小）。值为 1 表示按原样保留状态的相应值，值为 0 表示完全丢弃它，而值为 0.5 表示保留一半。

LSTM 计算的下一步是决定在单元状态中存储哪些信息。首先，一个双曲正切块创建一个包含新的候选状态值 Ĉ(t) 的向量，这些值将被添加到旧状态中。然后，另一个名为输入门的 sigmoid 块生成一个在 (0, 1) 范围内的值向量 i(t)，它表示有多少候选状态将被添加到旧状态中。与前面提到的向量 f(t) 类似，Ĉ(t) 和 i(t) 都是基于提供的输入 x(t) 和历史向量 h(t-1) 计算的。

现在该根据旧状态 C(t-1)、候选状态 Ĉ(t) 和向量 f(t) 和 i(t) 来计算新的 LSTM 单元状态了。首先，旧状态与向量 f(t) 相乘（逐元素），从而遗忘状态的一部分并保留另一部分。然后，候选状态与向量 i(t) 相乘，这决定了将多少候选状态纳入新状态。最后，将两部分相加，形成新的单元状态 C(t)。

最后一步是决定 LSTM 单元的输出向量是什么。单元的输出基于其当前状态通过双曲正切激活。然而，在上面进行了一些过滤，以决定输出哪些部分。这是通过使用另一个名为输出门的 sigmoid 块来完成的，该块生成一个向量 o(t)。将其与通过激活的双曲正切后的当前状态相乘，形成 LSTM 单元的最终输出 h(t)。

与简单 RNN 相比，以上所有内容肯定看起来更复杂。然而，您在尝试提供的示例应用程序时可能会发现，它确实提供了更好的结果。

门控循环单元 (GRU)

LSTM 网络有一些变体，多年来已被开发出来。其中一种变体是门控循环单元 (GRU)，它于 2014 年推出，并且自那时以来越来越受欢迎。它将遗忘门和输入门合并为一个更新门，即向量 z(t)。此外，它删除了单元的内部状态，仅使用提供的输入和历史向量进行操作。由此产生的模型比 LSTM 简单，并且通常表现出更好的性能。

随时间反向传播

在证明了 RNN、LSTM 和 GRU 网络的输出计算公式之后，现在是时候看看如何训练它们了。所有变体的循环神经网络都可以使用前几篇文章中描述的相同随机梯度和反向传播算法进行训练（第一篇和第二篇）。然而，在循环神经网络中，输出 h(t) 不仅取决于提供的输入 x(t)，还取决于先前的输出 h(t-1)，而 h(t-1) 又取决于输入 x(t-1) 和历史 h(t-2)。依此类推。由于我们存在循环网络输出之间的时间依赖性，因此我们需要在训练时考虑到这种依赖性。这导致算法的一个小变体，体现在其名称中——随时间反向传播 (BPTT)。

在训练前馈人工神经网络（全连接或卷积）时，训练样本是逐个呈现的（暂且忽略批量训练）——网络计算给定样本的输出，计算成本函数，然后将误差梯度向后传播通过网络更新其权重。然而，在训练循环神经网络时，我们处理的是序列，序列由一定数量的训练样本（输入/输出对）表示。这可能是一系列视频帧用于分类，一系列字母/单词/声音用于解释，一个表示某些时间序列值的序列——任何当前样本与过去样本之间的关系都很重要的情况。而且，由于序列的样本之间存在时间关系，我们不能使用单个样本来训练循环网络。相反，必须使用整个序列来更新网络的权重。

因此，这是训练循环网络的思路。我们首先将序列的第一个样本提供给网络，计算输出，计算成本值——将其与反向传播阶段稍后需要的一切一起存储。然后提供序列的第二个样本，计算输出，计算成本值——存储所有这些。依此类推——对序列中的所有样本都这样做。现在，我们应该有网络对序列中每个样本的输出以及基于计算出的输出和目标输出计算出的相应成本值。当序列中的所有样本一个接一个地提供给网络后，就可以开始反向传播并计算网络更新了。在这里，我们从序列的最后一个样本开始，并向时间反向移动。首先，根据成本 J(t) 对网络输出 h(t) 的偏导数计算权重更新。但更新不会立即应用，而是保留。然后我们移至时间 t-1 的前一个样本，并根据成本函数对该样本 J(t-1) 相对于输出 h(t-1) 的偏导数计算权重更新。然而，输出 h(t-1) 也用于计算未来输出 h(t)，这也会影响其成本值。这意味着在时间 t-1，我们不仅需要 J(t-1) 相对于 h(t-1) 的偏导数，还需要 J(t) 相对于 h(t-1) 的偏导数。对于时间 t-2 的样本，我们需要 3 个偏导数—— J(t-2)、 J(t-1) 和 J(t) 相对于 h(t-2)。依此类推。

你说这听起来有点令人困惑。但实际上，它并非如此。与多层前馈网络一样，所有更新规则都可以通过使用链式法则推导出来，该法则在第一篇文章中进行了描述。为了说明随时间反向传播算法的思想，让我们看看如何计算 RNN 网络中权重矩阵 U 的更新。为此，我们需要计算成本函数对该矩阵的偏导数。下面，我们可以看到如何为序列的最后一个样本做到这一点。与我们为全连接前馈网络获得的偏导数相比，我们可以看到它们是完全相同的。我们只改变了一些变量的命名，但除此之外没有其他更改。我们在这里得到的是 3 个偏导数的乘积：成本函数 J(t) 相对于网络输出 h(t)，网络输出相对于输入/历史/偏置的加权和 s(t)，以及加权和相对于矩阵 U。这就是链式法则以前所做的，并且现在仍然做得很好。

我们可以对序列中时间 t-1 的下一个训练样本——倒数第二个样本——做同样的事情。看起来更大，但链式法则的思想是相同的。

我们可以对时间 t-2 的另一个样本再做一次。一切都变得越来越大，越来越吓人，但希望它能展示某些计算中的递归模式。

再次为时间 t-2 的另一个样本重复一遍。一切都变得越来越大，越来越吓人，但希望它能展示计算中的递归模式。

稍微重构一下会更清楚……

尽管上面所有的链式法则看起来有点可怕，但在实现起来却相当容易。下面是简化版本，可用于计算成本函数对序列中任意样本的矩阵 U 的偏导数。关键在于，对于每个序列样本，成本函数对于未来样本的偏导数之和不会一遍又一遍地重新计算。与多层前馈人工神经网络中误差梯度从最后一层传播到前几层的方式相同，它通过时间从序列的最后一个样本传播到之前的样本。如果我们看看下面公式的右侧，我们会注意到方括号内的部分是两个偏导数的总和。第一个是当前样本的成本函数相对于当前输出的导数。第二个是未来样本的成本函数相对于当前输出的导数。总和的第二部分是在处理未来样本时预先计算的。因此，这里我们只需要将这两部分相加，然后乘以方括号后面的最后两个项。

出于几个原因，我们不在此提供确切的公式，而是保留它们作为导数链。首先，正如在上一篇文章中提到的，偏导数链的每个项都由其自身的构建块表示——例如全连接层、卷积层或循环层；sigmoid、双曲正切或 ReLU 激活函数；以及不同的成本函数。其中许多构建块之前已经讨论过，并且已经提供了它们的公式。因此，将它们组合在一起应该不是什么大问题。而且，由于所有这些构建块可以以多种方式组合，因此生成的公式可能看起来非常不同。根据所使用的成本函数，其相对于层输出的偏导数可能看起来大不相同。更重要的是，纯循环网络很少是这种情况。通常，一个神经网络可能包含一个或多个循环层，后面跟着一个全连接层。这意味着成本函数相对于循环层输出（而不是神经网络的最终输出）的偏导数会更长。但可以通过相同的链式法则推导出来。

无论如何，让我们尝试为 RNN 网络稍微完善一下。首先，我们将添加下标 k 来表示某个变量属于神经网络的第 k^th 层。其次，我们将使用 E_k(t) 来表示时间 t 的样本的成本函数相对于输出 h_k(t) 的偏导数——即时间 t 的第 k^th 层的输出。另外，让我们使用 E'_k(t) 来表示所有未来样本（从时间 t+1 到序列的最后一个样本）的成本函数相对于时间 t 的 RNN 第 k^th 层输出 h_k(t) 的偏导数之和。请注意，对于序列的最后一个样本， E'_k(t=last) 为 0。

这允许我们重写成本函数对网络参数的偏导数公式。使用这些公式，我们现在可以计算权重矩阵 U_k 和 W_k 以及偏置值 b_k 的梯度，然后将它们代入标准的 SGD 更新规则（或其他任何规则，如带有动量的 SGD 等）。

然而，我们仍然缺少一些部分。首先，我们需要将误差梯度传递到序列的前一个样本，即计算 E'_k(t-1)。而且，我们还需要将误差梯度传递到网络的前一层，即 E_k-1(t)。如果网络只有一个 RNN 层，那么 E_k-1(t) 的计算就会消失。

关于使用随时间反向传播算法训练循环网络的几点说明。如前所述，在计算网络参数的梯度时，它们不会立即应用——在处理完序列的每个训练样本后不会更新参数。相反，这些梯度会被累积。当整个序列的反向传播阶段完成时，这些累积的梯度将被代入 SGD 更新规则（或其他算法）。处理完序列并更新网络参数后会发生什么？网络的循环状态会被重置，然后处理新的训练序列。重置循环状态意味着将序列第一个样本的 h_k(t-1) 初始化为零（此时没有历史），并且对最后一个样本的 E'_k(t) 也做同样的处理（此时还没有来自未来成本的梯度）。

看来这就是 BPTT 训练 RNN 的全部内容了。如果有什么不清楚的地方，请记住这不是一篇可以独立学习的文章。相反，它继续了人工神经网络的主题，因此强烈建议您也回顾一下前两篇文章。

至于 LSTM 和 GRU 网络，我们在这里不推导它们的训练公式。由于它们比简单的 RNN 更复杂，因此训练它们本身就是一个主题。但是，如果您想研究这些神经网络，请记住训练它们（或任何其他 ANN 架构）所需的主要内容之一是对偏导数和链式法则的深刻理解。无论如何，这里有一些链接可以提供一些线索（LSTM，GRU 和另一个 GRU）。

ANNT 库

将 RNN、LSTM 和 GRU 层的实现添加到 ANNT 库中几乎是直接的——只需添加 3 个相应的类再加上一些小的调整，以便在处理循环网络时，训练代码能够识别序列。除此之外，该库保持了其原始结构，该结构在实现全连接和卷积人工神经网络时大部分已奠定。下面是更新的类图，与上一篇文章相比变化不大。

与库的其他部分一样，用于循环层的新类仅实现其前向和后向传递的数学运算，即仅计算导数链中自己的部分。这使得它们可以轻松地集成到现有框架中，并与其他类型的层混合。并且，遵循其他构建块的模式，新代码在可能的情况下利用了 SIMD 向量化和 OpenMP 并行。

构建代码

代码附带 MSVC（2015 版）解决方案文件和 GCC make 文件。使用 MSVC 解决方案非常简单——每个示例的解决方案文件都包含示例本身和库的项目。因此，MSVC 选项就像打开所需示例的解决方案文件并按构建按钮一样简单。如果使用 GCC，则需要先构建库，然后通过运行 make 来构建所需的示例应用程序。

使用示例

是时候将理论和数学放在一边了。取而代之的是，我们将着手构建一些神经网络并将其应用于一些任务。与上一篇文章中所做的一样，我们将有一些我们以前见过的应用程序，但采用不同的神经网络架构。此外，我们还将有一些我们以前没有尝试过的新应用程序。注意：这些示例均不声称所展示的神经网络架构是其任务的最佳选择。事实上，这些示例甚至没有说人工神经网络是最佳选择。相反，它们唯一的目的是演示如何使用该库。

注意：下面的代码片段只是示例应用程序的一小部分。要查看示例的完整代码，请参考文章提供的源代码包（其中还包括前几篇文章中描述的全连接和卷积神经网络的示例）。

时间序列预测

第一个演示示例是时间序列预测。这与我们在第一篇文章中用全连接网络解决的问题完全相同，但现在使用的是循环网络。该示例应用程序在指定数据的子集上训练神经网络，然后使用训练好的网络预测未包含在训练中的一些数据点。

与全连接网络（根据用于预测下一个值的前几个值数量而有多个输入）不同，循环神经网络只有一个输入。但这并不意味着单个值足以做出高质量的预测。循环网络还需要相当数量的历史数据。然而，这些数据是按顺序一个接一个地输入到网络中的，网络维护其自己的历史状态。

如上所述，训练循环网络有点不同。由于我们逐个输入值，网络会维护自己的状态，因此需要将训练数据集分成序列，然后使用随时间反向传播算法通过这些序列来训练网络。

假设提供了一个包含 10 个值的数据集

v0	v1	v2	v3	v4	v5	v6	v7	v8	v9
0	1	4	9	16	25	16	9	4	1

假设我们想预测 2 个值，然后比较预测精度。这意味着我们需要从提供的数据集中排除最后 2 个值（不将其用于训练）。最后，假设我们想生成长度为 4 步的序列。这将创建接下来的 4 个训练序列

0 ->  1 ->  4 ->  9 -> 16
1 ->  4 ->  9 -> 16 -> 25
4 ->  9 -> 16 -> 25 -> 16
9 -> 16 -> 25 -> 16 ->  9 

上面这 4 个序列中的每个序列都会生成 4 个训练样本。对于第一个序列，这些样本是（x – 输入，t – 目标输出）：

x	t
0	1
1	4
4	9
9	16

由于我们获得的 4 个序列是重叠的，因此我们将得到一些重复的输入/输出训练对。然而，这些将以不同的历史提供给神经网络。

默认情况下，示例应用程序创建一个 2 层神经网络——第一层是具有 30 个神经元的门控循环单元 (GRU)，输出层是具有单个神经元的完全连接层。然而，循环层的数量及其大小可以通过命令行选项进行覆盖。

// prepare recurrent ANN to train
shared_ptr<XNeuralNetwork> net         = make_shared<XNeuralNetwork>( );
size_t                     inputsCount = 1;

for ( size_t neuronsCount : trainingParams.HiddenLayers )
{
    net->AddLayer( make_shared<XGRULayer>( inputsCount, neuronsCount ) );
    net->AddLayer( make_shared<XTanhActivation>( ) );

    inputsCount = neuronsCount;
}
// add fully connected output layer
net->AddLayer( make_shared<XFullyConnectedLayer>( inputsCount, 1 ) );

假设训练数据样本按正确顺序呈现（一个序列的所有训练样本，然后是另一个序列的所有样本，依此类推），并且训练上下文配置了正确的序列长度，则训练循环将变得非常简单。注意：为简单起见，此示例在开始每个 epoch 时不打乱数据。训练循环神经网络时，需要打乱序列，但不能打乱单个训练样本（这会毁掉一切）。

// create training context with Nesterov optimizer and MSE cost function
XNetworkTraining netTraining( net,
                              make_shared<XNesterovMomentumOptimizer>
                              ( trainingParams.LearningRate ),
                              make_shared<XMSECost>( ) );

netTraining.SetTrainingSequenceLength( trainingParams.SequenceSize );

for ( size_t epoch = 1; epoch <= trainingParams.EpochsCount; epoch++ )
{
    auto cost = netTraining.TrainBatch( inputs, outputs );

    netTraining.ResetState( );
}

示例应用程序的输出不是特别有用，除了检查成本值是否下降以及检查最终预测误差。此外，该示例会生成一个输出 CSV 文件，其中包含 3 列：原始数据、训练结果（在提供原始数据作为输入时预测单个点）和最终预测（使用预测的点来预测新点）。

以下是一些结果示例。蓝线是我们提供给它的原始数据。橙色线是训练好的网络在取自训练集的输入上的输出。最后，绿线代表网络的预测。给定未包含在训练集中的数据，并记录输出。然后使用刚刚生成的输出进行进一步预测，然后再次进行。

对于这个特定的示例，循环网络未能像全连接网络那样展示出更好的结果。但是，通过仅使用一个过去的数值和内部维护的历史来查看预测结果仍然很有趣。

序列预测（独热编码）

这个示例应用程序的灵感来自这里的 LSTM 记忆示例，但我们增加了需要记忆的序列的数量和长度。该示例的思路是记忆 10 个略有不同的序列，然后在仅提供序列的第一个数字时正确输出它们。以下是循环网络需要记忆的 10 个序列

1 0 1 2 3 4 5 6 7 8 1
2 0 1 2 3 4 5 6 7 8 2
3 0 1 2 3 4 5 6 7 8 3
4 0 1 2 3 4 5 6 7 8 4
5 0 1 2 3 4 5 6 7 8 5

6 0 1 2 4 4 4 6 7 8 6
7 0 1 2 4 4 4 6 7 8 7
8 0 1 2 4 4 4 6 7 8 8
9 0 1 2 4 4 4 6 7 8 9
0 0 1 2 4 4 4 6 7 8 0 

前 5 个序列几乎相同，只有第一个和最后一个数字不同。其他 5 个序列也是如此，只有中间的模式发生了变化，但在所有这些序列中仍然相同。训练好的网络任务是首先为任何提供的输入输出 '0'，然后当输入为 '0' 时输出 '1'，当输入为 '1' 时输出 '2'，然后当输入为 '2' 时输出 '3' 或 '4'。等等。如果输入相同，它怎么知道选择 '3' 还是 '4'？是的，全连接网络无法处理这个问题。然而，循环网络具有内部状态（可以说是记忆）。这个状态应该告诉网络不仅要查看当前提供的输入，还要查看之前的内容。由于每个序列的第一个数字都不同，这使它们独一无二。因此，网络需要做的就是查看几步（有时是几步以上）。

为了解决这个预测任务，使用了一个简单的 2 层网络——第一层是循环层，第二层是全连接层。由于我们的序列中有 10 个可能的数字，并且它们是独热编码的，所以网络有 10 个输入和 10 个输出。

// prepare a recurrent ANN
shared_ptr<XNeuralNetwork> net = make_shared<XNeuralNetwork>( );

// basic recurrent network
switch ( trainingParams.RecurrrentType )
{
case RecurrentLayerType::Basic:
default:
    net->AddLayer( make_shared<XRecurrentLayer>( 10, 20 ) );
    break;

case RecurrentLayerType::LSTM:
    net->AddLayer( make_shared<XLSTMLayer>( 10, 20 ) );
    break;

case RecurrentLayerType::GRU:
    net->AddLayer( make_shared<XGRULayer>( 10, 20 ) );
    break;
}

// complete the network with fully connected layer and soft max activation
net->AddLayer( make_shared<XFullyConnectedLayer>( 20, 10 ) );
net->AddLayer( make_shared<XSoftMaxActivation>( ) ); 

由于每个序列有 10 个数字之间的转换，因此每个序列将生成 10 个输入/输出的独热编码训练样本。总共——100 个训练样本。这些都可以一次性输入到网络中。但是，为了使所有工作正常进行，必须告知网络序列的长度，以便随时间反向传播能够正确处理所有内容。

// create training context with Adam optimizer and Cross Entropy cost function
XNetworkTraining netTraining( net,
                              make_shared<XAdamOptimizer>( trainingParams.LearningRate ),
                              make_shared<XCrossEntropyCost>( ) );

netTraining.SetAverageWeightGradients( false );
// since we are dealing with recurrent network, 
// we need to tell trainer the length of time series
netTraining.SetTrainingSequenceLength( STEPS_PER_SEQUENCE );

// run training epochs providing all data as single batch
for ( size_t i = 1; i <= trainingParams.EpochsCount; i++ )
{
    auto cost = netTraining.TrainBatch( inputs, outputs );
    printf( "%0.4f ", static_cast<float>( cost ) );

    // reset state before the next batch/epoch
    netTraining.ResetState( );
} 

下面的示例输出显示，未经训练的网络会生成一些随机内容，而不是序列中的下一个数字。而训练好的网络能够重建所有序列。用全连接层替换循环层将会毁掉一切——无论是否训练过，网络都会失败。

Sequence prediction with Recurrent ANN

Learning rate  : 0.0100
Epochs count   : 150
Recurrent type : basic

Before training:
Target sequence:   10123456781
Produced sequence: 13032522355 Bad

Target sequence:   20123456782
Produced sequence: 20580425851 Bad

Target sequence:   30123456783
Produced sequence: 33036525351 Bad

Target sequence:   40123456784
Produced sequence: 49030522355 Bad

Target sequence:   50123456785
Produced sequence: 52030522855 Bad

Target sequence:   60124446786
Produced sequence: 69036525251 Bad

Target sequence:   70124446787
Produced sequence: 71436521251 Bad

Target sequence:   80124446788
Produced sequence: 85036525251 Bad

Target sequence:   90124446789
Produced sequence: 97036525251 Bad

Target sequence:   00124446780
Produced sequence: 00036525251 Bad

2.3539 2.1571 1.9923 1.8467 1.7097 1.5770 1.4487 1.3262 1.2111 1.1050
...
0.0014 0.0014 0.0014 0.0014 0.0014 0.0014 0.0013 0.0013 0.0013 0.0013


After training:
Target sequence:   10123456781
Produced sequence: 10123456781 Good

Target sequence:   20123456782
Produced sequence: 20123456782 Good

Target sequence:   30123456783
Produced sequence: 30123456783 Good

Target sequence:   40123456784
Produced sequence: 40123456784 Good

Target sequence:   50123456785
Produced sequence: 50123456785 Good

Target sequence:   60124446786
Produced sequence: 60124446786 Good

Target sequence:   70124446787
Produced sequence: 70124446787 Good

Target sequence:   80124446788
Produced sequence: 80124446788 Good

Target sequence:   90124446789
Produced sequence: 90124446789 Good

Target sequence:   00124446780
Produced sequence: 00124446780 Good 

MNIST 手写数字分类

下一个更有趣的示例是尝试——使用 GRU 网络进行MNIST 手写数字分类。我们已经用全连接和卷积网络完成了这个任务，所以看看循环网络在相同任务上能表现出什么 really 很有趣。然而，你可能会想，MNIST 图像中的时间依赖性在哪里？这对于根据前一个值预测序列（时间序列）的下一个值很清楚。但在这里，我们需要分类，而不是预测。而且我们处理的是单个图像。但是，如果我们稍微改变任务，一切都会变得清晰。我们不会像前馈网络那样一次性查看整个图像。相反，我们将逐行扫描它，并在最后得到分类结果。因此，我们不会直接输入 28x28 的 MNIST 图像，而是将 28 行像素逐个输入到循环网络。仅凭一行像素的图像来正确分类数字显然是不可能的。但是如果我们试图记住我们之前看到的其他行，那么这变得相当可行。

我们将用于此示例的人工神经网络看起来相当简单——GRU 层有 56 个神经元，然后是一个具有 10 个神经元的全连接层。

// prepare a recurrent ANN
shared_ptr<XNeuralNetwork> net = make_shared<XNeuralNetwork>( );

net->AddLayer( make_shared<XGRULayer>( MNIST_IMAGE_WIDTH, 56 ) );
net->AddLayer( make_shared<XFullyConnectedLayer>( 56, 10 ) );
net->AddLayer( make_shared<XSoftMaxActivation>( ) ); 

由于我们逐行将图像输入到循环神经网络，因此需要将每个图像分割成 28 个向量——每行像素一个。然后我们将它们按顺序提供给网络，并使用最后一个输出作为分类结果。这可能看起来像这样

XNetworkInference netInference( net );
vector<fvector_t> sequenceInputs;
fvector_t         output( 10 );

// prepare images rows as vector of vectors - sequenceInputs
// ...

// feed MNIST image to network row by row
for ( size_t j = 0; j < MNIST_IMAGE_HEIGHT; j++ )
{
    netInference.Compute( sequenceInputs[j], output );
}

// get the classification label of the image (0-9)
size_t label = XDataEncodingTools::MaxIndex( output );

// reset network inference so it is ready to classify another image
netInference.ResetState( ); 

现在是时候训练 GRU 网络并查看结果了

MNIST handwritten digits classification example with Recurrent ANN

Loaded 60000 training data samples
Loaded 10000 test data samples

Samples usage: training = 50000, validation = 10000, test = 10000

Learning rate: 0.0010, Epochs: 20, Batch Size: 48

Before training: accuracy = 9.70% (4848/50000), cost = 2.3851, 18.668s

Epoch   1 : [==================================================] 77.454s
Training accuracy = 90.81% (45407/50000), cost = 0.3224, 24.999s
Validation accuracy = 91.75% (9175/10000), cost = 0.2984, 3.929s
Epoch   2 : [==================================================] 90.788s
Training accuracy = 94.05% (47027/50000), cost = 0.2059, 20.189s
Validation accuracy = 94.30% (9430/10000), cost = 0.2017, 4.406s
...
Epoch  19 : [==================================================] 52.225s
Training accuracy = 98.87% (49433/50000), cost = 0.0369, 23.995s
Validation accuracy = 98.03% (9803/10000), cost = 0.0761, 4.030s
Epoch  20 : [==================================================] 84.035s
Training accuracy = 98.95% (49475/50000), cost = 0.0332, 39.265s
Validation accuracy = 98.04% (9804/10000), cost = 0.0745, 7.464s

Test accuracy = 97.79% (9779/10000), cost = 0.0824, 7.747s

Total time taken : 1864s (31.07min) 

从上面可以看到，我们在测试集上获得了 97.79% 的准确率。是的，未能击败卷积网络（其准确率为 99.01%）。但全连接网络（96.55%）只是输了。好吧，我们不打算说哪个网络更好或更差。测试的网络具有不同的架构、复杂性等，而且我们没有尝试找到这些网络的最佳配置。但仍然，能够看到循环网络通过一次查看一行像素并维护自己的过去记忆来对图像进行足够的分类，这很好。

生成城市名称

为了完成循环人工神经网络的演示，让我们尝试一些有趣的。最后一个示例尝试生成一些城市名称——随机的，但听起来或多或少自然。为此，使用美国城市数据集训练了一个循环人工神经网络。每个城市名称表示为字符序列，网络被训练以根据当前字符和先前字符的历史（网络的内部状态）来预测下一个字符。由于数据集中许多城市名称的字符序列存在矛盾（例如，“Bo”后面可以是“s”，如“Boston”，也可以是“u”，如“Boulder”，等等），因此网络不太可能记住任何名称。相反，它应该选择最常见的字符转换模式。网络训练完成后（经过一定数量的 epoch），它被用来生成新名称。网络接收一个或多个随机字符作为起始，然后其输出用于完成新生成的城市名称。

单词序列中的每个字符都经过独热编码——使用 30 个字符/标签：26 个用于 'A' 到 'Z'，3 个用于 '.'、'-' 和空格，1 个用于字符串终止符。结果是，神经网络有 30 个输入和 30 个输出。第一层是 GRU（门控循环单元），第二层是全连接层。

// prepare a recurrent ANN
shared_ptr<XNeuralNetwork> net = make_shared<XNeuralNetwork>( );

net->AddLayer( make_shared<XGRULayer>( LABELS_COUNT, 60 ) );
net->AddLayer( make_shared<XFullyConnectedLayer>( 60, LABELS_COUNT ) );
net->AddLayer( make_shared<XSoftMaxActivation>( ) ); 

辅助函数 ExtractSamplesAsSequence() 负责将词汇单词转换为训练序列。例如，如果需要编码的单词是“BOSTON”，那么它将生成下一个训练序列（尽管上面应用了独热编码）：

	0	1	2	3	4	5	...
输入	B	O	S	T	O	N	...
目标输出	O	S	T	O	N	null	...

由于此示例应用程序使用批量训练，因此每个训练序列必须具有相同的长度，即训练词汇中最长单词的长度。结果是，许多训练序列将被字符串终止符填充。

// create training context with Adam optimizer and Cross Entropy cost function
XNetworkTraining netTraining( net,
                              make_shared<XAdamOptimizer>( LEARNING_RATE ),
                              make_shared<XCrossEntropyCost>( ) );

netTraining.SetAverageWeightGradients( false );
/* sequence length as per the longest word */
netTraining.SetTrainingSequenceLength( maxWordLength );

vector<fvector_t> inputs;
vector<fvector_t> outputs;

for ( size_t epoch = 0; epoch < EPOCHS_COUNT; epoch++ )
{
    // shuffle training samples
    for ( size_t i = 0; i < samplesCount / 2; i++ )
    {
        int swapIndex1 = rand( ) % samplesCount;
        int swapIndex2 = rand( ) % samplesCount;

        std::swap( trainingWords[swapIndex1], trainingWords[swapIndex2] );
    }

    for ( size_t iteration = 0; iteration < iterationsPerEpoch; iteration++ )
    {
        // prepare batch inputs and outputs
        ExtractSamplesAsSequence( trainingWords, inputs, outputs, BATCH_SIZE,
                                  iteration * BATCH_SIZE, maxWordLength );

        auto batchCost = netTraining.TrainBatch( inputs, outputs );
        netTraining.ResetState( );
    }
}

为了演示训练好的网络可以生成一些有趣的内容，让我们先看看未经训练的网络生成的一些单词

• Uei-Dkpcwfiffssiafssvss
• Ajp
• Vss
• Oqot
• Mx-Ueom Lxuei-Kei-T
• Qotbbfss
• Ei-Mfkx-Ues
• Wfsssa

这是由训练好的神经网络生成的一些更有趣的城市名称的简短列表。是的，可能听起来有点不寻常。但仍然比“asdf”好。

• Bontoton
• Mantohantot
• Deranber
• Contoton
• Jontoron
• Gantobon
• Urereton
• Rantomon
• Mantomon
• Zontolen
• Zontobon
• Lentohantok
• Tontoton
• Lentomon
• Xintox
• Contovillen
• Wantobon
• Intoncon

结论

好的，以上是对一些常见的循环神经网络架构、它们的训练以及将其应用于不同任务的简要概述。ANNT 库已扩展了简单的循环神经网络 (RNN)、长短期记忆 (LSTM) 和门控循环单元 (GRU) 层的实现，以及演示库用法的其他示例应用程序。一如既往，所有最新代码都可以在GitHub上找到，并将获得新的更新、修复等。

在涵盖全连接、卷积和循环神经网络主题的三篇文章之后，似乎基础知识已经基本覆盖。该库的未来发展方向将是通过引入 GPU 支持来增加更多优化和性能提升，构建由图而非简单的层序列表示的更复杂的网络，涵盖新的有趣架构，如胶囊网络和生成对抗网络 (GAN) 等。我们将看看我们在列表上的进展。

链接

1. 循环神经网络
2. 深度学习基础——循环神经网络入门
3. 随时间反向传播和梯度消失
4. 理解 LSTM 网络
5. 理解 GRU 网络
6. LSTM 的反向传播：数值示例
7. 在门控循环神经网络中推导前馈和反向传播
8. GRU 单元
9. 长短期记忆网络的记忆演示
10. 独热编码
11. MNIST手写数字数据库

历史

• 2018年12月20日：初始版本