井字棋:轻松实现 AI
4.00/5 (8投票s)
一个简单无敌的井字棋实现。
引言
有些使用 AI 来与对手玩井字游戏的应用非常复杂。本文介绍了一种基于策略的简单方法,不使用递归算法或复杂的棋谱数据库。在此需要说明的是,“使用 AI”指的是示例应用能够模仿人类玩家的动作和反应,而不是那些只允许两个人对战的应用。这不是一个机器学习的练习,而更像是一个如何使用责任链模式来实现对人类对手走棋的结构化响应的例子。
基本策略
这里的思路是将构成棋盘的九宫格矩阵划分成八条线。每条线有三个格子。如果任何一方玩家占据了某一条线上的所有三个格子,他们就赢得了比赛。因此,这些线包括构成棋盘矩阵的 3 行、3 列和两条对角线。AI 在走棋之前会评估这些线的状态。
评估一条线
评估需要系统地进行。首先要检查的是潜在的制胜线。也就是 AI 已经占据了该线上 3 个格子中的 2 个,而第三个格子是空的。如果找不到制胜线,下一步是看对手是否能在下一步获胜。针对这种情况的走棋是强制性的,因为如果不这么走,游戏就会输掉。还有另一种不那么明显的强制性走棋,那就是对手有机会在下一步棋中同时形成两条制胜线。存在两条制胜线的情况被称为“叉子”(fork)。
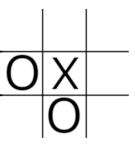
防止“叉子”
在上面的例子中,存在一个潜在的“叉子”,涉及到第 0 列的线和第 2 行的线。一个潜在的“叉子”包含两条共享一个公共格子的线,本例中是格子数组索引为 6 的位置。这两条线都被同一玩家占据,但每条线上只有一个格子被占据,并且这个格子不是共享的那个格子。当检测到这种情况时,就存在一个潜在的“叉子”。防御方法是堵住这两条线中的一条。
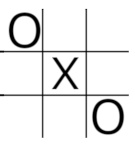
上图是一个双“叉子”,涉及第 0 列第 2 行和第 2 列第 0 行。防御方法与单个“叉子”相同——堵住其中一条线。但在这里,玩家X 绝不能占据角上的格子。因此,一个防止“叉子”的走棋应该先考虑占据该线三格数组中的中心格子,然后再选择其他格子。当 AI 检查了制胜线和潜在的“叉子”并且都没有发现时,它就可以走一步战略性的棋了。
战略性走棋
棋盘上所有格子的价值并非相等。中心格子是最强大的,因为它被四条线共享。其次是四个角上的格子,这些格子被三条线共享。可以说中心格子的影响力值为 4,角上格子的影响力值为 3。但这是假设所有共享这些格子的线都是活跃的。情况并非总是如此。一条已经被双方玩家占据的线实际上是无效的,所以该格子在这条线上的存在不应计入其影响力值。采用占据影响力值最高格子的策略,将总是导致 AI 在中心格可用时占据它,或者在中心格不可用时占据一个角上的格子。这对于避免下面所示的失败情景至关重要。
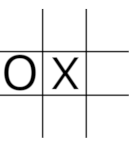
在玩家X占据中心后,玩家O未能占据一个角上的格子,导致输掉了比赛。
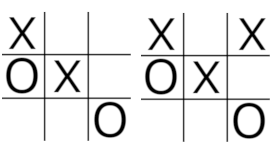
在代码中实现策略
这里的技巧是使用责任链模式,以避免在返回 AI (玩家X) 走棋的方法中使用多个和嵌套的 if then else 语句。这样一来,该方法就变成了
public Move MoveX(IBoard board)
{
this.board = board;
moveHandler.ReSet(board);
Move result = moveHandler.
HandleXWin().
HandleOWinOnNext().
HandlePossibleFork().
HandleStrategicMove().Result;
return result;
}
责任链中的每个 MoveHandler 方法都返回 MoveHandler 类的实例。这种安排使得可以以上述格式连续调用方法。所有方法都遵循类似的模式,正如在 HandleXWin 方法中可以看到的。
public MoveHandler HandleXWin()
{
if (IsHandled) return this;
if (gameScorer.BestScoreX == Constants.WinOnNextMove)
{
//this is a winning Line it has 2 X and 0 O
lineService.TryFindEmptySquare(gameScorer.BestLineX, out int index);
Result.Index = index;
Result.MoveResult= GameState.Xwin;
IsHandled = true;
}
return this;
}
它首先检查这步棋是否已经被处理,如果是,则返回 MoveHandler 实例。如果这步棋未被处理且它能处理,那么类型为 Move 的 Result 变量的 Index 属性会被设置为走棋的索引,其 MoveResult 属性被设置为结果 GameState,并且 IsHandled bool 值被设置为 true。该方法最后返回 MoveHandler 的实例。在责任链中最后一个方法被调用后,Result 变量的值将被返回。
public enum GameState
{
InPlay,
Xwin,
Owin,
Draw,
SearchCompleted//debugging
}
public struct Move
{
public int Index;
public GameState MoveResult;
}
使用辅助类
通过使用辅助类,责任链中的方法被简化为几行代码。
public MoveHandler HandleOWinOnNext()
{
if (IsHandled) return this;
if (gameScorer.BestScoreO == Constants.WinOnNextMove)
{
//O could win on its next move if the line is not blocked now
lineService.TryFindEmptySquare(gameScorer.BestLineO, out int index);
Result.Index = index;
IsHandled = true;
}
return this;
}
public MoveHandler HandleStrategicMove()
{
if (IsHandled) return this;
int index = gameScorer.GetBestImpactSquare();
Result.Index = index;
IsHandled = true;
return this;
}
public MoveHandler HandlePossibleFork()
{
if (IsHandled) return this;
if (lineService.TrySelectAntiForkSquare(board, out int index))
{
Result.Index = index;
IsHandled = true;
}
return this;
}
GameScorer 辅助类更新空格子的影响力值。
private void UpdateImpactScores()
{
ResetImpactScores();
foreach (var line in lines)
{
if (!line.IsLineBlocked )
{
UpdateImpactScoresForLine(line);
}
}
}
private void UpdateImpactScoresForLine(Line line)
{
for (int i = 0; i < 3; i++)
{
if (line.Squares[i].IsEmpty)
{
ImpactScores[line.Squares[i].BoardIndex] += 1;
}
}
}
LineService 类寻找潜在的“叉子”。
public bool TrySelectAntiForkSquare(IBoard board, out int result)
{
int[,] cornerLines = board.CornerLines;
for (int i = 0; i < cornerLines.GetLength(0); i++)
{
if (board.Lines[cornerLines[i, 0]].OScore == 1
&& board.Lines[cornerLines[i, 1]].OScore == 1
&& board[cornerLines[i, 2]].Content != 'O')
{
return TryFindEmptySquare(board.Lines[cornerLines[i, 0]],out result);
}
}
result = -1;
return false;
}
cornerLines 变量是一个三列的 int 数组,第一和第二列包含构成角的两条线的索引号,第三列是共享格子的索引号。
内容改变事件
当 Square 类的实例内容改变时,它会触发一个 SquareContentChangedEvent 事件。Line 类使用这个事件来更新自己的属性。
public class Line
{
public Square[] Squares = new Square[3];
public int Ocount { get; private set; }
public int Xcount { get; private set; }
public int XScore { get; set; }
public int OScore { get; set; }
public bool IsLineOblocked => Xcount > 0;
public bool IsLineXblocked => Ocount > 0;
public bool IsLineBlocked => IsLineOblocked && IsLineXblocked;
public Line(Square c0, Square c1, Square c2)
{
Squares[0] = c0;
Squares[1] = c1;
Squares[2] = c2;
foreach (var square in Squares)
{
square.SquareContentChangedEvent += SquareChangedEventHandler;
}
Update();
}
private void SquareChangedEventHandler(object sender, System.EventArgs e)
{
Update();
}
public void Update()
{
Xcount = 0;
Ocount = 0;
foreach (var square in Squares)
{
if (square.Content == 'X') Xcount++;
if (square.Content == 'O') Ocount++;
}
XScore = IsLineXblocked ? 0 : Xcount ;
OScore = IsLineOblocked ? 0 : Ocount ;
}
}
游戏引擎
游戏在 Game 类的 Play 方法中进行。
private Move Play()
{
inputOutputService.ShowBoard(board);
char firstPlayer = inputOutputService.GetIsYes(Constants.PromptGoFirst) ? 'O' : 'X';
char[] Players = firstPlayer == 'O' ? new char[] { 'O', 'X' } : new char[] { 'X', 'O' };
int moveNumber = 0;
Move move;
move.MoveResult = GameState.InPlay;
move.Index = -1;
while (move.MoveResult == GameState.InPlay)
{
char player = Players[moveNumber % 2];
move = player == 'X' ? MoveX(board) : MoveO();
board[move.Index].Content = player;
moveNumber++;
if (player == 'X')
{
inputOutputService.ShowBoard(board);
}
if (move.MoveResult == GameState.InPlay && moveHandler.IsGameADraw())
{
move.MoveResult = GameState.Draw;
}
}
inputOutputService.OutputGameResult(move, board);
return move;
}
只要每次走棋后返回的 Move struct 的 GameState 变量值为 InPlay,游戏就会继续。
无懈可击性测试
要使该应用被认为是无懈可击的,AI 必须能够处理其对手 玩家O 所有可能的走棋序列。第一步有 9 种走法,对于每一种第一步的走法,第三步(玩家O 的第二步)有 7 种走法,以此类推。一个递归算法应该能够实现这种情况。
private GameState PlayRecursiveMove(IBoard board, int depth, bool isPlayerO)
{
var unoccupiedSquares = board.GetUnOccupiedSquaresIndexes().ToList();
IBoard newBoard;
GameState result = GameState.InPlay;
if (isPlayerO)
{
for (int i = 0; i < unoccupiedSquares.Count; i++)
{
result = GameState.InPlay;
newBoard = board.Clone();
newBoard[unoccupiedSquares[i]].Content = 'O';
//debugging aid, stores move sequence
moves[depth] = unoccupiedSquares[i];
if (newBoard.Lines.Any((l) => l.OScore == Constants.WinningScore
&& result == GameState.InPlay))
{
inputOutputSerice.ShowBoard(newBoard);
OWinCount++;
totalMoves += unoccupiedSquares.Count + 1;
result = GameState.Owin;
}
if (newBoard.GetOccupiedSquaresCount() == Constants.TotalSquares
&& result == GameState.InPlay)
{
DrawCount++;
totalMoves += Constants.TotalSquares;
result = GameState.Draw;
}
if (result == GameState.InPlay)
{
result = PlayRecursiveMove(newBoard, depth + 1, false);
}
}
return GameState.SearchCompleted;
}
#region PlayerX
newBoard = board.Clone();
var move = MoveX(newBoard);
newBoard[move.Index].Content = 'X';
moves[depth] = move.Index;
if (newBoard.Lines.Any((l) => l.XScore == Constants.WinningScore))
{
XWinCount++;
totalMoves += unoccupiedSquares.Count + 1;
return GameState.Xwin;
}
if (newBoard.GetOccupiedSquaresCount() == Constants.TotalSquares)
{
totalMoves += Constants.TotalSquares;
DrawCount++;
return GameState.Draw;
}
return PlayRecursiveMove(newBoard, depth + 1, true);
#endregion
}
首先,该方法遍历所有可用的空格子列表。它为玩家O在当前迭代的格子上走一步,并检查结果。如果没有结果,该方法会再次被调用,但将IsplayerO bool值设置为false。这导致AI在递归的下一层进行走棋。如果没有结果,该方法再次被调用,这次将IsPlayerO设置为true,并在新的层级开始新的迭代。当在AI的走棋中找到结果时,该方法返回到上一层,并选择迭代中的下一个格子作为玩家O的走棋。同样,当在玩家O的回合中找到结果时,选择迭代中的下一个格子。这个过程一直持续到迭代完成,方法返回到上一层。AI对返回的结果除了将其传递给上一层外,不做任何处理。上一层是玩家O的回合,序列重复进行,直到所有走棋组合都被穷尽。以下是结果
| X 总获胜次数 | 364 |
| O 总获胜次数 | 0 |
| 总平局次数 | 125 |
| 总游戏次数 | 489 |
| 总步数 | 2673 |
结论
不使用递归或棋谱数据库,也可以玩出非常强大的井字游戏。
历史
- 2019年1月27日:初始版本
