65.9K
CodeProject 正在变化。 阅读更多。
Home

最小二乘法：Java 中的矩阵方法

Mark H Bishop
starIconstarIconstarIconstarIconstarIcon

5.00/5 (5投票s)

2019 年 1 月 31 日

GPL3

12分钟阅读

viewsIcon

18146

downloadIcon

714

计算类和 GUI 界面以说明用法。

sha256sum: 018750ea93e4b79791d97d1e746b64dedd0f7ded711b440c5ba2932ceb15dbaf

sha256sum: 863fa5f825fcd818c431590006517d8f572104b1c2f398490fb6531a32ac11b5

引言

许多学科都依赖线性回归来理解数据。大多数情况下，从业者会求助于已有的程序来完成计算。这些应用程序功能丰富且实用。然而，当您创建需要这些计算作为辅助的程序时，将您的程序与这些应用程序集成通常会显得笨拙或不便。有时，它们还有一个缺点，就是将底层算法隐藏在闭源代码中。

本文介绍了一组基本的 Java 类，用于执行矩阵计算，这些计算对于解决最小二乘法问题很有用，并包含一个用于演示用法的 GUI 示例。

背景

我开发 Java 类的主要参考资料是

Matrix Computations 3rd Edition，作者 Gene H. Golub 和 Charles F. Van Loan (Johns Hopkins University Press, Baltimore, 1996) (Golub)

从数学上讲，我们的目标是在已知矩阵 A 和向量 b 的情况下，求出一个向量 x，使得

Ax=b, where A is an m x n matrix, x is a vector of length n, and b is a vector of length m

当 m = n 时，称为确定性系统。当 m < n 时，我们有一个欠定系统，当 m > n 时，我们有一个超定系统。

线性回归

考虑一个联立方程组

如果我们把系数赋给矩阵 A，那么这个系统就可以表示为

确定性系统有唯一解。超定系统有无穷多个解。欠定系统要么没有解，要么有无穷多个解。我们希望我们的解是最小二乘解。在某些情况下（例如，超定、秩亏系统），存在无穷多个最小二乘解，并且我们可能希望进一步选择一个同时最小化特定范数的解，例如欧几里得范数。

线性回归在 A 的列大致独立或实现了处理相关列的机制时最为有用。我们如何评估列的依赖性？我们可以计算 A 的矩阵条件数，这是最高/最低奇异值的比率。条件数为 1 时是完美的。较大的数字表示列相关，如果我们要一个有用的回归方程，我们就需要一种方法来在合理的阈值内检测相关性。当出现不可接受的相关性时，我们就认为矩阵是秩亏的，并且，只要我们的方法能够处理秩亏，我们仍然可以获得有用的结果。

几种方法

高斯消元法（LU 分解）

class: MatrixLU.java

我们可以使用 LU 分解后进行回代来求解确定性系统。高斯消元法不处理秩亏。在存在不可接受的列相关性时，解对 A 的微小变化（扰动）非常敏感。它也受舍入误差的阻碍，这通常可以通过主元策略来缓解。它计算成本低廉，适用于条件适中的系统，并且已知不会受到浮点误差的影响。

正规方程组

class: NormalEquations.java

正规方程组方法适用于满秩系统*。它速度很快，但精度会因列相关性而受到不利影响。它不会显示，也不会处理秩亏。

*正如 NormalEquations.java 类中的实现那样，它不适用于欠定系统，因为其使用的 Cholesky 分解需要正定矩阵。可以通过显式构造 Inverse(A-transpose)(A)) 来修改该方法，但这会带来舍入误差的风险。

带列主元的 QR 分解

class: MatrixQR.java

带列主元的 QR 分解可以以一种检测秩亏（在指定阈值下）的方式实现（参见 Golub 算法 5.4.1 中的参数 τ）。当 rank < n 时，x 向量中不合要求的元素被设置为 0。参数 τ（tau）可以低至机器精度（在我 PC 上约为 10-15），但这对于在实际问题中有用地检测秩亏通常太低了。

完全正交分解

class: MatrixQR.java

对于秩亏系统，存在无穷多个最小二乘解。在某些应用中，从业者不在乎得到哪个解，只要函数拟合数据即可。在其他情况下，最好使用同时也是最小欧几里得范数解的最小二乘结果。完全正交分解提供了这样的解决方案。

奇异值分解

class: MatrixSvd.java

带主元的 QR 和完全正交方法都需要为秩确定阈值 τ 进行选择。τ 的合适选择是一个特定于应用程序的挑战。问题是：在什么点上列不相关性会影响结果的有用性？奇异值分解并不能回答这个问题，但检查它产生的奇异值向量可以提供细致的、揭示秩的信息（Golub 5.5.8）。最终，我们的问题只能通过了解正在研究的系统以及回归方程的用途来回答。

设置问题，一个例子

我最喜欢的例子来自：Crow, et. al., Statistics Manual with Examples Taken from Ordnance Development, Dover Publications Inc., NY, 1960。

（我坚信这个例子最初是在一个下午用铅笔和计算尺完成的。）

v1 v2 v3   y（产品直径）
11 58 11   126
32 20 13   92
14 22 28   108
26 55 28   119
9 41 21   103
30 18 20   83
12 56 20   113
29 40 26   109
7 38 9   130
28 57 10   106
10 19 19   104
31 37 18   92
12 21 10   94
33 40 11   95
9 42 27   109
12 57 29   103
10 21 12   82
33 40 19   85
30 58 29   104

我们的任务是提供一个公式，该公式根据工艺变量 v1、v2 和 v3 最佳地预测产品直径。

具体来说，我们要求提供常数系数 C、x1、x2 和 x3，它们通过以下形式的方程最佳地拟合数据

y = C + (x1)v1 + (x2)v2 + (x3)v3

在我们的矩阵表示 Ax=b 中，b 向量是产品直径的序列（m=19）。很容易认为 A 矩阵包含包含 v1、v2 和 v3 的三个列。这接近了，但在我们的目标方程中，我们需要一个常数，这就需要一个 n=4 的矩阵，其中第一列填充 1，其余列包含 v1、v2 和 v3（一个范德蒙德矩阵）。

结果是：

y = 95.74 - 0.5973v1 + 0.5151v2 - 0.0486v3

n 次回归解

有时，我们想要的回归方程是一个 n 次单变量多项式，而不是 n 维多变量多项式。例如，一个三次方程

y = a + (b)x + (c)x2 + (d)x3

考虑

在这种情况下，A 矩阵是一个范德蒙德矩阵，其中第 2、3 和 4 列分别是 x、x2 和 x3。这种情况下的解是非线性回归

y = 1.1  - 1.2x  + 1.3x2 -1.4x3

转换

假设您想查看数据与以下形式的方程拟合得有多好

y = exp(c0 + c1x + c2x2)

您可以使用范德蒙德方法来求解 Ax =ln(b)

ln(y) = c0 + c1x + c2x2

如何转换数据来拟合：y = αeβx ？

使用演示

您需要在您的机器上安装 Java。演示已在 Linux 和 Windows 上进行过测试。请确保您的 Java 是最新版本。根据您的操作系统，运行 Java.jar 文件通常就像双击一样简单。

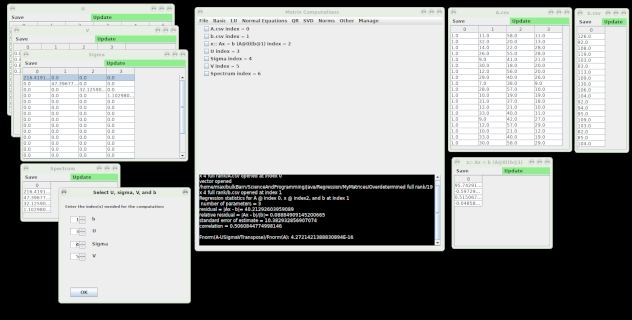
演示文件随附一些示例系统。您可以从文件菜单打开它们并进行实验。文件格式是标准的逗号分隔值结构。打开文件时，请注意它在主窗口中进行索引。在菜单中，使用索引指定您要用作操作参数的项目。请注意，在使用 LU、QR 和 SVD 菜单求解 Ax=b 之前，您必须先执行相应的分解。这是一个例子

  • 菜单 -> 文件 -> 打开 -> Matrix - 然后在 Examples/Overdetermined full rank/6 x 4 Rank 3 文件夹中查找并选择 A.csv 文件
  • 菜单 -> 文件 -> 打开 -> vector - 然后在同一文件夹中查找并选择 b.csv 文件。
  • 主窗口上的注释：A 的索引是 0，b 的索引是 1。
  • 菜单 -> SVD -> U,Sigma,V::A
  • 在弹出的窗口中选择矩阵索引 0，然后单击确定
  • 主窗口上的注释：b 在索引 1，U 在 2，Sigma 在 3，V 在 4
  • 菜单 -> SVD -> x::Ax = b - 按照上一步中的说明设置索引，确保将弹出窗口中的索引与主窗口上显示的正确索引匹配。（1, 2, 3, 4）
  • 菜单 -> Other -> Fit Statistics - 设置索引（0, 5, 1）并将 k 设置为 3（k 通常设置为矩阵秩，但在使用范德蒙德矩阵时设置为秩 -1（如您通过检查 A 的第一列所见）
  • 菜单 -> SVD -> Singular vector 显示 A 矩阵是秩亏的。
  • 您可以从 Manage 菜单关闭矩阵。清除除 A 和 b 之外的所有内容，然后尝试使用 tau 的默认值使用 QR 菜单。观察黑色控制台区域中的文本，您会看到它为 A 分配了秩 3。

复数应为格式：### [+/-]i###

  • 例如：5 +i2（注意空格）
  • 实部可能不存在，但首选 0 [+/-]i###
  • 您可以使用 j 代替 i
  • 您可以在末尾放置 i 或 j：### [+/-]###i

矩阵计算的绝妙之处在于，您可以随时检查结果。您可以使用 Excel 或 LibreOffice 合成自己的系统，将矩阵和向量另存为 csv 文件。务必测试您的结果。

Using the Code

项目 zip 是一个完整的 Eclipse Java 项目（版本：4.10.0）。源代码是 IDE 和平台无关的。有一个许可证文件：License.txt。项目中列出的类如下。每个类顶部附近都有一个 class responsibility 注释，总结了其用途。

计算类

有八个计算类

  • ComplexCalc.java
  • ComplexNumber.java
  • MatrixLU.java
  • MatrixOps.java
  • MatrixQR.java*
  • MatrixSvd.java
  • NormalEquations.java
  • Statistics.java

在您的实际应用中，只需要这些计算类，可能只需要其中的几个。例如，如果您有一个包含矩阵 A 的 double[ ][ ] 数组和一个包含向量 b 的 double[ ] 数组，那么可以构造一个一次性函数，例如使用 QR 主元方法计算 x

    public double[] GetX(double[][] A, double[] b) {        
        List<Object> oQR = MatrixQR.HouseholderCompactQRPivot(A, 0.00000000000001);
        double[][] QR = (double[][]) oQR.get(0);
        int rank = (int) oQR.get(1);
        int[] p = (int[]) oQR.get(2);
        double[] beta = (double[]) oQR.get(3);
        double[] x = MatrixQR.HouseholderCompactQRSolveX(QR, beta, p, rank, b);
        return x;
    }

矩阵是行主序数组。在下面的示例中，A 有 3 行 2 列（m = 3, n = 2）

double[][] A = new double[][] { { 0.1961, 0.3922 }, { 0.5883, 1.1767 }, { 0.7845, 1.5689 } };

*QR 方法（也用于 QR Ax=b 方法的输入）存在一些看似不寻常的返回参数，特别是 beta 向量。Beta 不是 QR 主元分解的必需元素，因为它可以根据需要从紧凑型 QR 中重新计算，但消耗此向量可以消除在多个后续函数中重新计算值的开销（参见 Golub 5.1.6）。

演示类

用于图形演示的类是

  • EventListener.java
  • FileOps.java
  • InputForm.java
  • MainForm.java
  • Master.java
  • MatrixForm.java
  • Operation.java
  • ParameterForm.java
  • StringUtils.java

MainForm.java 类是入口 GUI JFrame。它是一个顶层窗口，具有菜单，并显示活动的矩阵和向量以及每个矩阵和向量的唯一索引号。它还有一个文本区域（txtrConsole），用于发布来自 EventListener 接口的事件反馈（例如，文件打开操作的详细信息）或来自 MainForm 类中的 txtrConsole.append 命令的反馈（例如，统计结果）。

MatrixForm.java 类是一个 JFrame 容器，用于容纳单个矩阵和向量。Master.java 类保存应用程序运行的*所有*现有 MatrixForms 的集合（ArrayList<MatrixForm>），还包括实现从 MainForm 使用 MatrixForm 对象作为参数请求的各种计算的方法。这些对象被索引。当从 MainForm 菜单中选择一个操作时，会显示 ParameterForm，用户在此处指定与问题相关的矩阵/向量的索引。

演示中可用的操作在 Operations.java 中枚举。StringUtils.java 类用于将矩阵/向量转换为 csv 字符串。

关注点

我哥哥在 1964 年做一个高中科学项目，题为：“支持超铀元素存在性的数学证据。” 我看着他将一个正规方程组解法编程到一台打孔纸带计算机中，这是一个使用 jump 语句的了不起的实现。我从 20 世纪 70 年代开始使用 IBM 大型机的 Fortran IV 和打孔卡进行回归编程。后来，我转向了与实验室仪器接口的微型计算机，主要使用 HP-RPN 或 Pascal。在家，我使用了 Vic 20。在 21 世纪，我转向了 .NET 和 Java。

2003 年，我购买了 Golub/Van Loan 的《Matrix Computations》，并开始探索矩阵计算的丰富世界，特别关注求解线性系统。不用说，我是一个线性代数爱好者，而且，我得说，因为这个爱好，我在鸡尾酒会上非常有趣。

我有幸在 Gene Golub 于 2007 年去世前与他有过几次通信。矩阵数学丰富了我的生活，而《Matrix Computations》一书使这一切成为可能。

几篇参考文献

  • Bjorck, Ake, Numerical Methods for Least Squares Problems, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1996。
  • Golub, Gene H., Charles F. Van Loan, Matrix Computations 3rd Edition, The Johns Hopkins University Press, Baltimore, MD, 1996。
  • Pollock, D.S.G., A Handbook of Time-Series Analysis, Signal Processing and Dynamics, Queen Mary and Westfield College, The University of London, Academic Press, 1999。
  • Serber, George A. F., Alan J. Lee, Linear Regression Analysis, 2nd Edition, Wiley and Sons, Inc., Hoboken, NJ, 2003。
  • Watkins, David S., Fundamentals of Matrix Computations, 2nd Edition, John Wiley and Sons, Inc., New York, NY, 2002。

历史

  • 2019 年 1 月：文章提交
© . All rights reserved.