Soma Cube 求解器

• 下载源代码 - 224 KB

引言

该项目使用回溯算法来解决 Soma Cube 谜题，并允许您使用 WPF 渲染的 3D 图像来可视化算法的工作原理。

背景

我最近发现了 Kazem Jahanbakhsh 提出的一个有趣的 Soma Cube 求解算法。Soma Cube 是我 Soma Cube WPF 项目的主题。如果您不熟悉 Soma Cube 谜题，您可能需要阅读该文章以熟悉棋子的名称、棋子的立方体标签以及如何定向相机。

该算法首先放置 L 四面体，然后放置分支四面体，使其不与 L 四面体相交，然后放置右螺旋四面体，使其不与前两个棋子相交，依此类推，直到解开谜题。该算法使用一种称为回溯的技术。我所说的回溯是指，当算法在放置棋子时，如果一个棋子无法放置，则当前迭代停止，并使用不同的初始条件开始一个新的迭代。下面我将详细介绍算法的工作原理。

Using the Code

下载并解压解决方案，然后用 Visual Studio 打开 SomaCubeSolver.sln。它由以下项目组成

1. SomaCubeSolver - Kazem Jahanbakhsh 的 Java 代码，已转换为 C#。它生成的解决方案输出文件与 Java 版本相同（我使用 Eclipse Kepler Service Release 1 Build id: 20130919-0819 运行 Java 代码）。解决方案输出文件的名称是 solutions.txt。我在 Java 代码的基础上进行了一些小的改进：添加了注释；使用了 Dictionary 而不是 HashTable；使用了 const 而不是硬编码的数字；并使用了整数作为 Dictionary 键而不是字符串。
2. SomaCubeWPF2 - 一个 WPF 3D 应用程序，用于帮助可视化算法的运行。它使用 SomaCubeSolver 生成的文件，而 Java 版本不生成该文件。利用该文件，我将向您展示如何动画算法的运行。效果非常酷。SomaCubeWPF2 还有一个 UI，可以轻松可视化算法如何使用 BitArray 类。
3. SomaCubeLib - 由 SomaCubeWPF2 和 SomaCubeSolver 共享的库。

使用 Visual Studio 主菜单中的“生成”->“重新生成解决方案”来生成解决方案。由于前两个项目依赖于 SomaCubeLib 项目，因此该项目会先生成。Visual Studio 的一个不错的功能是通过右键单击解决方案，然后选择“项目生成顺序...”来设置此生成顺序。

立方体坐标和位数组

位数组

该算法的核心是 .NET BitArray 类。我使用这个类，因为它最接近 .NET 中 Java BitSet 类，而 Java BitSet 类用于原始 Java 代码。但是，Java BitSet 有一些 .NET BitArray 类缺失的方法，例如 AndNot 方法。我使用 C# 的出色扩展方法功能包含了缺失的方法。它们位于 SomaCubeLib 项目的 ExtensionMethods 类中。

立方体坐标

为了理解该算法，我们首先需要理解立方体坐标。想象一下将 27 个小立方体组装成一个单独的大 Soma Cube 并以原点为中心。小立方体编号为 0 - 26，其中立方体 0 位于 +1, -1, -1；立方体 1 位于立方体 0 上方 +1, 0, -1；立方体 2 位于立方体 2 上方 +1, +1, -1；立方体 3 位于立方体 1 旁边 0, -1, -1，依此类推，总共 27 个小立方体。您可能想花点时间熟悉一下如下图所示的编号系统（您还可能想打印 CubeNet.png，剪下图像并组装一个大型立方体的纸模型，显示编号的小立方体。）我们假设每个小立方体都是一个单位立方体，即其高度、宽度和深度均为一个单位。

算法

我将很快详细介绍算法，但作为高层次的介绍，我们首先假设我们从所有小立方体都为空的状态开始 Soma Cube。然后，我们将 L 四面体放置在小立方体位置 1、0、3 和 6，如下图所示。相应的 BitArray 对象将只有其 0、1、3 和 6 位被设置。换句话说，在表示大立方体的 BitArray 对象中，清除的位（0）表示小立方体未被占用，而设置的位（1）表示小立方体已被占用。图中未被占用（清除或 0）的小立方体显示为浅绿色，已被占用（设置或 1）的小立方体显示为灰色。（我很快会向您展示如何设置除灰色以外的颜色。）

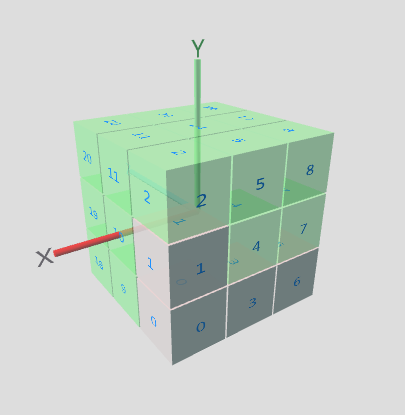
当算法运行时，策略是跟踪哪些小立方体被占用，哪些未被占用。如果小立方体未被棋子占用，算法将棋子放入空的小立方体中。例如，假设在算法运行一段时间后，除了立方体 22、25 和 26 之外，所有小立方体都被占用了，如下图所示（拥有您的纸模型对于想象这一点很有用。）算法随后可以确定 L 三面体可以放入此形状，因此将将其放置在未被占用的空间中，从而完成大 Soma Cube。

位运算 - 或、与、与非

在进入算法代码之前，我想谈谈我开发的一个工具，该工具用于帮助可视化 BitArray 对象上的位运算。如果您熟悉位运算，可以跳过本节。下图中，左侧，蓝色边框中的 27 位序列代表右侧的大 Soma Cube。紫色边框中的 27 位序列代表位（辅助位），这些位可以通过单选按钮或在标记为“十六进制数”的文本框中输入的十六进制数来设置。绿色边框中的 3 个按钮代表可以通过紫色边框中的位（辅助位）对蓝色边框中的位（立方体）执行的操作。按钮和操作是

1. 或 - 设置大 Soma Cube 中的位为 1 以添加棋子
2. 与 - 设置大 Soma Cube 中的位为 0 以测试是否可以添加棋子
3. 与非 - 清除大 Soma Cube 中对应位在指定 BitArray 中被设置的所有位；这用于移除棋子

“或”运算

要查看“Or”运算，例如，在大 Soma Cube 的 +Z 面上设置 S 四面体，请单击位 19、21、22 和 24 的单选按钮将其设置为 1。或在“十六进制数”文本框中输入 B4 并按“Enter”。位串“000 000 000 000 000 000 010 110 100”将显示在辅助位（紫色边框中的位）中。现在单击绿色边框区域中的“或”，并观察蓝色边框区域中的位与辅助位相同，并且大 Soma Cube 中相应的小立方体显示为灰色，表示它们已被占用，如下图所示。（此颜色可以在 app.Config 的 SmallCubeSetColor 中设置。）

要添加另一个棋子，例如 T 四面体，请单击位 0、9、10 和 18 的单选按钮将其设置为 1，或在“十六进制数”文本框中输入 40301B4 并按“Enter”。位串“100 000 000 110 000 000 110 110 100”将显示在辅助位中。接下来，单击菜单栏上的颜色并选择 T 四面体的颜色，然后单击绿色边框区域中的“或”，并观察蓝色边框区域中的位与辅助位相同，并且大 Soma Cube 中相应的小立方体显示为新的颜色，表示它们已被占用，如下图所示。随着算法的进展，它在代码中使用此“或”方法 - 像这样 theCube.Or(tempPiece) - 将棋子添加到大 Soma Cube 中，我们稍后将更详细地检查。

“与”运算

要查看“And”的工作原理，请按上面所述设置 S 和 T 四面体。单击紫色边框区域中的“清除”按钮。所有辅助位都已清除。假设我们想查看 L 三面体是否能放入大 Soma Cube 的位置 23、25 和 26。单击位 23、25 和 26，或在“十六进制数”文本框中输入 B 并按“Enter”。单击绿色边框区域中的“与”，并观察所有小立方体如何被清除，使大 Soma Cube 为空。算法使用此“And”方法来确定是否可以添加棋子。我们稍后会在一行代码 if (tempCube.IsEmpty()) 中看到这一点，以查看棋子是否能放入。

“与非”运算

要查看“AndNot”的工作原理，请按上面所述设置 S 和 T 四面体。单击紫色边框区域中的“清除”按钮。所有辅助位都已清除。将位 19、21、22 和 24 设置为 1，或在“十六进制数”文本框中输入 B4 并按“Enter”。这些位代表 S 四面体。单击绿色边框区域中的“与非”。请注意 S 四面体如何从大 Soma Cube 中移除。算法使用此“AndNot”方法来移除棋子。我们稍后会在一行代码 theCube.AndNot(tempPiece) 中看到这一点。

菜单栏“视图”

您可以使用菜单栏上的视图来关闭大 Soma Cube 的部分。例如，要查看非常中心的第 13 个小立方体，请单击“视图”->“+Z 层隐藏”。要恢复该层，请单击“+Z 层可见”。

非同构方向

既然我们已经涵盖了立方体坐标和位运算，接下来要理解的是零件的非同构方向。因为同构意味着“相同的形状”，例如，T 四面体在绕其 Y 轴旋转 180° 后具有“相同的形状”，如下图所示（请注意，面标签和轴不同，这表明它实际上被旋转了！）这是一个同构方向的例子。

相比之下，非同构旋转意味着零件在绕其 Y 轴旋转 180° 后具有“不同的形状”，如下图所示的 L 三面体。

每个零件的非同构方向存储在一个三维数组中。每个方向（在下面的代码片段中用 case 1、case 2 等表示）由 4 个 3D 点组成。对于 T 四面体，我用图示说明了轴和零件，使用立方体标签来显示方向。因此，例如，对于 case 1，零件沿 -Z 轴（因为所有 4 个点的 Z 均为 -1），T 四面体方向如下图所示。

大写字母 - D、B、A 和 C - 指的是第 1 部分中描述的零件的立方体标签。立方体标签显示在包含 4 个点的代码行上面的注释中。以下是 T 四面体非同构方向的代码片段

int[,,] TTetraCubeNonIsoOrient =
{
	//     D             B             A             C
	//  cube 4        cube 1        cube 2        cube 0
	{{ 0,  0, -1}, {+1,  0, -1}, {+1, +1, -1}, {+1, -1, -1}}, // case 1  Z=-1
	#region doc
	//          +Y
	//           |
	//         A |
	//         B D---  -X
	//         C
	// Freedom of movement will be {-1,  0, +2}
	#endregion

	//     A             B             C             D
	// cube 5          cube 4        cube 3       cube 1
	{{-1, -1, -1}, { 0, -1, -1}, {+1, -1, -1}, { 0,  0, -1}}, // case 2  Z=-1
	#region doc
	//          +Y
	//           |
	//           D---  +X
	//         A B C
	// Freedom of movement will be { 0, +1, +2}
	#endregion
...

Case 1 在下图的 Z=-1 平面上显示

在 Z=-1 平面上有 3 个其他方向，在 -X 平面上有 4 个，在 -Y 平面上有 4 个，总共 12 个方向。

除了这 12 个非同构方向中的每一个之外，还有一个三维整数数组，指示零件可以移动多少（您可以将其视为零件的“移动自由度”）。因此，对于 case 1，当 T 四面体在 Z=-1 平面和 X=+1 平面垂直方向时，移动自由度为 {-1, 0, +2}，这意味着零件可以沿 -X 方向移动 1 个单位，沿 Z 方向移动 2 个单位，并且不能沿 Y 方向移动（因为 T 四面体的高度为 3 个单位，与大 Soma Cube 相同。） 12 个移动自由度数组存储在二维数组 int[][] TTetraCubeFreedomOfMovement 中，在此示例中，二维数组是 12x3 的，因为有 12 个方向。

非同构方向的排列

给定七个 Soma 零件的方向和移动自由度，下一个挑战是确定特定方向的所有可能性。存储零件各种非同构方向的关键数据结构是一个 BitArray 对象列表：List<BitArray>。值得重复的是，每个 BitArray 对象有 27 位，每一位对应于上面显示的编号方案中的一个小立方体。清除的位（0）表示小立方体未被占用，而设置的位（1）表示小立方体已被占用。由于我们为七个 Soma 零件中的每一个都有一个列表，我们将使用一个由七个列表组成的数组来跟踪方向：pieceOrientationList = new List<BitArray>[NumPieces]。

FillPieceOrientationList() 方法获取非同构和移动自由度数组并构建方向列表。例如，对于 T 四面体，将 TTetraCubeNonIsoOrient 和 TTetraCubeFreedomOfMovement 数组传递给 FillPieceOrientationList()，后者又创建了 T 四面体的第六个方向列表 pieceOrientationList[5]。总共有 96 个 T 四面体的排列。下图显示了 Z=-1、Z=0 和 Z=+1 平面中的前 3 个排列

算法深入

现在我们已经涵盖了策略、BitArray 及其可对其执行的操作，并获得了零件方向的排列，是时候将它们整合在一起了。SomaCubeSolver 项目中的 BackTrack(int pieceNdx) 方法是实现这一切的关键。关键数据结构是 public BitArray theCube { get; set; }，因为它表示当前正在由七个零件构建的大 Soma Cube。BackTrack(int pieceNdx) 方法通过使用 pieceNdx 为 0 来调用启动。这会以 L 四面体开始大 Soma Cube，如这里所示，位于位置 0、1、3、6。算法运行时，L 四面体保持在此位置，并且零件按以下顺序放置

1. L 四面体（在整个运行过程中保持在 0、1、3、6 位置）
2. 分支四面体
3. 右螺旋四面体
4. 左螺旋四面体
5. S 四面体
6. T 四面体
7. L 三面体

然后递归调用 BackTrack(pieceNdx) 方法，其中 pieceIndex 为 1（第二个零件，分支四面体）。当 BackTrack(pieceNdx) 操作分支四面体时，使用 foreach 循环遍历其方向列表

	foreach (BitArray ba in pieceOrientationList[pieceNdx])
		

当 foreach 循环迭代时，theCube 的 DeepCopy 与当前方向“And”运算。如果当前方向不与 L 四面体相交，则 tempCube.IsEmpty() 将为 true（如上面所述），并且当前大 Soma Cube 与分支四面体的当前方向（在 12、15、16、24 位置）“Or”运算以添加分支四面体（粉红色）到大 Soma Cube（如上面所述）。这是上述代码的片段

	tempPiece = ba;
	tempCube = (BitArray) theCube.DeepCopy();
	tempCube.And(tempPiece);
	
	if (tempCube.IsEmpty())
	{
		theCube.Or(tempPiece);
	...

此时，这就是 theCube 的样子，其中包含灰色 L 四面体（在 0、1、3 和 6 位置）和粉色分支四面体（在 12、15、16 和 24 位置）。（我已将相机移动到 theta = 225，phi = -30，R = 12，以便从下方观察大 Soma Cube。）

然后我们递归调用 BackTrack(pieceNdx + 1) 来处理下一个零件，即右螺旋四面体。使用 foreach 循环遍历右螺旋四面体的方向列表，并确定其中一个方向（第七个）的 tempCube.IsEmpty() 为 true，因此右螺旋四面体将放入小立方体 4、7、8 和 17。当前立方体 theCube 与右螺旋四面体的当前方向进行 Or 运算。此时，这就是 theCube 的样子，其中 L 四面体（灰色）、分支四面体（粉色）和右螺旋四面体（黄色）放置在 4、7、8 和 17 位置，如下图所示

然后我们递归调用 BackTrack(pieceNdx + 1) 来处理下一个零件，即左螺旋四面体。在上面的 foreach 循环迭代 17 次后，左螺旋四面体（蓝色）放置在 11、13、14 和 22 位置，大 Soma Cube 开始成型，已有 4 个零件，如下图所示

算法再次递归调用 BackTrack(pieceNdx + 1) 来处理下一个（第五个）零件，即 S 四面体。它最初将 S 四面体放置在 9、10、19 和 20 位置，如下图所示

如果在遍历完整个 foreach 循环后，找不到可行的该零件方向，则 BackTrack() 的当前堆栈帧返回，并使用零件的另一个方向重新开始。当算法递归调用 BackTrack(pieceNdx + 1) 来处理下一个零件 T 四面体时，就会发生这种情况。换句话说，在上图的零件配置中，无法放置 T 四面体（如果您有 Soma 模型，您可能想像上图那样组装它来证明这一点。）S 四面体使用 theCube.AndNot(tempPiece) 移除，如上面所述，BackTrack() 返回，S 四面体被放置在另一个位置，并再次调用 BackTrack(pieceNdx + 1) 来处理下一个零件 T 四面体。最终，在左螺旋四面体处于该位置的情况下找不到解决方案，因此左螺旋四面体被移除，放置在另一个位置，并重复此过程，直到找到解决方案。它经过了近 6,000 次迭代，但找到了一个分支、右螺旋、左螺旋和 S 四面体（第二、第三、第四和第五个零件）的方向，使得 T 四面体（第六个零件）可以放置在 2、4、5、8 位置，如下所示

当 BackTrack() 方法成功放置了所有 7 个零件时，就找到了一个解决方案，这由以下表达式为 true 表示：if (pieceNdx == (NumPieces - 1))。这发生在 L 三面体（第七个也是最后一个零件）放置在 10、18 和 19 位置之后，经过 L 三面体超过 100 次 foreach 循环迭代。

解决方案动画

要查看算法的运行情况，SomaCubeWPF2 提供了一项功能，可以逐次迭代，就像使用调试器逐行调试代码一样。在菜单栏上，单击求解以显示解决方案步骤对话框。它读取 SomaCubeSolver 项目生成的由 SolutionFileName 变量（来自 SomaCubeLib）命名的文件，并在列表框中显示迭代。此文件代表 SomaCubeSolver 项目生成的 240 个解决方案中的一个。

当您单击“下一步”按钮时，将显示大 Soma Cube 的状态。最初，列表框中的第一行“0. L Tetra Cube”被选中。当您单击“下一步”时，将放置 L 四面体，位置为 0、1、3 和 6。下图显示，“下一步”按钮已单击三次，大 Soma Cube 现在由 L 四面体（深绿色，第一个放置的零件）、分支四面体（粉色）和右螺旋四面体（黄色）组成。

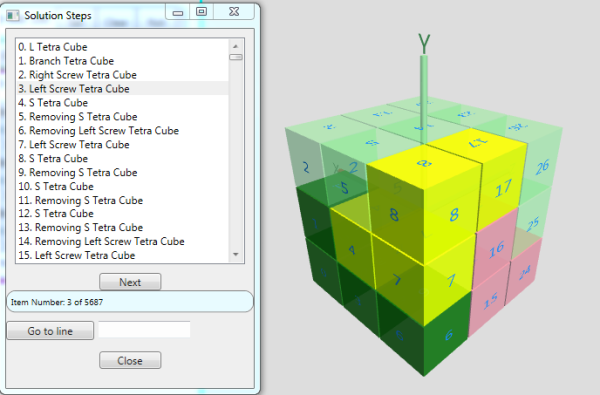
解决方案步骤对话框中选定的行现在显示“Left Screw Tetra Cube”。再次单击“下一步”按钮将放置该零件。由于此解决方案有近六千次迭代，因此逐步进行所有迭代既不切实际也不具启发性。相反，只需在“转到行”按钮旁边的文本框中键入 5675，然后单击“转到行”按钮。解决方案步骤对话框右下角的进度条将指示进度，因为它会遍历对话框中的每一行以获取大 Soma Cube 的当前状态。（更新进度条的代码使用了 BackgroundWorker 对象，并在我的 WPF Clipping Plane 项目中进行了描述。）第 5675 行 - 显示“5675. T Tetra Cube”的行 - 将被选中，如下图所示。单击“下一步”按钮一次将放置 T 四面体。当您单击“下一步”按钮 10 次时，您可以看到零件被移除和添加，并达到上面所述的状态。单击“下一步”按钮十二次，最后一次，将放置 L 三面体，从而解决大 Soma Cube。您还可以单击所需的行，然后使用“上一步”和“下一步”按钮。MessageReceived() 消息处理程序是在您单击某一行或使用“上一步”、“下一步”或“转到行”按钮时处理来自解决方案步骤对话框的消息的方法。

结论

Kazem Jahanbakhsh 的算法非常巧妙，而且由于它使用了位运算，因此也非常快。WPF 在 3D 图形方面非常出色，我认为该项目充分利用了 WPF 来可视化算法。

历史

• 2019 年 3 月 23 日：1.0.0.0