Tic Tac Toe - 人工智能实现

• 下载演示项目 - 15 Kb
• 下载源代码 - 12 Kb

摘要

此程序由 Mohit Soam 创建。这是我第一个真正的人工智能项目。注释易于理解，将帮助您开发涉及低级人工智能的类似程序。在大多数情况下，电脑是无法战胜的，但在少数情况下是可以战胜的。如果您似乎无法战胜它，您可能需要分析代码。

我唯一想改进的是游戏实际开始的方式。当人类点击一个未被占用的方格时，游戏就开始了。

使用代码

关于如何使用文章或代码的简要说明。类名和方法如下： 

'  ######         #######              #######        ###
'     #   #   ###    #    ###     ###     #    ###   #   #
'     #      #       #   #   #   #        #   #   #  ####
'     #   #  #       #   #   ##  #        #   #   #  #
'     #   #   ###    #    ##  ##  ###     #    ###    ####

类方法

Class_Initialize
构造函数为变量分配初始值。

Dim I As Integer
For I = 0 To 8
    HumanBox(I) = "Empty"
    MachineBox(I) = "Empty"
Next I

SetHuman
将玩家设置为人类。

SetMachine
将玩家设置为机器。

whoplay
返回玩家的姓名，即人类或机器。

If Play = False Then
    NowPlaying = "Human"
    Play = True
Else
    NowPlaying = "Machine"
   Play = False
End If

IsLegalMove
如果移动合法，则返回 true，否则返回 false。

If HumanBox(Index) = "Empty" And MachineBox(Index) = "Empty" Then
    IsLegalMove = True
Else
    IsLegalMove = False
End If

COMPARE
检查所有可能的获胜情况，如果有人获胜则返回 true。

Dim I As Integer
If NowPlaying = "Human" Then
    For I = 0 To 8
        EmptyBox(I) = HumanBox(I)
    Next I
ElseIf NowPlaying = "Machine" Then
    For I = 0 To 8
        EmptyBox(I) = MachineBox(I)
    Next I
End If
If (EmptyBox(0) = "1" And EmptyBox(1) = "1" And EmptyBox(2) = "1") Or _
    (EmptyBox(3) = "1" And EmptyBox(4) = "1" And EmptyBox(5) = "1") Or _
    (EmptyBox(6) = "1" And EmptyBox(7) = "1" And EmptyBox(8) = "1") Then
    COMPARE = True
ElseIf (EmptyBox(0) = "1" And EmptyBox(3) = "1" And EmptyBox(6) = "1") Or _
    (EmptyBox(1) = "1" And EmptyBox(4) = "1" And EmptyBox(7) = "1") Or _
    (EmptyBox(2) = "1" And EmptyBox(5) = "1" And EmptyBox(8) = "1") Then
    COMPARE = True
ElseIf (EmptyBox(0) = "1" And EmptyBox(4) = "1" And EmptyBox(8) = "1") Or _
    (EmptyBox(2) = "1" And EmptyBox(4) = "1" And EmptyBox(6) = "1") Then
    COMPARE = True
End If

评估机器移动的函数

 在人类移动后，轮到计算机评估最佳移动。我们调用 MachineMoveEvaluation 函数来执行此操作。

变量声明

Dim Move As Integer
Dim FinalMove As Integer
Dim LegalMove As Integer

Dim TotalScore As Integer
Dim HighestScore As Integer
Dim AverageScore As Integer
Dim RecursiveScore As Integer

Dim WasWin As Boolean
Dim WasLost As Boolean

Dim HumanBox As String
Dim MachineBox As String
    
Dim X As Integer

变量初始化

Const WS = 100
Const DS = 50

LegalMove = 0
TotalScore = 0
HighestScore = 0

评估最佳移动的主逻辑

TreeDepth = TreeDepth + 1

For Move = 0 To 8
If Box(TreeDepth - 1).IsLegalMove(Move) = True Then
    If LegalMove = 0 Then
        FinalMove = Move
    End If
    
    LegalMove = LegalMove + 1
    'Create New Object
    Set Box(TreeDepth) = New ClsTicTacToe
    For X = 0 To 8
        HumanBox = Box(TreeDepth - 1).GetHuman(X)
        MachineBox = Box(TreeDepth - 1).GetMachine(X)
        Call Box(TreeDepth).SetHuman(X, HumanBox)
        Call Box(TreeDepth).SetMachine(X, MachineBox)
    Next X

    Box(TreeDepth).NowPlaying = Box(TreeDepth - 1).NowPlaying
    Box(TreeDepth).Play = Box(TreeDepth - 1).Play
    Box(TreeDepth).FillBox (Move)
              
    If Box(TreeDepth).COMPARE = True Then
        WasWin = True
        HighestScore = WS
        TotalScore = TotalScore + WS
        FinalMove = Move
    Else
        Call Box(TreeDepth).whoplay
        S = MachineMoveEvaluation(RecursiveScore)

        If (RecursiveScore = WS) Then
            WasWin = True
        Else
            WasLost = True
            TotalScore = TotalScore + RecursiveScore
            If (RecursiveScore > HighestScore) Then
                HighestScore = RecursiveScore
                FinalMove = Move
            End If
        End If
        'Destroy Object
        Set Box(TreeDepth) = Nothing
    End If
End If
Next Move
 
If LegalMove = 0 Then
    S = DS
    TreeDepth = TreeDepth - 1
    MachineMoveEvaluation = 99
Else
    AverageScore = TotalScore / LegalMove
    If (WasWin = True And WasLost = True) Then
       S = WS - (WS - AverageScore) / 5
    Else
       S = AverageScore
    End If
    S = 100 - S
    TreeDepth = TreeDepth - 1
    MachineMoveEvaluation = FinalMove
End If

关注点

   此应用程序是生产系统的一个示例。生产系统应用于必须执行广泛搜索的问题解决程序。生产系统是符号人工智能系统。这两个术语之间的区别仅在于语义。符号人工智能系统可能不受生产系统严格定义的限制，但它们也不能有太大差异。

生产系统由三个部分组成：一个全局数据库，生产规则和一个控制结构。

全局数据库是系统的短期记忆。这些是待分析的事实集合。全局数据库的一部分代表系统环境的当前状态。例如，在国际象棋游戏中，当前状态可以代表所有棋子的位置。

生产规则（或简称生产）是条件性 if-then 分支。在生产系统中，每当系统中的一个或条件得到满足时，系统就可以执行或执行该规则下指定的特定操作。如果规则不满足，它可能会执行另一个操作。这可以简单地概括为

DATA (binded with initial global data base)
when DATA satisfies the halting condition do
    begin
    select some rule R that can be applied to DATA
    return DATA (binded with the result of when R was applied to DATA)
end

在生产系统试图为井字棋找到最佳移动的场景中，需要模式匹配来判断条件是否得到满足。如果井字棋的当前状态与期望状态（获胜状态或游戏解决方案）匹配，则游戏中有人获胜。但是，如果不是这种情况，系统必须尝试一个操作，该操作将有助于在生产规则下操纵全局数据库，从而使机器（即计算机）最终获胜。

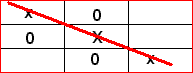初始状态	最终状态之一

为了仔细研究控制结构，让我们看一个涉及游戏的问题。井字棋包含九个空白方格，排列成一个三乘三的网格。玩家根据自己选择的标记，用“X”或“O”填充方格。在下一步，计算机出现在某个模糊的状态。生产系统的目标是达到某个最终状态（获胜状态）。这可以通过连续地将方格移入空位来获得。该系统随着方格的每一次移动而变化，因此，全局数据库随时间变化。系统的当前状态由方格的位置和枚举给出。例如，这可以表示为一个九维向量，其分量为 0、1、2、3、...、8、NULL，NULL 对象为空白空间。

在这个井字棋游戏中，最通用的生产规则可以简单地概括为一句话

首先填补使对手获胜的空方格，如果不这样做，则填补有助于我们赢得比赛的方格。

然而，为了填补空方格，系统必须首先验证对手获胜的所有可能移动（即，必须使用启发式搜索）。所有这些序列都需要进一步的生产规则。控制系统决定使用哪些生产规则以及按什么顺序使用。重申一下，为了找到获胜的情况。控制系统因此选择要在生产系统算法中使用的下一个生产规则（参见上面的生产系统算法图）。

致谢

本项目基于 Rohit Soam 在 MCA 学习期间在人工智能领域所做的工作。非常感谢！

历史

• v1.1 (2006年2月16日)
  首次发布