符号微分
4.89/5 (335投票s)
本文演示了如何使用堆栈对表达式进行微分,并显示输入表达式及其导数。
目录
引言
在本文中,我将描述如何解析数学表达式并识别其元素。我选择了一个简单的符号微分应用作为示例,以增加文章的价值并使读者受益最大。该应用程序(如上图所示)包含一个简单的网格,用于在同一视图中绘制输入曲线及其导数。我不会深入研究数学,因为这超出了本文的范围。我将在下一节中包含导数的定义。如果您对数学不感兴趣,可以跳过。
微分定义
函数f的导数可以解释为函数f在x处的值等于切线斜率,或者,f的导数可以解释为描述y相对于x在x点的瞬时变化率的函数。f关于x的导数也可以表示为
d(f(x))/dx,
or if y = f(x), dy/dx
微分公式
| 串口 | 表达式 | 导数 | 备注 |
u+v |
du/dx+dv/dx |
||
u-v |
du/dx-dv/dx |
||
u/v |
(v*du/dx-u*dv/dx)/v^2 |
||
u*v |
u*dv/dx+v*du/dx |
||
c*u |
c*du/dx |
c 为常数 |
|
u^v |
v*u^(v-1)*du/dx+u^v*ln(u)*dv/dx |
||
u^n |
n*u^(n-1)*du/dx |
n 为实数 |
|
c^u |
c^u*ln(c)*du/dx |
c 为常数 |
|
e^u |
e^u*du/dx |
e = 2.7182818284590452353602874713527 |
|
| 1 | sin(u) |
cos(u)*du/dx |
|
| 2 | cos(u) |
-sin(u)*du/dx |
|
| 3 | tan(u) |
sec(u)^2*du/dx |
|
| 4 | sec(u) |
sec(u)*tan(u)*du/dx |
|
| 5 | cosec(u) |
-cosec(u)*cot(u)*du/dx |
|
| 6 | cot(u) |
-cosec(u)^2*du/dx |
|
| 7 | sinh(u) |
cosh(u)*du/dx |
|
| 8 | cosh(u) |
sinh(u)*du/dx |
|
| 9 | tanh(u) |
sech(u)^2*du/dx |
|
| 10 | sech(u) |
sech(u)*tanh(u)*du/dx |
|
| 11 | cosech(u) |
cosech(u)*coth(u)*du/dx |
|
| 12 | coth(u) |
-cosech(u)^2*du/dx |
|
| 13 | asin(u) |
1/sqrt(1-u^2)*du/dx |
|
| 14 | acos(u) |
-1/sqrt(1-u^2)*du/dx |
|
| 15 | atan(u) |
1/(1+u^2)*du/dx |
|
| 16 | asec(u) |
1/(|u|*sqrt(u^2-1))*du/dx |
|
| 17 | acosec(u) |
-1/(|u|*sqrt(u^2-1))*du/dx |
|
| 18 | acot(u) |
-1/(1+u^2)*du/dx |
|
| 19 | asinh(u) |
1/sqrt(u^2+1)*du/dx |
|
| 20 | acosh(u) |
1/sqrt(u^2-1)*du/dx |
|
| 21 | atanh(u) |
1/(1-u^2)*du/dx |
|
| 22 | asech(u) |
-1/(u*sqrt(1-u^2))*du/dx |
|
| 23 | acosech(u) |
-1/(u*sqrt(1+u^2))*du/dx |
|
| 24 | acoth(u) |
1/(1-u^2)*du/dx |
|
| 25 | sqrt(u) |
1/(2*sqrt(u))*du/dx |
|
| 26 | log10(u) |
1/(u*ln(10))*du/dx |
|
| 27 | log(u) |
1/u*du/dx |
|
| 28 | ln(u) |
1/u*du/dx |
|
| 29 | sign(u) |
0 |
|
| 30 | abs(u) |
u/|u|*du/dx |
|u| 是 abs(u) |
数学表达式
数学表达式包括数字、运算符、函数、变量和操作符。运算符包括+、-、*、/和^。函数如sin(x),变量如x。我们的目标是识别每个元素,并将其正确的微分规则应用于该元素或一组元素。
Expression examples:
sin(2*x)/x
sin(45+cos(2)/tan(x)
sign(cos(x)
32*9-8/2
微分步骤
表达式解析填充堆栈
表达式解析是扫描表达式以查找其元素(数字、运算符、函数和变量)的过程。每个运算符都应该有两个操作数;例如,取 2*12。“*”运算符有两个操作数:2 和 12。每个函数都有其参数。例如,对于sin(x),函数是sin,参数是x。因此,我们应该以特定的方式扫描表达式,以识别每个运算符及其操作数,以及每个函数的参数,从而简化计算或微分。
表达式的执行取决于运算符优先级。如果我们能够构建一个运算符和操作数的堆栈,使得每个运算符后面都跟着它的两个操作数,那么 2*12 应该构建这个堆栈:“*”,“2”,“12”。因此,计算函数会检查堆栈。如果项目是运算符,则它会取它的两个操作数,并以递归公式对它们进行计算,这样整个表达式就可以被计算出来。例如,表达式
sin(2*12)/7+9^2
…应该按以下步骤计算
- 计算
sin(2*12)/7 - 计算
9^2 - 然后将两个结果相加
- 要计算第1点,我们需要
- 计算
sin(2*12) - 计算 7
- 然后将两个结果相除
- 要计算第 4.1 点,我们需要
- 计算
2*12 - 将
sin函数应用于结果 - 要计算第 4.4.1 点,我们需要
- 将运算符
*应用于两个操作数 2 和 12
- 将运算符
- 计算
- 计算
执行扫描的函数接受输入表达式和一组取决于其优先级的操作数,如下面的代码所示
///////////////////////////////////////////////////////////
// GetOperator: scan the input string
// to search for any of the input operators
///////////////////////////////////////////////////////////
int GetOperator(IN LPCSTR lpcs, IN LPCSTR lpcsOperators[])
{
for(int nIndex = 0; lpcsOperators[nIndex]; nIndex++)
{
int nOpen = 0;
// scan the expression from its end
LPSTR p = (LPSTR)lpcs+strlen(lpcs)-1;
// loop tells reach expression start
while(p >= lpcs)
{
// check for close
if(*p == ')')
nOpen++;
// check for open
else if(*p == '(')
nOpen--;
// check for operator
else if(nOpen == 0 && strchr(lpcsOperators[nIndex], *p) != NULL)
// check if the operator in not a sign mark
if((*p != '-' && *p != '+') ||
(p != lpcs && IsRightSign(*(p-1),
lpcsOperators, nIndex+1)))
// return operator index
return (int)(p-lpcs);
p--;
}
}
// operator not found
return -1;
}
现在很明显这是一个递归操作。要做到这一点,我们需要将表达式形式化为运算符和操作数的堆栈,并以特定的方式处理该堆栈以获得最终结果。简而言之,这样做主要步骤是
- 查找运算符
- 在运算符索引处分割表达式
- 将两个结果操作数添加到堆栈
- 如果未找到运算符,则检查表达式是否以函数名开头
如果应用上述步骤,我们将得到如下形式的堆栈
| + | ||||
| / | ||||
| sin(2*12) |
|
|||
| 7 | ||||
| ^ | ||||
| 9 | ||||
| 2 |
为了更详细地描述这一点,让我们看看解析表达式并填充堆栈的代码
bool FillStack(LPCSTR lpcsInput, vector<EXPRESSIONITEM*>& vStack)
{
// operators array from high to low
priority LPCSTR lpcsOperators[] = { "+-", "*/", "^%", NULL };
// insert first input into the stack
vStack.push_back(new ExpressionItem(lpcsInput));
// loop in Expression stack to check if
// any Expression can be divided to two queries
for(int nIndex = 0; nIndex < (int)vStack.size(); nIndex++)
// check if Expression item is operator
if(vStack[nIndex]->m_cOperator == 0)
{
// copy Expression string
CString str = vStack[nIndex]->m_strInput;
// parse expression to find operators
int nOpIndex = GetOperator(str, lpcsOperators);
if(nOpIndex != -1)
{
// split the Expression into
// two queries at the operator index
vStack[nIndex]->m_cOperator = str[nOpIndex];
// add the left operand of the
// operator as a new expression
vStack.insert(vStack.begin()+nIndex+1,
new ExpressionItem(str.Left(nOpIndex)));
// add the right operand
// of the operator as a new expression
vStack.insert(vStack.begin()+nIndex+2,
new ExpressionItem(str.Mid(nOpIndex+1)));
}
else
// check if Expression string
// starts with function or parenthesis
if((vStack[nIndex]->m_nFunction = GetFunction(str,
vStack[nIndex]->m_nSign)) == 0
&& vStack[nIndex]->m_nSign == 0)
// remove parentheses and re-scan the Expression
vStack[nIndex--]->m_strInput =
str.Mid(1, str.GetLength()-2);
}
return true;
}
现在没有人能否认这是你能找到的最简单的数学表达式解析代码。我们可以将其注释整理成以下几点:
- 将第一个输入插入堆栈
- 循环遍历表达式堆栈,检查是否可以将任何表达式分为两个查询
- 检查表达式项是否为运算符(+-*/^)
- 解析表达式以查找运算符
- 如果找到运算符
- 在运算符索引处将表达式分割成两个查询
- 将运算符的左操作数添加为新表达式
- 将运算符的右操作数添加为新表达式
- Else
- 检查表达式字符串是否以函数或括号开头
- 如果找到函数,则在表达式数据中设置其编号
对堆栈应用微分公式
应用微分公式意味着遍历堆栈,获取每个运算符,并根据运算符在运算符的两个操作数上应用微分规则
| 表达式 | 导数 |
u+v |
du/dx+dv/dx |
u-v |
du/dx-dv/dx |
u/v |
(v*du/dx-u*dv/dx)/v^2 |
u*v |
u*dv/dx+v*du/dx |
c*u |
c*du/dx |
u^n |
n*u^(n-1)*du/dx |
c^u |
c^u*ln(c)*du/dx |
e^u |
e^u*du/dx |
如果任何操作数是运算符,则再次以递归方式调用函数来微分整个表达式。下面的代码代表了这个函数
CString DifferentiateStack(vector<EXPRESSIONITEM*>& vStack, int& nExpression)
{
ExpressionItem *pQI = vStack[nExpression++];
if(pQI->m_cOperator)
{
// get left operand
CString u = vStack[nExpression]->GetInput();
// get left operand differentiation
CString du = DifferentiateStack(vStack, nExpression);
// get right operand
CString v = vStack[nExpression]->GetInput();
// get right operand differentiation
CString dv = DifferentiateStack(vStack, nExpression);
if(du == '0') // u is constant
...
else if(dv == '0') // v is constant
...
else
switch(pQI->m_cOperator)
{
case '-': // d(u-v) = du-dv
case '+': // d(u+v) = du+dv
pQI->m_strOutput = '('+du+pQI->m_cOperator+dv+')';
break;
case '*': // d(u*v) = u*dv+du*v
pQI->m_strOutput = '('+u+'*'+dv+'+'+du+'*'+v+')';
break;
case '/': // d(u/v) = (du*v-u*dv)/v^2
pQI->m_strOutput = '('+du+'*'+v+'-'+u+'*'+dv+")/("+v+")^2";
break;
case '^': // d(u^v) = v*u^(v-1)*du+u^v*ln(u)*dv
pQI->m_strOutput = '('+v+'*'+u+"^("+v+"-1)*"+ du+
'+'+u+'^'+v+"*ln("+u+")*"+dv+')';
break;
}
}
else
// get Expression differentiation
pQI->GetDifferentiation();
// return resultant differentiation
return pQI->m_strOutput;
}
优化方程
优化方程包括以下简单步骤:
- 将“--”替换为“”或“+”
- 将“+-”替换为“-”
- 将“((....))”替换为“(....)”
- 删除任何“1*”
- 删除任何“*1”
- 删除任何“^1”
- 删除任何“1*”
- 删除不必要的括号
微分伪代码
Differentiate(input)
{
Stack = FillStack(input)
output = DifferentiateStack(Stack)
Optimize(output)
return output
}
FillStack(input)
{
operators[] { "+-", "*/", "^%" }
stack.push(input)
loop( n = 1 to stack.size() )
{
if stack[n] is not operator
if GetOperator(stack[n],
operators) success
{
Split stack[n]
stack.Insrt(left operand)
stack.Insrt(right operand)
}
else
GetFunction(stack[n])
}
}
DifferentiateStack(stack, index)
{
if stack[index] is operator
{
index++
u = stack[index]
du = DifferentiateStack(stack, index)
v = stack[index]
dv = DifferentiateStack(stack, index)
if operator = '-' or '+'
output = du+operator+dv
else if operator = '*'
output = u*dv+du*v
else if operator = '/'
output = (du*v-u*dv)/v^2
else if operator = '^'
output = v*u^(v-1)*du+u^v*ln(u)*dv
}
else
output = stack[index++].GetDifferentiation()
return output
}
void Optimize(str)
{
replace "--" with "" or "+"
replace "+-" with "-"
replace "((....))" with "(....)"
remove any 1*
remove any *1
remove any exponent equal 1
remove unneeded parentheses
if str changed then
Optimize(str)
}
ExpressionItem::GetDifferentiation()
{
if Function then
{
arument = Argument(input);
if function = SIN
output = Differentiate(arument)*cos(arument)
else if function = COS
output = Differentiate(arument)*(-sin(arument))
else
...
}
}
else
{
if input = "x"
output = "1"
else if input = "-x"
output = "-1"
else if input is numeric
output = "0"
else
output = "d"+input+"/dx"
}
}
程序选项卡
微分
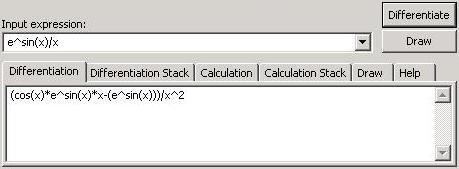
微分选项卡在输入表达式上应用微分步骤后显示微分结果。输入表达式在微分前进行计算,以优化包含数字的任何算术部分,如示例所示
e^sin(pi/3)/tan(x) 被优化为 2.377442/tan(x),然后进行微分得到结果 (-2.377442*sec(x)^2)/(tan(x))^2。
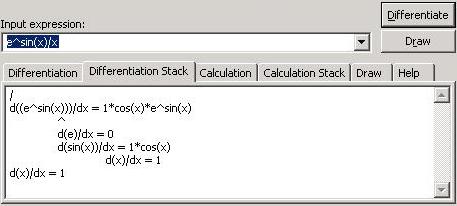
微分堆栈
计算
此选项卡是一个符号计算器,可以计算任何复杂的数学表达式。计算仅包含两个常量
e = 2.7182818284590452353602874713527
pi = 3.1415926535897932384626433832795

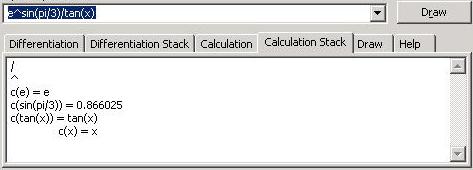
计算堆栈
此视图用于查看计算详细信息的堆栈。c( ) 表示“计算”。堆栈内容从上到下排列。计算步骤是微分步骤,除了运算符公式。此视图的优点是它能够显示可以计算的表达式部分和不能计算的表达式部分,如图中的示例所示。
绘图
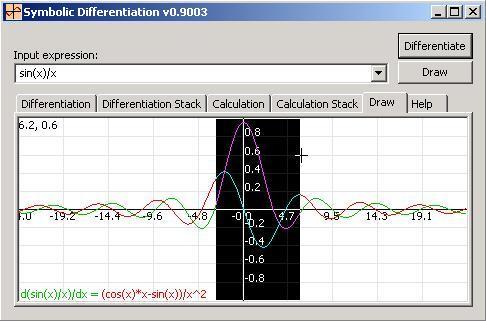
此选项卡用于查看输入函数曲线及其导数曲线。您可以通过单击“绘图”来仅查看输入函数曲线。视图包括水平和垂直轴以及网格线。当您将鼠标移到视图中的任何点上时,左上角会显示其坐标,您可以通过鼠标选择任何部分来放大。水平和垂直轴的限制会自动更新以包含视图中的输入函数点。您可以通过右键单击视图来更改这些限制。
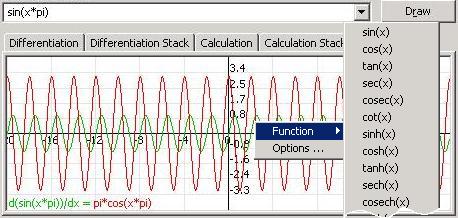
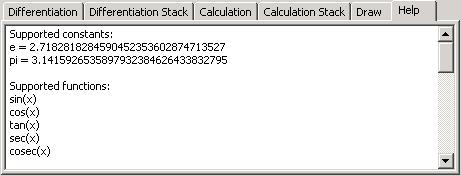
帮助
此选项卡仅显示应用程序中允许的函数列表。
兴趣点
- 部分表达式计算
我的表达式解析优于网络上其他解析器的一点是,它可以计算部分表达式而保留另一部分,这包括任何变量。例如,取表达式
sin(45+sin(2))/tan(x)。如果您尝试将此表达式输入到网络上的任何免费解析器,它会给出错误,指示无效字符x。然而,我的解析器会给出0.937227/tan(x)。对于任何复杂的表达式,我的解析器会尝试在微分之前优化表达式,并计算任何可以计算的部分。因此,sin(45+sin(2))/tan(x)的微分是(-0.937227*sec(x)^2)/(tan(x))^2。 - 运算符优先级
当一个复杂表达式有多个运算符时,运算符优先级决定了执行运算的顺序。执行顺序会显著影响结果值。运算符具有这些优先级级别。较高级别的运算符在较低级别的运算符之前求值。
- +(正号),-(负号)
- ^(指数),%(模)
- *(乘法),/(除法)
- +(加法),-(减法)
当表达式中的两个运算符具有相同的运算符优先级级别时,它们将根据它们在表达式中的位置从左到右进行求值。例如,在
4 - 2 + 27中,减法运算符在加法运算符之前求值,得到2 + 27,其表达式结果为29。使用括号覆盖表达式中运算符的定义优先级。括号内的所有内容都将首先求值,得出单个值,然后才能由括号外的任何运算符使用。例如,
2 * 4 + 5求值为8 + 5,表达式结果为13。表达式2 * (4 + 5)求值为2 * 9;括号导致加法首先执行,因此表达式结果为 18。如果表达式包含嵌套括号,则首先求值最深嵌套的表达式。例如
2 * (4 + (5 - 3) )包含嵌套括号,其中表达式5 - 3在最深嵌套的括号集中。此表达式的值为2。然后加法运算符(+)将此结果与4相加,得到值6。最后,将6乘以2,得到表达式结果12。 - 放大
在绘图区域,您可以选择任何区域进行放大。例如,函数
sin(100*x)具有非常大的变化,如下图所示
通过多次放大,我们可以查看更小的细节,如下图所示



注意:每次放大后请检查水平轴分辨率。
更新
- v0.9001:添加了函数参数的错误检查
- v0.9002:添加了指数导数和一些方程优化,
d(u^v) = v*u^(v-1)*du+u^v*ln(u)*dv - v0.9003:修复了
sec、cosec、sech和cosech函数定义不正确的错误 - v0.9004:添加了软件许可部分
- v0.9005:d(cosh(x))/dx = sinh(x),感谢“Mike O'Neill”
- v0.9006:修正了atan函数计算,感谢“Kevin”
- v0.9007:调整了方程优化函数。感谢“Kevin”
- v0.90071:[2008年5月3日] 调整了方程优化函数。感谢“Kevin”
参考文献
- 高级数学(面向工程师和科学家),作者:Murray R. Spiegel, Ph.D. 1983(微分公式)
- Microsoft Developer Network(运算符优先级)
