迭代快速一维正向 DCT

• 下载 Test_Fast_DCT - 1.02 MB
• 下载 DCT - 1.56 KB

引言

离散余弦变换 (DCT) 是一种广为人知的变换。它具有非常广泛的应用，并用于压缩、处理等，这归功于其系数的实数特性。DCT 的使用频率比傅里叶变换更高。但对于 DCT，只有一种快速算法是众所周知的——用于二维处理。对于一维 DCT，存在 Byeong Lee 的 DCT 算法。但它的算法是递归的。对于某些类型的设备（例如 GPGPU），使用它没有意义。为此，我创建了一个迭代算法，没有递归调用，并且几乎可以处理无限的输入数据（仅为 2 的幂）。

背景

基础选择了 Byeong Lee 的 DCT，如图所示。该算法基于蝴蝶分布。该算法广泛用于硬件实现。

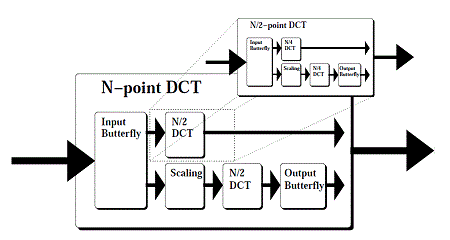
Using the Code

开发的代码基于两个路径：输入路径使用输入蝴蝶，输出路径使用输出蝴蝶。

用于在迭代之间存储数据的数组只有一个，并且按需从堆中分配。另一个数组用于存储计算出的余弦系数。每次迭代都会将前缓冲区分成两部分：偶数和奇数。在将它们复制到后缓冲区后，前缓冲区和后缓冲区会交换位置。

//
double *Front, *Back, *temp; // Pointers on Front, Back, and temp massives of iteration.
double *Array = new double[N<<1]; // Massive with doubling size. 
double *Curent_Cos = new double[N>>1]; // store for precomputing.

Front = Array; // Front pointed on begin Massive.
step = 0;
Back = Front + N; // Back pointed on center of Massive.
        
for(i = 0; i < N; i++)
{
    Front[i] = block[i]; // Load input Data
}

while(j > 1)// Cycle of iterations Input Butterfly
{
    half_N = half_N >> 1;
    current_PI_half_By_N = PI_half / (double)prev_half_N;
    current_PI_By_N = 0;
    step_Phase = current_PI_half_By_N * 2.0;
    for(i = 0; i < half_N; i++)
    {
        //Precompute Cosine's coefficients
        Curent_Cos[i] = 0.5 / cos(current_PI_By_N + current_PI_half_By_N);
        current_PI_By_N += step_Phase;
    }
    shif_Block = 0;
    for(int x = 0; x < step; x++)
    {    
        for(i= 0; i<half_N; i++)
        {
            shift = shif_Block + prev_half_N - i - 1;
            Back[shif_Block + i] = Front[shif_Block + i] + Front[shift];

            Back[shif_Block + half_N + i] = 
              (Front[shif_Block + i] - Front[shift]) * Curent_Cos[i];
        }
        shif_Block += prev_half_N;
    }
    temp = Front;
    Front = Back;
    Back = temp;
    j = j >> 1;
    step = step << 1;
    prev_half_N = half_N;
}      

while(j < N) // Cycle of Out ButterFly
{
    shif_Block = 0;
    for(int x = 0; x < step; x++)
    {     
        for(i = 0; i<half_N - 1; i++)
        {
            Back[shif_Block + (i << 1)] = Front[shif_Block + i];    
            Back[shif_Block + (i << 1) + 1] = 
               Front[shif_Block + half_N + i] + Front[shif_Block + half_N + i + 1];    
        }
        Back[shif_Block + ((half_N - 1) << 1)] = Front[shif_Block + half_N - 1]; 
        Back[shif_Block + (half_N << 1) - 1] = Front[shif_Block + (half_N << 1) - 1]; 
        shif_Block += prev_half_N;
    }
    temp = Front;
    Front = Back;
    Back = temp;
    j = j << 1;
    step = step >> 1;
    half_N = prev_half_N;
    prev_half_N = prev_half_N << 1;
}
for(int i = 0; i < N; i++)
{
    block[i] = Front[i]; // Unload DCT coefficients 
}
block[0] = block[0] / dN; // Compute DC.

关注点

一个非常重要的事实是，在第一次迭代之后，我们只有一个奇数系数组，但在第二次迭代之后，我们有两个奇数系数组。对于这两个组，您需要相同的余弦系数。存储预计算结果允许仅为一组计算该系数。对于另一组，将使用存储中的数据。这对于计算 1024 个或更多点非常有用。

最后，我可以说，由于减少了余弦系数的计算，开发的算法比常规实现具有更高的精度。

历史

• 2011年1月27日：初始发布