2D 多边形碰撞检测

• 下载演示项目 - 7.44 Kb
• 下载源代码 - 15.1 Kb

引言

本文介绍如何检测两个移动的（2D）多边形之间的碰撞。 这不是第一个关于该主题的教程，但是，网络上的教程对于一个相对简单的问题来说往往过于复杂。 我能找到的源代码也有太多的缩写，我看不懂，或者充满了 C 优化。 所以在这里，我将尽量保持简单。 在任何情况下，应该可以将此处提供的函数直接包含到您的 C# 项目中。 该技术可用于检测精灵之间的碰撞，作为像素完美碰撞的替代方法，后者通常太慢。

背景

为了检测两个多边形是否相交，我们使用分离轴定理。 这个想法是找到一条分离两个多边形的线 - 如果存在这样一条线，则多边形不相交（图 1）。 这个定理的实现相对简单，可以总结为以下伪代码

• 对于两个多边形的每一条边
  • 找到垂直于当前边的轴。
  • 将两个多边形投影到该轴上。
  • 如果这些投影不重叠，则多边形不相交（退出循环）。

通过添加一个额外的步骤，可以很容易地扩展到处理移动的多边形。 在检查当前投影没有重叠之后，将多边形的相对速度投影到轴上。 通过将速度投影添加到第一个多边形，来扩展第一个多边形的投影（图 2）。 这将为您提供多边形在运动期间跨越的间隔。 从那里，您可以使用用于静态多边形的技术：如果多边形 A 和 B 的投影不重叠，则多边形不会发生碰撞。（注意：但是，请记住，如果间隔确实重叠，这并不一定意味着多边形会碰撞。 我们需要对所有边进行测试才能知道这一点。）

一旦我们发现多边形将要碰撞，我们计算将多边形推开所需的平移量。 投影重叠最小的轴将是发生碰撞的轴。 我们将沿该轴推动第一个多边形。 然后，平移量将简单地是在该轴上的重叠量（图 3）。

就是这样！ 现在，每次发生碰撞时，第一个多边形都会很好地沿着另一个多边形的表面滑动。

图 1： 多边形在轴上的投影。

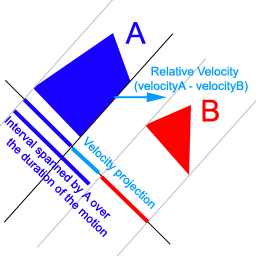
图 2： 移动多边形的投影。

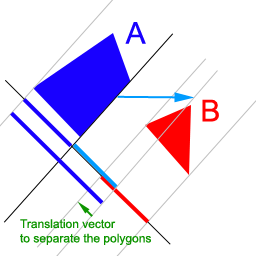
图 3： 找到最小的间隔重叠，然后计算将多边形推开所需的平移量。

使用代码

PolygonCollision() 函数执行以上所有操作，并返回一个 PolygonCollisionResult 结构，其中包含处理碰撞所需的所有必要信息

// Structure that stores the results of the PolygonCollision function
public struct PolygonCollisionResult {
    // Are the polygons going to intersect forward in time?
    public bool WillIntersect;
    // Are the polygons currently intersecting?
    public bool Intersect;
    // The translation to apply to the first polygon to push the polygons apart.
    public Vector MinimumTranslationVector;
}

PolygonCollision 函数使用了两个辅助函数。 第一个用于将多边形投影到轴上

// Calculate the projection of a polygon on an axis
// and returns it as a [min, max] interval
public void ProjectPolygon(Vector axis, Polygon polygon, 
                           ref float min, ref float max) {
    // To project a point on an axis use the dot product
    float dotProduct = axis.DotProduct(polygon.Points[0]);
    min = dotProduct;
    max = dotProduct;
    for (int i = 0; i < polygon.Points.Count; i++) {
        dotProduct = polygon.Points[i].DotProduct(axis);
        if (d < min) {
            min = dotProduct;
        } else {
            if (dotProduct> max) {
                max = dotProduct;
            }
        }
    }
}

第二个返回两个给定投影之间的有符号距离

// Calculate the distance between [minA, maxA] and [minB, maxB]
// The distance will be negative if the intervals overlap
public float IntervalDistance(float minA, float maxA, float minB, float maxB) {
    if (minA < minB) {
        return minB - maxA;
    } else {
        return minA - maxB;
    }
}

最后，这是主函数

// Check if polygon A is going to collide with polygon B.
// The last parameter is the *relative* velocity 
// of the polygons (i.e. velocityA - velocityB)
public PolygonCollisionResult PolygonCollision(Polygon polygonA, 
                              Polygon polygonB, Vector velocity) {
    PolygonCollisionResult result = new PolygonCollisionResult();
    result.Intersect = true;
    result.WillIntersect = true;

    int edgeCountA = polygonA.Edges.Count;
    int edgeCountB = polygonB.Edges.Count;
    float minIntervalDistance = float.PositiveInfinity;
    Vector translationAxis = new Vector();
    Vector edge;

    // Loop through all the edges of both polygons
    for (int edgeIndex = 0; edgeIndex < edgeCountA + edgeCountB; edgeIndex++) {
        if (edgeIndex < edgeCountA) {
            edge = polygonA.Edges[edgeIndex];
        } else {
            edge = polygonB.Edges[edgeIndex - edgeCountA];
        }

        // ===== 1. Find if the polygons are currently intersecting =====

        // Find the axis perpendicular to the current edge
        Vector axis = new Vector(-edge.Y, edge.X);
        axis.Normalize();

        // Find the projection of the polygon on the current axis
        float minA = 0; float minB = 0; float maxA = 0; float maxB = 0;
        ProjectPolygon(axis, polygonA, ref minA, ref maxA);
        ProjectPolygon(axis, polygonB, ref minB, ref maxB);

        // Check if the polygon projections are currentlty intersecting
        if (IntervalDistance(minA, maxA, minB, maxB) > 0)\
            result.Intersect = false;

        // ===== 2. Now find if the polygons *will* intersect =====

        // Project the velocity on the current axis
        float velocityProjection = axis.DotProduct(velocity);

        // Get the projection of polygon A during the movement
        if (velocityProjection < 0) {
            minA += velocityProjection;
        } else {
            maxA += velocityProjection;
        }

        // Do the same test as above for the new projection
        float intervalDistance = IntervalDistance(minA, maxA, minB, maxB);
        if (intervalDistance > 0) result.WillIntersect = false;

        // If the polygons are not intersecting and won't intersect, exit the loop
        if (!result.Intersect && !result.WillIntersect) break;

        // Check if the current interval distance is the minimum one. If so store
        // the interval distance and the current distance.
        // This will be used to calculate the minimum translation vector
        intervalDistance = Math.Abs(intervalDistance);
        if (intervalDistance < minIntervalDistance) {
            minIntervalDistance = intervalDistance;
            translationAxis = axis;

            Vector d = polygonA.Center - polygonB.Center;
            if (d.DotProduct(translationAxis) < 0)
                translationAxis = -translationAxis;
        }
    }

    // The minimum translation vector
    // can be used to push the polygons appart.
    if (result.WillIntersect)
        result.MinimumTranslationVector = 
               translationAxis * minIntervalDistance;
    
    return result;
}

该函数可以这样使用

Vector polygonATranslation = new Vector();

PolygonCollisionResult r = PolygonCollision(polygonA, polygonB, velocity);

if (r.WillIntersect) {
  // Move the polygon by its velocity, then move
  // the polygons appart using the Minimum Translation Vector
  polygonATranslation = velocity + r.MinimumTranslationVector;
} else {
  // Just move the polygon by its velocity
  polygonATranslation = velocity;
}

polygonA.Offset(polygonATranslation);

参考

• GPWiki - 多边形碰撞
• Olivier 的代码垃圾场

历史

• 2006 年 9 月 13 日：第一个版本。
• 2006 年 9 月 14 日：小的更改，并添加了参考部分。