堆数据结构

• 下载源代码 - 1.23 KB

引言

本文简要描述了堆数据结构的概念，并提供了实现源代码 - CHeapTree 类。CHeapTree 是一个基于数组的自动调整大小的类，它高效地实现了堆数据结构。

什么是堆

堆是一种数据结构，是一种特殊的完全二叉树。 主要区别在于堆以部分排序的方式存储其节点。 此外，节点是从左到右填充的，因此如果特定节点没有左子节点，它也不应该有右子节点。 此外，如果h层有一个节点，则h - 1层应该被满足。

以下是堆的正式定义 [来自 S. Baase 和 A. Van Gelder 的《计算机算法》]

当且仅当二叉树 V 满足以下条件时，它才是堆结构

1. V 至少通过深度 h - 1 是完整的
2. 所有叶子都在深度 h 或 h - 1 处
3. 通向深度 h 的叶子的所有路径都在通向深度 h - 1 的叶子的所有路径的左侧

堆有两种 - 最小堆和最大堆。 最小堆是一个堆，其中每个节点的优先级小于或等于其子节点的优先级。 最大堆是一个堆，其中每个节点的优先级大于或等于其子节点的优先级。

最大堆 (左) 和最小堆 (右) 的示例

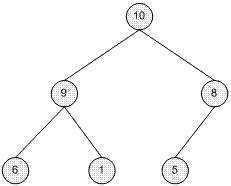
基本实现细节

类 CHeapTree 通过一个数组来实现堆结构，其中节点通过从上到下、从左到右读取树来存储。 因此，上面的最大堆将是：10、9、8、6、1、5。 在这种表示中，第 j 个索引的子节点和父节点可以按如下方式标识 [假设从零开始索引]

• 左子节点索引 = j * 2 - 1
• 右子节点索引 = j * 2 = 左子节点索引 + 1
• 父节点索引 = (j - 1) / 2

如果任何索引超出数组的边界，则该节点不存在。

成本

• 堆构造完成的键比较次数：O(n)
• 堆删除完成的键比较次数：2*n*lg(n)
• 堆排序在平均和最坏情况下的比较次数：BigTheta(n*lg(n) )

CHeapTree 声明（详细信息省略）

template <class TID, class TDATA>
class CHeapTree
{
    struct _NODE {
        TID id;
        TDATA data;
    };
    _NODE *m_data;

public:
    CHeapTree(int nInitMax = 100);
    ~CHeapTree();

    bool IsEmpty() const { return m_nSize == 0; }
    int GetSize() const { return m_nSize; }

    void Insert(const TID &id, const TDATA &data);
    bool RemoveTop();
    bool RemoveAll();

    bool GetTopID(TID *pid) const;
    bool GetTopData(TDATA *pdata) const;
    bool GetData(const TID &id, TDATA *pdata) const;

    bool ResetData(const TID &id, const TDATA &data);

private:
    void _ReformatHeap(int iRoot);
};

该类实现了堆的基本操作。 在 CHeapTree 中，数据排序基于 TDATA 类型的值进行。 因此，如果您的 TDATA 是用户定义的类型，则它应该具有 <、= 和 > 运算符重载。 比较的逻辑由用户决定。 TID 是一个代表值，使得每个节点都可以通过其 TID 值唯一标识。 如果没有，则排序顺序未定义。

默认情况下，CHeapTree 是一个最小堆。 也就是说，TDATA 的较低值具有更高的优先级。 要使其成为最大堆，您应该更改 [反转] TDATA 类型的比较运算符的逻辑。

如何使用

使用这个类非常简单。 可能是这样的

// int=id, float=priority [as less as better]

CHeapTree<int, float> h;
h.Insert(0, 0.1f);
h.Insert(1, 0.2f);
h.Insert(2, 0.15f);
h.Insert(3, 0.3f);
h.Insert(4, 0.21f);

h.ResetData(3, 0.19f);
// The order should be [0, 2, 3, 1, 4]


while (!h.IsEmpty()) {
    int top;
    h.GetTopID(&top); 
    float data;
    h.GetTopData(&data); 
    cout << "(" << top << " : " << data << ")\n";
    h.RemoveTop();
}

结束

您可以在此页面上找到 CHeapTree 类。 如果您有建议和笔记，请随时与我分享。

编程愉快！