一些简单的 C++ 数值方法
4.97/5 (18投票s)
为初学者介绍数值方法入门文章。

引言
本文旨在让初学者熟悉数值方法。我在数值分析和方法方面做了很多工作,我想与您分享我的一些经验和遇到的结果。这是“数值分析方法及其在 C++ 中的实现”系列文章的第一篇。
读完本文后,您可能会想“为什么要重复造轮子?”。当然,互联网上有很多关于此处讨论问题的参考文献,但我的目的不是重复造轮子,而是试图详细解释数值分析中的一些经典方法,它们的作用、用途、实现方式,以及最重要的是,如何使用它们。
在本文中,我们将重点关注数学中的两个著名方程,它们在几乎所有科学领域都具有巨大的重要性:F(x) = 0 和 F(x) = x。数学、化学、物理中的许多问题都归结为求解这两个方程之一,这就是为什么历代科学家都努力提供解决这些方程的良好方案。我们将介绍一些尝试求解这些方程的数值方法,并尝试对这些方法进行简短分析,展示每种方法的优缺点。
方法及其实现
我们文章的第一项内容是求解方程 F(x) = 0 的问题,其中 F(x) 可以是任何类型的函数。例如,我们可以有 F(x) = x^2 + 6x + 6,或者 F(x) = cos(x)。这是数学中一个众所周知的问题,而且我们也知道,没有办法精确地找到所有这类方程的解。因此,数学家们一直在努力为这个方程提供近似解。请注意,方程 F(x) = 0 的解通常被称为函数 F(x) 的根。
牛顿法
牛顿法的思路是这样的:我们从一个初始解值(也称为初始近似值)开始,然后用函数的切线代替函数,并计算该切线的根,这将是函数根的更好近似值。我们重复此过程,直到找到一个合适的解(一个足够接近实际解并且非常符合方程 F(x) = 0 的解)。显然,这个过程实际上是一个迭代过程。另外请注意,为了应用牛顿算法,函数 F 必须是实值可微函数。
具体来说,如果我们有一个当前近似值 xCrt,那么下一个近似值 nNxt 将使用以下公式计算
xNxt = xCrt - (F(xCrt) / F`(xCrt))
其中 F` 表示函数 F 的导数。迭代过程将在达到最大允许的迭代次数仍找不到解时停止,或者在找到一个足够接近方程实际解的近似值时停止。下面是实现牛顿法的代码
/*
* Newton's method for solving equation F(x) = 0
* Output:
* x - the resulted approximation of the solution
* Return:
* The number of iterations passed
*/
int NewtonMethodForEquation(double& x)
{
int n = 1;
while( ( fabs(F(x)) > error ) && ( n <= MAXITER ) )
{
x = x - ( F(x) / Fd(x) );
n++;
}
return n;
}
在上面的代码片段中,Fd 表示函数 F 的导数。
割线法
割线法是求解方程 F(x) = 0 的另一种方法。该方法几乎与牛顿法相同,不同之处在于我们在开始迭代过程之前选择两个初始近似值而不是一个。假设我们有当前的近似值 xCrt0 和 xCrt1。这次将使用以下公式计算下一个近似值 xNxt
xNxt = xCrt1 - (F(xCrt1)(xCrt1 - xCrt0)) / (F(xCrt1) - F(xCrt0))
请注意,与牛顿法一样,此方法不需要函数 F 的导数。下面是实现割线法的代码
/*
* Secant method for solving equation F(x) = 0
* Input:
* x0 - the first initial approximation of the solution
* x1 - the second initial approximation of the solution
* Output:
* x - the resulted approximation of the solution
* Return:
* The number of iterations passed
*/
int SecantMethodForEquation(double& x, double x0, double x1)
{
int n = 2;
while( ( fabs(F(x1)) > error ) && ( n <= MAXITER ) )
{
x = x1 - (F(x1) * (x1 - x0)) / (F(x1) - F(x0));
x0 = x1;
x1 = x;
n++;
}
return n;
}
有时还会遇到另一个问题,即求解方程 F(x) = x。如果我们这样写方程:F(x) - x = 0,并设 G(x) = F(x) - x,那么方程就变成 G(x) = 0。但是,F(x) = x 形式的方程对数学家来说具有特殊的意义。据说,如果 x0 是方程 F(x) = x 的解,那么 x0 就称为函数 F(x) 的不动点。当然,我们可以将前面学到的方法应用于方程 G(x) = 0,但我们的兴趣在于介绍求解方程 F(x) = x 的方法。
逐次逼近法
这种方法虽然简单,但在数学上却非常重要,被广泛应用于许多不动点理论。让我们看看这种方法是如何工作的。首先,和以前一样,我们选择一个初始近似值 x0,并开始迭代过程。如果 xCrt 表示当前近似值,那么 xNxt 的计算方式如下
xNxt = F(xCrt)
这是一个相当简单的公式,出乎意料的是,已经证明该方法通常会在一定次数的迭代后收敛,从而得到方程解的良好近似值。源代码非常直接
/*
* Successive approximations method for solving equation F(x) = x
* Output:
* x - the resulted approximation of the solution
* Return:
* The number of iterations passed
*/
int SuccessiveApproxForEquation(double& x)
{
int n = 1;
while( ( fabs(x - F1(x)) > error ) && ( n <= MAXITER ))
{
x = F1(x);
n++;
}
return n;
}
这种方法虽然简单有用,但有一个很大的缺点:收敛速度非常慢,也就是说,直到得到解所需的迭代次数会很高。如果选择的初始近似值接近方程的实际解,迭代过程会足够快,算法也能找到合适的解。但是,如果初始近似值是随机选择的,那么过程可能根本找不到解(取决于允许的最大迭代次数,以及初始近似值与实际解的接近程度)。
为了克服这个问题,一些数学家试图加速迭代方法寻找正确解的过程。因此,开发了一些算法来做到这一点(这些算法通常称为收敛加速算法)。最重要的收敛加速算法是艾特肯算法和奥弗霍尔特算法。
收敛加速算法背后的思想是这样的:如果我们仔细观察迭代过程,就会发现如果我们选择每一步的近似值,我们可以形成一个实数序列:x0, x1, x2, ... ,xn,该序列在经过一定次数的迭代后会收敛到方程 F(x) = x 的解 (x)。收敛加速算法将数字序列 x0, x1, x2, ... ,xn 转换为另一个实数序列 y0, y1, y2, ... yn,该序列具有一个非常重要的特性,即它以更快的速度收敛到解 x。
我们在下面的部分介绍三种这样的收敛加速算法,并坚持我们求解方程 F(x) = x 的问题。
艾特肯法
艾特肯法是一种与前面介绍的方法类似的迭代过程。我将不再赘述数学细节。取而代之的是,我更愿意展示艾特肯法的代码
/*
* Aitken's method for solving equation F(x) = x
* Input:
* x0 - the initial approximation of the solution
* Output:
* y - the resulted approximation of the solution
* Return:
* The number of iterations passed
*/
int AitkenMethodForEquation(double& y, double x0)
{
int n = 1;
double x;
do
{
x = F1(x0);
y = x + 1 / ((1 / (F1(x) - x)) - (1 / (x - x0)));
n++;
x0 = x;
}
while((fabs(y - F1(y)) > error) && (n <= MAXITER));
return n;
}
斯蒂芬森法
该方法是艾特肯方法的一个简化版本,通过观察如果我们对值 xCrt, F(xCrt), F(F(xCrt)) 应用艾特肯公式,我们会得到
xNxt = (xCrt F(F(xCrt)) - (F(xCrt)) ^ 2) / (F(F(xCrt)) - 2F(xCrt) + xCrt)
简化形式如下
xCrt = F(xCrt) + 1 / ((1 / (F(F(xCrt)) - F(xCrt))) - (1 / (F(xCrt) - xCrt)))
该算法的代码是
/*
* Steffensen's method for solving equation F(x) = x
* Output:
* x - the resulted approximation of the solution
* Return:
* The number of iterations passed
*/
int SteffensenMethodForEquation(double& x)
{
int n = 0;
do
{
x = F1(x) + 1 / ( (1 / (F1(F1(x)) - F1(x)) ) - (1 / (F1(x) - x) ) );
n++;
}
while((fabs(x - F1(x)) > error) && (n <= MAXITER));
return n;
}
奥弗霍尔特法
奥弗霍尔特法是目前为止求解方程 F(x) = x 最快的方法。我将展示该算法的代码,方法本身从源代码中就可以很容易地理解
/*
* Overholt's method for solving equation F(x) = x
* Input:
* x0 - the initial approximation of the solution
* s - the convergence order (s must be >= 2)
* Output:
* x - the resulted approximation of the solution
* Return:
* The number of iterations passed
*/
int OverholtMethodForEquation(double &x, double x0, int s)
{
int m = 0;
x = x0;
do
{
V[0][0] = x;
for(int n = 1; n <= s; n++)
V[0][n] = F1(V[0][n - 1]);
for(int k = 0; k <= s - 2; k++)
for(int n = 0; n <= s - k - 2; n++)
V[k + 1][n] = (pow(V[0][n + k + 2] - V[0][n + k + 1], k+1) * V[k][n] -
pow(V[0][n + k + 1] - V[0][n + k], k + 1) * V[k][n + 1]) /
(pow(V[0][n + k + 2] - V[0][n + k + 1], k + 1) -
pow(V[0][n + k + 1] - V[0][n + k], k + 1));
m++;
x = V[s - 1][0];
}
while((fabs(x - F1(x)) > error) && (m <= MAXITER));
return m;
}
在上面的源代码中,V 是一个全局变量,声明为
// matrix used in Overholt algorithm
// this is declared as a global variable to avoid stack overflow
double V[100][100];
使用代码
现在,让我们看看如何有效地使用上述方法,并在此过程中对这些方法进行简短分析。
为了使用这些方法,我们首先必须定义一些常量
// the maximum number of iterations
const int MAXITER = 100;
// the accepted error
const double error = 0.0001;
MAXITER 表示算法允许通过的最大迭代次数,这意味着如果我们的算法之一已经通过了 MAXITER 次迭代但仍未找到合适的解,算法仍将停止。error 表示可接受的最小误差,这意味着近似解必须在满足此误差的情况下足够接近方程的真实解。误差值越小,近似解就越接近真实解。
让我们以 x*e^x - 1 = 0 为例,取第一类方程。所以,我们有 F(x) = x*e^x - 1。我们在代码中定义了这个函数,以及它的导数,因为我们将需要它来应用牛顿法
// the Euler constant
const double e = 2.718281828459;
// the function F(x)
#define F(x) ( x * pow(e, x) - 1 )
// the derivative of the function F(x), meaning F`(x)
#define Fd(x) ( (x + 1) * pow(e, x) )
您可以更改函数 F 及其导数 Fd,然后就可以求解您喜欢的任何类型的方程了
double x;
int n;
/* Example usage for Newton Method */
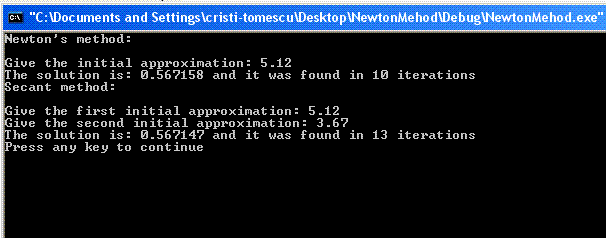
cout << "Newton's method: " << endl << endl;
cout << "Give the initial approximation: ";
cin >> x;
// now we apply Newton's method
n = NewtonMethodForEquation(x);
if(n > MAXITER)
cout << "In " << MAXITER << " iterations no solution was found!" << endl;
else
cout << "The solution is: " << x << " and it was found in "
<< n << " iterations" << endl;
double x0, x1;
/* Example usage for Secant Method */
cout << "Secant method: " << endl << endl;
cout << "Give the first initial approximation: ";
cin >> x0;
cout << "Give the second initial approximation: ";
cin >> x1;
// now we apply the Secant method
n = SecantMethodForEquation(x, x0, x1);
if(n > MAXITER)
cout << "In " << MAXITER << " iterations no solution was found!" << endl;
else
cout << "The solution is: " << x << " and it was found in "
<< n << " iterations" << endl;
现在,您可以尝试使用这些算法,给出各种初始近似值,并减小或增大 error 值来观察它们的行为。我们可以看到,总体而言,牛顿法比割线法快。
对于第二类方程,让我们以 F(x) = e^(-x) 为例,方程变为 e^(-x) = x。
#define F1(x) ( pow(e, -x) )
下面是我们应用算法的方法
/* Example usage for Successive Approximations Method */
cout << "Successive approximations method: " << endl << endl;
cout << "Give the initial approximation: ";
cin >> x;
n = SuccessiveApproxForEquation(x);
if(n > MAXITER)
cout << "In " << MAXITER << " iterations no solution was found!" << endl;
else
cout << "The solution is: " << x << " and it was found in "
<< n << " iterations" << endl;
/* Example usage for Aitken Method */
cout << "Aitken's method: " << endl << endl;
cout << "Give the initial approximation: ";
cin >> x;
double y;
n = AitkenMethodForEquation(y, x);
if(n > MAXITER)
cout << "In " << MAXITER
<< " iterations no solution was found!" << endl;
else
cout << "The solution is: " << y << " and it was found in "
<< n << " iterations" << endl;
/* Example usage for Steffensen Method */
cout << "Steffensen's method: " << endl << endl;
cout << "Give the initial approximation: ";
cin >> x;
n = SteffensenMethodForEquation(x);
if(n > MAXITER)
cout << "In " << MAXITER
<< " iterations no solution was found!" << endl;
else
cout << "The solution is: " << x << " and it was found in "
<< n << " iterations" << endl;
/* Example usage for Overholt Method */
cout << "Overholt's method: " << endl << endl;
cout << "Give the initial approximation: ";
cin >> x;
double rez;
n = OverholtMethodForEquation(rez, x, 2);
if(n > MAXITER)
cout << "In " << MAXITER
<< " iterations no solution was found!" << endl;
else
cout << "The solution is: " << rez << " and it was found in "
<< n << " iterations" << endl;
尝试也玩玩这些算法,您会发现,事实上,奥弗霍尔特法是求解 F(x) = x 型方程的稳定且快速的方法。
最后的话
在本文中,我试图向您介绍数学中最著名且最有用的两个方程,它们在 IT 领域也非常有用,并尝试介绍一些数值算法来求解它们,这些算法非常容易理解,并且在您的应用程序中也非常容易使用。
历史
目前还没有。
