Pegboard 解决方案

• 下载源代码 - 17.3 KB

问题陈述

我在 1997 年在必胜客等披萨时遇到了钉板问题。它是一个有 15 个孔的三角形板，除了一个孔外，每个孔都有一个钉子。

你可以将一个钉子跳过另一个钉子，前提是：有一个钉子可以被跳过，并且有一个孔可以被跳过去。你不断移动钉子，直到板上只剩下一个钉子。

蒙特卡洛模拟

我们都可以最终解决这个问题：通过纯粹的试错法，或者通过稍微思考最终结果并倒推等等。

披萨吃完后，我回到家，写了一个简单的 C 代码来解决这个问题的所有变体（针对所有初始空孔的位置）。该代码本质上执行试错方法，但速度更快。它知道板的初始状态和最终状态，并尽可能移动钉子。然后，代码会检查当钉子无法再移动时的结果。如果板上只剩下一个钉子，则谜题解决，并将显示达到该状态的步骤。如果板上剩余的钉子多于一个，则程序将从初始状态重新开始该过程。在几秒钟和数百次迭代之后，解决方案就会显示出来。

这种模拟方法并非新鲜事物。“蒙特卡洛”一词由约翰·冯·诺依曼创造，他曾负责回答这个问题：“原子弹爆炸时世界会因链式反应而被摧毁吗？”。这至少是一个非常复杂的问题。亚原子粒子的路径以及可能因此发生的反应都使得这个问题成为一个开放系统，即无法通过已知的数学程序精确求解。因此需要通过快速机器进行模拟。冯·诺依曼实际上帮助宾夕法尼亚大学的人们创建了一台具有进行此类模拟所需所有规格的计算机：软件驻留在内存中并一次又一次地重播，同时存储结果。时至今日，大多数计算机都利用了冯·诺依曼架构。

相似但更简单的手动模拟也启发了冯·诺依曼。其中最著名的一种早期模拟被称为“蒲丰投针问题”，即针落在一个由平行木条构成的地板上，以及它们与两条木条之间线相交的观察频率最终导致对 π 的近似。这是 18 世纪法国人乔治-路易·勒克莱尔（Comte de Buffon）的工作。

钉板问题有精确的解决方案和确切的步骤，这使其成为一个“封闭”系统。通过蛮力技术也可以在合理的时间内解决这个问题。在我看来，编写一个模拟程序更容易，因为我不必对整个游戏空间进行详尽的考察。动态规划无疑也是解决这个谜题的一种巧妙方法。

软件的总体结构

PEGSOLVE.cpp 是用 Borland C++ 3.1 编写的，最近我使用 gcc C++ 4.x 测试了代码。其编程风格属于“游戏”类型，不使用 STL 等强大的 C++ 库。

定义范围

代码的第一部分使用一个数组 `static int orig_pegboard[15]` 来定义系统范围，该数组代表钉板。这在每次迭代开始时都会被反复使用。

定义元素

系统中主要的“角色”是钉子，它可以四处移动。

定义行为

由于一次移动包含三个元素，因此定义了一个 `_move_set` 结构，其中包含要移动的钉子、第一个钉子移动时被移除的钉子，以及第一个钉子的新位置。

定义规则

对于特定孔中的每个钉子，都有一套完整的、可能可行或不可行的移动。这组移动由一个名为 `peg_move_rules` 的数组表示。

在约束范围内根据一套规则行事的实体构成了系统。在这个系统之外，我们提取出我们需要的东西：钉板问题的解决方案。我们识别出钉板的一种状态，即实际上是解决方案，而所有为达到解决方案而发生的事件（钉子移动）就是我们所需要的。

上面定义的所有内容现在都将在计算机应用程序的运行时使用，以下是伪代码：

While (the pegboard is not solved) 
{ 
    Reset to the original state of the pegboard. 
    Reset all move traceability. 
    Get all the possible moves that can be made 
        at the current state of the pegboard. 
    While (there is a move that can be made) 
    { 
        Pick a move and just do it. 
        Keep a track of this move. 
        Get all the possible moves that can be made 
            at the current state of the pegboard. 
    } 
} 

就是这样。

结果

我将在此处展示一个问题的结果。假设初始状态是第一个孔为空。如果您运行“pegsolve.exe 1”，输出将是：

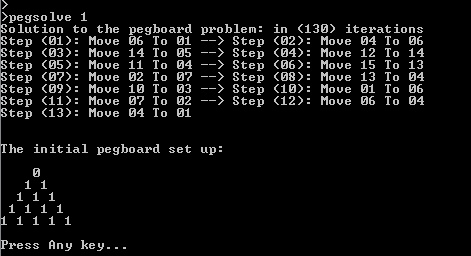
该解决方案在 130 次迭代中达到。

偏置随机数生成器的 PDF

均匀分布的随机数生成确保了任何生成数字的概率相等；即，1 到 10 之间的数字“2”的概率（0.1）与“6”的概率相同。

但为什么随机数生成应该是均匀分布的呢？因为否则将需要更多工作。然而，人们有理由认为，最终钉子数较少的移动序列比钉子数较多的移动序列更好。也许，那么，一些移动可以在随机选择中被赋予比其他移动更重的权重——尽管不再是均匀分布——可以比重复过去的错误迭代更快地找到解决方案。根据我几年前上的一门人工智能课的教授的说法，这种解决方案不再被称为蒙特卡洛模拟，因为它每次迭代都不是从 the proverbial “clean slate”（字面意思：干净的石板，比喻：全新的开始）开始的。这是一种遗传算法。

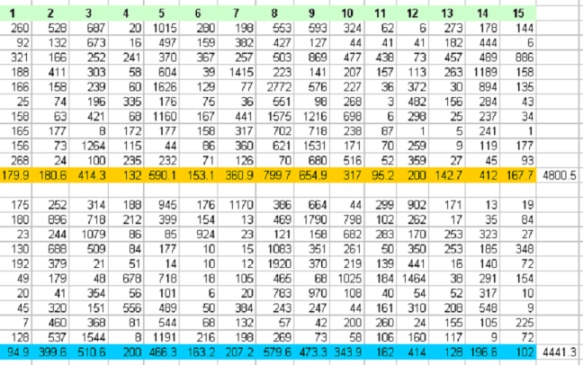
比较两种结果

下面是蒙特卡洛和“偏置蒙特卡洛”的两个结果表。每个列标题代表钉板上的空孔编号，表格中的值代表解决钉板谜题所需的迭代次数。橙色和蓝色条是迭代次数的平均值。最右边的列包含迭代次数的总和。

虽然对于第 1 号孔存在明显的统计差异和改进，但总体性能（考虑所有孔）提高了 7% 以上。对于近一半的孔，迭代次数没有改进（实际上更差）。我无法断定哪种方法更好；但它们是不同的。

历史

• 2007 年 4 月 18 日：初次发布