艺术画廊问题：多边形三角剖分与 3 着色

• 下载演示项目 - 257.3 KB
• 下载源文件 - 313.1 KB

引言

来自 维基百科

艺术画廊问题或博物馆问题是计算几何中一个经过充分研究的可见性问题。该问题的动机是现实世界中用最少数量的可以旋转以获得完整视野的安全摄像机来守护艺术画廊的问题。在该问题的计算几何版本中，艺术画廊的布局由一个简单多边形表示，每个安全摄像机由多边形中的一个点表示。如果对于多边形中的每个点 p，都存在某个 使得 p 和 q 之间的线段不离开多边形，则称点集 S 守护多边形。

正如在我计算图形学课程中所要求的那样，我被要求实现上述艺术画廊问题的解决方案程序。因此，通过使用剪耳三角剖分和3着色算法，我在截图中的实现了上述程序。

背景

读者需要具备计算几何（多边形、点等）的基本知识。

理论

Two-Ears

简单多边形 P 的主顶点 pi 称为一个耳，如果连接 pi 的对角线 (pi-1, pi+1) 完全位于 P 中。如果耳 pi 和 pj 不重叠，则称它们不重叠，即三角形 (pi-1, pi, pi+1) 的内部不与三角形 (pj-1, pj, pj+1) 的内部相交。

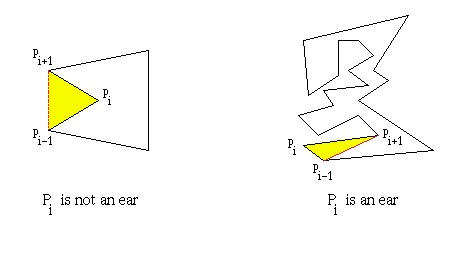
注意：程序代码使用 fgshen 的“C# 中的多边形三角剖分”（https://codeproject.org.cn/csharp/cspolygontriangulation.asp）作为骨架三角剖分代码。有关三角剖分和二耳定理的更多信息，请查阅该页面。

3-着色

图 3-着色是指为图中的每个节点着色（红、绿或蓝），并满足边两端的节点颜色必须不同的约束。

使用代码

基本上，该代码是使用 Visual Studio 2005 和 C# 开发的。代码使用了
System.Drawing 库来处理大部分绘图和计算几何。

这是代码的类列表。

Triangulation - triangulate()*

处理二耳定理三角剖分算法。

public void triangulate()   // triangulate the bigger polygon-shape
{
    mPolygon poly = new mPolygon(updated_vertices); 
                    // create a polygon from the current vertices
        Boolean finished = false; // triangulation-finished?

        if (updated_vertices.Length == 3) 
                    // if there's only 3 points, no need to run algorithm
            finished = true;

        Point p = new Point();

        while (finished == false)   
                    // loop while triangulation not finished yet
        {
        int i = 0;
                Boolean not_found = true;   
                        // did we found an ear? no, not yet
                while (not_found && (i < updated_vertices.Length)) 
                        // while we did not found any ear and 
                        // not yet processed all vertices
                {
                    p = updated_vertices[i];    // get current point
                    if (is_ear(p))              
                        // check if we can get an ear from that vertice
                        not_found = false;      // good we found one
                    else
                        i++;                    // continue to search
                }

                update_vertices(p);             
                    // remove the vertice we found the ear 
                    // from the updated_vertices list
                poly = new mPolygon(updated_vertices);  
                    // reupdate the polygon from the rest of vertices
                if (updated_vertices.Length == 3)   
                    // if there's only 3 vertice left
                    finished = true;                
                    // this means we finished the triangulation
    }

    // when the CS:IP reaches here, this means triangulation finished
    polygons = new Point[ears.Count + 1][]; 
                    // init polygons structure to ears.count + 
                    // 1(for last 3 points left)
    for (int i = 0; i < ears.Count; i++)
    {
        Point[] points = (Point[])ears[i];  
                    // move ears to final triangulated polygons list
                polygons[i] = new Point[3];
                polygons[i][0] = points[0];
                polygons[i][1] = points[1];
                polygons[i][2] = points[2];
            }

                // we have 3 left vertices on updated_vertices list, 
                //    - the last triangulated polygon -
            polygons[ears.Count] = new Point[updated_vertices.Length]; 
                // add it to triangulated polygons list also
            for (int i = 0; i < updated_vertices.Length; i++)
            {
                polygons[ears.Count][i] = updated_vertices[i];
            }
}

Triangulation - is_ear()*

检查给定点是否位于一个有效的耳中。

private Boolean is_ear(Point p) // checks if given vertice is in a ear
{
    mPolygon m = new mPolygon(updated_vertices); 
                    // init. a polygon from the current vertices

    if (m.is_vertex(p) == true) // if given point is a vertex
    {
        if (m.vertex_type(p) == VertexType.ConvexPoint) 
                    // and it's a convex point
                {
                    Point curr_point = p;
                    Point prev_point = m.get_prev_point(p); 
                    // find previous adjacent point
                    Point next_point = m.get_next_point(p); 
                    // find next adjacent point

                    for (int i = updated_vertices.GetLowerBound(0); 
                    i < updated_vertices.GetUpperBound(0); i++) 
                            // loop through all other vertices
                    {
                        Point pt = updated_vertices[i];
                        if (!(is_points_equal(pt, curr_point) || 
                          is_points_equal(pt, prev_point) || 
                          is_points_equal(pt, next_point)))
                        {       // if pt is not equal to checked vertice or 
                            // its's next and prev adjacent vertices
                            if (is_point_in_triangle(new Point[] 
                        { prev_point, curr_point, next_point }, pt)) 
                            // check pt lies in triangle
                                return false;   
                            // if another vertice lies in this 
                            // triangle, then this is not an ear
                        }
                    }
                }
                else         // concave
                    return false; 
                            // we cannot make ears from concave points

                return true;    // if CS:IP reaches here, this means 
                            // vertice passed the test and is an ear
    }
    return false;             // if the given vertex is not an vertex, 
                            // it's not related to an ear also!
}

3-Coloring - traverse()

3着色算法的启动点。为最后一个处理的多边形着色，并调用深度优先着色算法。

public void traverse() // travers the triangulated polygons list for 
            // assigning 3-colors
{
    int last_poly = polygons.Length - 1; // find last polygon on list
    lb.Items.Add("[p" + last_poly + "] Last Polygon: \t" + 
        polygons[last_poly][0] + polygons[last_poly][1] + 
        polygons[last_poly][2]); // debug message

    // directly assign last polygons vertex's colors
    vertex_colors[get_index(polygons[last_poly][0])] = vertex_color.Red;
    vertex_colors[get_index(polygons[last_poly][1])] = vertex_color.Blue;
    vertex_colors[get_index(polygons[last_poly][2])] = vertex_color.Green;

    colorize(0); // start deep-first 3-color algorithm
}  

3-Coloring - colorize()

为顶点分配颜色的深度优先算法。

public void colorize(int i) // algorithm for colorizing points
{
    int next = i + 1;
    if (next < input_vertices.Length) // use deep-first strategy
    {
        colorize(next);
    }
    find_polygons(input_vertices[i]); // find given points related polygons
} 

3-Coloring - find_polygons()

查找与给定点相关的多边形。在3着色算法中使用，用于查找给定点相关的多边形，如果该找到的多边形中有未着色的顶点，代码会为其分配一个颜色。

public void find_polygons(Point p) // find given points related polygons
{
int v0_index, v1_index, v2_index;

    for (int i = polygons.Length - 1; i > -1; i--) 
                    // loop through all polygons
    {
        if ((p == polygons[i][0]) || (p == polygons[i][1]) || 
                 (p == polygons[i][2])) 
                // if given point is one of the vertexes of current polygon
                {
                    for (int j = 0; j < 3; j++) 
                        // check polygons all 3-vertexes colors
                    {           // vertexes are rounded and each one is 
                        // checked with two other
                        v0_index = get_index(polygons[i][j]);   // vertex1
                        v1_index = get_index(polygons[i][(j + 1) % 3]); 
                                                // vertex2
                        v2_index = get_index(polygons[i][(j + 2) % 3]); 
                                                // vertex3

                        if (vertex_colors[v0_index] == vertex_color.Empty) 
                            // if selected vertex's color is not set yet
                        {
                            vertex_colors[v0_index] = 
                            find_color(vertex_colors[v1_index], 
                                vertex_colors[v2_index]); 
                                // try to set a color to it using 
                                // other two vertexes colors
                                lb.Items.Add("[s" + v0_index + "] 
                            Assigned color: \t" + str_color
                            (vertex_colors[v0_index]) + " {" + 
                            str_color(vertex_colors[v1_index]) + 
                            " ," + str_color(vertex_colors[v2_index]) + 
                            "} " + polygons[i][j]); // debug message
                        }
                    }

                }
    }
}

运行程序

绘制多边形

使用鼠标左键标记多边形的顶点。
使用鼠标右键让程序完成多边形。

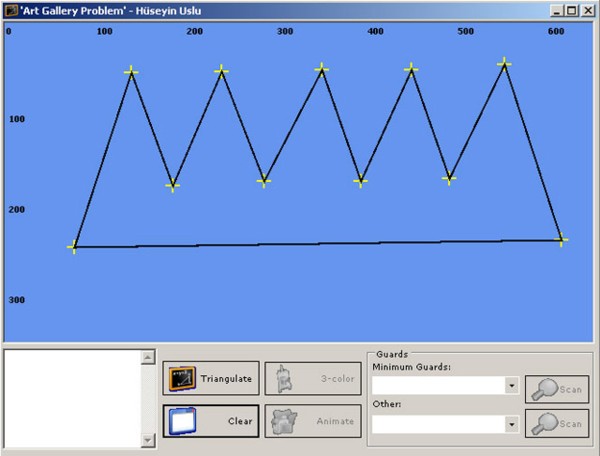
Triangulate

使用 Triangulate 按钮让程序运行三角剖分算法。

3-Color

使用 3-Color 按钮让程序对顶点进行 3 着色。

动画

程序可以通过 animate 按钮或单击 listbox 中的步骤来动画显示 3 着色算法。

Guard-Scanning

程序可以通过扫描按钮扫描选定警卫的视角区域。

历史

• 2007年5月4日 - 首次发布

参考文献

* 三角剖分代码主要基于 https://codeproject.org.cn/csharp/cspolygontriangulation.asp