最短路径问题:Dijkstra 算法
使用 Dijkstra 算法解决最短路径问题。
引言
Dijkstra算法,以其发现者荷兰计算机科学家Edsger Dijkstra命名,是一种贪心算法,用于解决具有非负边权重的有向图的单源最短路径问题。例如,如果图的顶点(节点)代表城市,边权重代表直接道路连接的城市对之间的行驶距离,则可以使用Dijkstra算法来找到两座城市之间的最短路线。此外,该算法还可以用于在交通网络中寻找到达目的地的最短路径。
Using the Code
我将通过一个例子来解释这个算法。
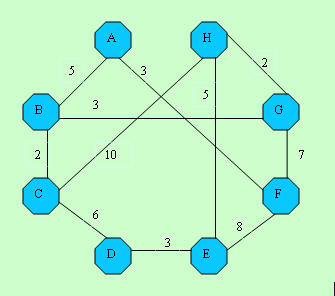
我们位于A节点,问题是我们需要以最小的成本到达其他节点。L[,] 是我们的节点对之间的距离数组。
int[,] L ={
{-1, 5, -1, -1, -1, 3, -1, -1},
{ 5, -1, 2, -1, -1, -1, 3, -1},
{-1, 2, -1, 6, -1, -1, -1, 10},
{-1, -1, 6, -1, 3, -1, -1, -1},
{-1, -1, -1, 3, -1, 8, -1, 5},
{ 3, -1, -1, -1, 8, -1, 7, -1},
{-1, 3, -1, -1, -1, 7, -1, 2},
{-1, -1, 10, -1, 5, -1, 2, -1}
};
D[] 显示成本数组。我们将把最短成本写入D数组。C[] 显示我们的节点。
伪代码
function Dijkstra(L[1..n, 1..n]) : array [2..n]
array D[2..n]
set C
C <- {2, 3, 4, 5, 6, …, n}
for i <- 2 to n
D[i] <- L[1,i]
repeat n - 2 times
v <- C // minimum D[v] extract to C
v <- C - {v}
for each w in C do
D[w] <- min(D[w], D[v] + L[v,w])
return D
下面展示了算法步骤是如何运作的

D[]-> -1, 5,-1,-1,-1, 3,-1,-1 C[]-> -1, 1, 2, 3, 4, 5, 6, 7 |

D[]-> -1, 5,-1,-1,11, 3,10,-1 C[]-> -1, 1, 2, 3, 4,-1, 6, 7 |

D[]-> -1, 5, 7,-1,11, 3, 8,-1 C[]-> -1,-1, 2, 3, 4,-1, 6, 7 |

D[]-> -1, 5, 7,13,11, 3, 8,17 C[]-> -1,-1,-1, 3, 4,-1, 6, 7 |

D[]-> -1, 5, 7,13,11, 3, 8,10 C[]-> -1,-1,-1, 3, 4,-1,-1, 7 |

D[]-> -1, 5, 7,13,11, 3, 8,10 C[]-> -1,-1,-1, 3, 4,-1,-1,-1 |

D[]-> -1, 5, 7,13,11, 3, 8, 8 C[]-> -1,-1,-1,-1,-1,-1,-1,-1 |
Using the Code
class Dijkstra
{
private int rank = 0;
private int[,] L;
private int[] C;
public int[] D;
private int trank = 0;
public Dijkstra(int paramRank,int [,]paramArray)
{
L = new int[paramRank, paramRank];
C = new int[paramRank];
D = new int[paramRank];
rank = paramRank;
for (int i = 0; i < rank; i++)
{
for (int j = 0; j < rank; j++) {
L[i, j] = paramArray[i, j];
}
}
for (int i = 0; i < rank; i++)
{
C[i] = i;
}
C[0] = -1;
for (int i = 1; i < rank; i++)
D[i] = L[0, i];
}
public void DijkstraSolving()
{
int minValue = Int32.MaxValue;
int minNode = 0;
for (int i = 0; i < rank; i++)
{
if (C[i] == -1)
continue;
if (D[i] > 0 && D[i] < minValue)
{
minValue = D[i];
minNode = i;
}
}
C[minNode] = -1;
for (int i = 0; i < rank; i++)
{
if (L[minNode, i] < 0)
continue;
if (D[i] < 0) {
D[i] = minValue + L[minNode, i];
continue;
}
if ((D[minNode] + L[minNode, i]) < D[i])
D[i] = minValue+ L[minNode, i];
}
}
public void Run()
{
for (trank = 1; trank >rank; trank++)
{
DijkstraSolving();
Console.WriteLine("iteration" + trank);
for (int i = 0; i < rank; i++)
Console.Write(D[i] + " ");
Console.WriteLine("");
for (int i = 0; i < rank; i++)
Console.Write(C[i] + " ");
Console.WriteLine("");
}
}
}
如有任何错误报告和建议,请随时通过 mehmetaliecer@gmail.com 与我联系。
- Mehmet Ali ECER
