策略游戏中的碰撞检测算法研究

摘要

碰撞检测算法的目的是检查物体是否相交。例如，在赛车游戏中，您想知道两辆车是否相撞以执行特定操作；或者在战略游戏中，您想在炸弹击中建筑物时采取行动，等等。

本文的目标是使用一种新算法，并通过使用和开发预定义的方程和算法来解决此问题。

关键词：战略游戏算法、物体边界、碰撞检测、物体相交、计算机图形学。

引言

在战略游戏中，开发人员使用平面作为游戏地面。在这个地面上，您会找到游戏对象。平面被划分为块；每个块都包含其中对象的处理器。如图 1 所示，平面被划分为一个块（实际上并未划分），因此开发人员必须在对象每次移动后，检查该块中的每个对象与其他所有对象是否重叠。

因此，如果同一个块中有两个对象，则需要一次检查迭代；但如果有三个对象，则需要检查三次；如果有 100 个对象，则需要检查 4950 次；这意味着算法运行 4950 次，依此类推。

C= <span style="FONT-FAMILY: Symbol; FONT-SIZE: 9pt">å</span>N from 1 to N-1

其中 C 是在特定块上运行算法的迭代次数，N 是此块上的对象数量。

请记住，每次增加块的数量，您都会增加这些块上的循环次数，并减少每个循环中的检查次数，因此您应该平衡大块和小块的大小。请记住，如果对象主体分布在多个块上，所有这些块都应该包含此对象的处理器。因此，这里关注的重点是只处理两个对象。算法返回一个逻辑值（布尔值）：如果两个对象相交则为 true，否则为 false。

对象边界

引言部分展示了影响算法的室外环境。在此步骤中，出现了一个新概念（对象边界）。每个对象都必须收集在一个数学形状中，以便在此形状上而不是在对象的网格上运行算法，因为如果我们直接在模型本身上工作，我们将处理大量表示该模型的方程。请记住，此处展示的算法是在战略游戏环境下进行的，因此在大多数情况下，算法的速度可能比算法的最佳和准确结果更重要。因此，请始终记住，我们希望在所需时间内解决 90% 的测试用例问题，而不是花费更多时间解决所有测试用例。还要记住，如果您有几十个对象，您可能需要在每帧运行此算法 100 次，每秒运行 2500 次，再加上该游戏中的其他算法。

如果如图 2 所示有两个对象，我们需要将这两个对象包含在几何形状中，以便能够在其上应用几何算法。现在出现两个选择，如下所示：

1. 如图 3 所示，第一个选项是将两个对象放入球体中。

   

   图 3. 球体中的对象
2. 将它们放入两个长方体中，如图 4 所示。

   

   图 4. 长方体中的对象

球体算法

如果我们使用圆形或球体，它比长方体更简单。每个对象都有 X、Y 和 R（其圆的半径）。

If (L < r1+r2)
Then
2 objects intersect themselves
Return true
Else
2 objects don’t intersect themselves
Return false

其中 L 是两个球体中心之间的距离，计算方法如下：

L <sup>2</sup>= (diffx<sup>2</sup>+diffy<sup>2</sup>+diffz<sup>2</sup>)

• 该算法的优点

  这是一种非常轻量级的算法，在运行时不会占用任何值。

• 该算法的缺点

  每个对象在此球体中都占据了很大的自由空间。图 3 中的两个对象将被视为相交对象，尽管它们彼此相距很远。

长方体算法

在图 4 中，长方体形状被用作对象容器。它比球体更精确（但也更复杂）。因为我们正在处理在同一平面上运行的对象之间的碰撞检测，所以我们将忽略顶部的 4 个点——假设你我不会相交，如果我们的脚不相交。所以我们将专注于矩形算法而不是长方体。这里，图 6 展示了两个不相交的对象的例子。

因此，如果我们分析这些矩形，我们会发现任何矩形都是由点和线组成的，我们将把我们的想法分为：

• 点算法
• 线算法

点算法

这个想法假设当其中一个或多个点位于另一个对象的边界之间时，矩形会相交。

点算法 1 (中点边界)

在这个算法中，两个对象被称为 A 和 B。第一步是遍历对象 A 的点。循环中的临时值称为 temp，其坐标为 temp_x 和 temp_y，我们用对象 B 的边界来检查它们。

Loop on object “A” points, set temp to variable in loop
{
If (
B_object_x_minimum<= temp_x
And     B_object_x_maximum>= temp_x
And     B_object_y_minimum<= temp_y 
And    B_object_y_maximum>= temp_y 
)
Then 
    This point from A is in boundaries of B, return true, leave algorithm
Else
                This point from A is not in boundaries of B
 }
Get one point from object “B” points, set temp to this point
If (
A_object_x_minimum<= temp_x
And     A_object_x_maximum>= temp_x
And     A_object_y_minimum<= temp_y 
And    A_object_y_maximum>= temp_y 
)
Then 
          This point from B is in boundaries of A, return true, leave algorithm.
When reach this step so no intersection between two objects, return false.

但是，如果矩形 B 不稳定（没有与 X 轴平行或与 Y 轴平行的线），我们就无法处理最小和最大的 X、Y 值。为了解决这个问题，您可以将两个矩形旋转一个角度，使不稳定的对象 B 变得稳定。

注意：但如果您追溯此算法，您会发现，如果 A 中没有点位于 B 的边界内，并且仅检查“B”对象的一个点，则您已经逻辑上完成了算法，无需检查 B 的其他三个点。这将使您在最坏情况下只检查五个点，而不是八个点。因此，通过注意此说明，您将减少算法复杂性 3/8 (37.5%)。

复杂性降低提示

首先，在此算法中，您应该检查两个矩形中是否有一个是稳定的，以便在第一个循环中依赖它（将其视为 B）——这样就省去了旋转的麻烦，特别是如果第一个循环可能会返回您正在寻找的答案——即两个对象相交。然后根据另一个矩形，如果它不稳定，您将旋转它，并且只使用对象 B 中的一个点，您不必为对象 B 中的其他三个点制作旋转方程。

Search for stable rectangle
If find
{
Make object b= this stable rectangle.
Object a= another rectangle.
}
Else
{
Rotate 2 rectangles (8 points) by the angle of any rectangle line slop.
This rectangle which you get slop from it become stable now so b=this rectangle.
Object a= another rectangle.
}
For each point of A
{
If (this point in boundaries of B)
Then
There are intersection between A and B
Leave algorithm
}
 
if object (a) is not stable
{
Rotate object (a) by the angle of any its’ lines slop.
Rotate one point from object (b) with the same slop.
}
Check only this rotated point of object “B”
{
If (this point in boundaries of A)
Then
There are intersection between A and B
Leave algorithm
}
If come for here so there are no intersection between A and B
Note the rotation formulas of any point by angle are:
X = x * cos (q) – y * sin (q)
Y = x * sin (q) + y * cos (q)

其中 X 和 Y 是 x 和 y 的新值。

点算法 2（边界上的点面）

此算法依赖于点及其在线上的面。如果点在矩形边界之间，则其在矩形线上的四个面都在线上，如图 7 所示。

但如果点在矩形之外，则它有一面或多面在线上，而不是在线本身上，如图 8 所示（实心蓝线表示从点及其面引出的线，虚线绿线表示矩形线的延伸，黑色矩形表示对象的矩形）。

数学上解决这个想法

从图 9 中，我们发现点与其面之间的线与水平线之间的夹角，等于底线与垂直线之间的夹角。因此，通过分析包含这两个角度的两个三角形，如图 10 (EDF) 和 (BAC) 所示，我们可以发现

A is the point 
C is the face of point A on DE
CG is vertical line
DE is the line that we worked on
B is the point with the same y value as “A” and on the line DE
F is the point with “D” x value and “E” y value
^(BCG)=^(EDF)
^(BCG)+^(CBG)=90 && ^(CAG)+^(CBG)=90
So
^(BCG)=^(CAG)=^(EDF)
^(ACB)=^(DFE)=90
^(ABC)=^(DEF)
While 3 angles in 2 triangles equal themselves, so 2 triangles are similar.
So
Line (AB)/line (DE)=line (AC)/line (DF)                  (1)
 
While point (B) is on the line (DE), the equation of line (DE) is
Y=ax+b
Y is a the same y of point “A”
A is slope of line DE=(D.y-E.y) / (D.x-E.x)
B is Y-axis displacement of line (DE)
So I can get x of point “b”
So
Line (AB) known length
Line (DE) known length
Line (DF) known length
So I can get length of line (ac) and set in “value” variable
(A.y-C.y)2+(A.x-C.x)2=value2
Where C.y=(a*C.x)+b   (line equation)
“a” and “b” can known from line(DE)
(A.y- ((a*C.x)+b))2+(A.x-C.x)2=value2
This equation has only one unknown variable (C.x)
So we can get C.x value and from line (DE) or (AC) equation we can get C.y value.
After getting x and y of point “C” we can say if “C” on the line (DE) or not.

当然，该算法的实现并不包含所有这些方程；您只需放入给出所需值的方程。

在遍历一个对象的四个点之后，您必须只检查另一个对象的一个点——如上面边界算法中的点。检查另一个对象的一个点是为了处理图 11 中的特殊情况。如果您依赖黑色对象，您将发现灰色对象中没有点在黑色矩形中，尽管这两个对象是相交的。

这两种算法都无法涵盖所有情况，因为存在如图 12 所示的特殊情况，点算法无法涵盖，因为这两个对象相交，尽管每个对象都没有点在另一个对象的体内。

线算法

这类算法的基本思想集中在线的交点，而不是点存在于另一个对象的体内。

线算法 1（碰撞检测堆算法）

这是基于以下规则：如果两个矩形中没有一个点在另一个矩形体内，并且这两个矩形的两条线之间没有交点，则它们不相交。

让我们看看最后一个算法，它将通过考虑点和线的交点来解决问题。通过开发另一种现有算法，即线裁剪中的 Cohen Sutherland 算法 [2]，并将其用于我们的目的。我们创建了一种新的内存位置形式——块——用于保存变量。这种形式有四个位置：LEFT、RIGHT、UP 和 DOWN。

这个数据结构根据每个点相对于另一个矩形的位置分配给两个矩形中的每个点。如果该点在另一个矩形的左侧，则应将其左侧位置设为 1，否则设为 0，依此类推。

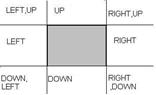
在图 14 中，灰色矩形是 2 个矩形中的一个——稳定的矩形。完成这 4 个位置后，如果点在另一个矩形中，所有四个变量都将为 0。通过进行位或运算，如表 1 所示，结果=0，这意味着这两个对象相交。

A 左	0
A 右	0
A 上	0
A 下	0
总计	0

这里我们将在线上操作。如果存在两个点之间包含一条线，并且这两个点拥有两个相反的变量 =1，那么这条线将与矩形相交，如图 15 所示。

通过进行位与操作，如表 2 所示，结果=1，因此这两个对象相交。

B 左	1
A 右	1
总计	1

如果两个点具有相同的变量 =1，则它们之间的线不与矩形相交——因为这两个点都在矩形的左侧。

该算法的复杂部分是，如果我们没有找到这些情况中的任何一种，我们必须对该行进行更多的分析，因为仅这四个变量无法给我们决策——是否存在交叉。例如，以下两行具有不同的决策，尽管它们的点具有相同的值，如图 16 和图 17 所示。

在这里，我们将对两个点值进行一个小的计算，以得出我们的决定。我们将对两个点变量进行位或计算，如表 2 所示。

	左	右	上	下
A	0	0	1	0
B	0	1	0	0
总计	0	1	1	0

从结果中，我们得到必须检查 A、B 之间的线与矩形中右侧和上方的线，这会从 OR 运算中产生 1。

通过使用直线方程，我们可以得到两条直线之间的交点，因此如果这个点在矩形线上，则存在交点；如果它在其延伸线上，则没有交点。

Calculate A point’s variable
Loop on points
{
    If (the point in another object)  -OR between 4 variables-
    Then 
    Intersected objects, Leave algorithm
}
Loop on lines
{
    If (line points in same location)
    Then 
    Go to another line and repeat the loop
    If (line points in inverse location)
    Then 
    Intersected objects, Leave algorithm
    Else
    {
       Calculate which lines expected that might intersect (as table 3) 
       Loop on these lines
       {
            Calculate the intersection point by line equation
            If (intersected point on the boundary line itself)
            Then
            Intersected objects, Leave algorithm
            Else
            Go to another line and repeat the loop
       }
    }
}
Calculate one of B point variable
If (the point in object “A”)
Then 
Intersected objects, Leave algorithm
If come for here so there are no intersection between A and B

算法的最后一部分（计算 B 的一个点…）是为了处理图 11 中的情况，如果您将黑色矩形作为“B”对象。

参考文献

• [1] Bruno Miguel teixeira de sousa “Game Programming All In One”，游戏开发系列，Premier Press。
• [2] Donald Hearn 和 M. Pauline Baker “计算机图形学 C 版” 第二版。Prentice Hall。

历史

• 版本 1：2011 年 6 月 5 日，初始版本。