使用小波变换进行图像边缘检测

• 下载演示项目 - 38.8 KB
• 下载源代码 - 47.3 KB

引言

边缘检测用于计算机视觉应用中，提取物体的轮廓。常用的方法是使用图像与复杂的滤波器（如Sobel或Prewitt）进行卷积运算。

Sobel 滤波器

Real
1.0  0.0 -1.0
2.0  0.0 -2.0
1.0  0.0 -1.0
Imaginary
1.0  2.0  1.0
0.0  0.0  0.0
-1.0 -2.0 -1.0

Prewitt 滤波器

Real
0.5  0.0 -0.5
0.5  0.0 -0.5
0.5  0.0 -0.5
Imaginary
0.5  0.5  0.5
0.0  0.0  0.0
-0.5 -0.5 -0.5

例如，您可以使用我在文章 Vector Class Wrapper SSE Optimized for Math Operations 中描述的 vec2D 包装器来提取边缘。

然而，除非进行整数优化，否则浮点运算可能需要很长时间。 使用小波变换，您可以使用一些数学运算获得类似的结果。 例如，图像的Haar变换提供了该图像的细节，这些细节包含在高频带中，如果您在同一图像上使用X和Y差分滤波器，则外观非常相似。

X 差分滤波器

0.0  0.0  0.0
0.5  0.0 -0.5
0.0  0.0  0.0

Y 差分滤波器

0.0  0.5  0.0
0.0  0.0  0.0
0.0 -0.5  0.0

如果我们保留使用Haar变换获得的图像细节，移除粗粒度的低频分量并执行图像重建，我们将获得图像中存在的物体的边缘。

背景

需要 边缘检测 的图像处理背景知识。 您也可以参考我关于图像数据小波分析的文章： 用于图像处理的2D快速小波变换库 和 使用Haar变换的快速二元图像缩放。

Using the Code

代码和演示应用程序来自我的文章 用于图像处理的2D快速小波变换库，您可以在其中找到有关如何运行代码和使用库的详细信息。 在此项目中，我添加了几个边缘特定的操作，因此您可以尝试使用不同的小波滤波器、尺度和去噪阈值来选择最佳组合。 下面我演示了daub1 滤波器的应用，它是Haar变换中使用的滤波器。

打开图像并将其转换为 1、2 或 3 个尺度。 您可以添加阈值来消除噪声。 下面，选择 daub1 滤波器进行 1 尺度变换，不进行去噪

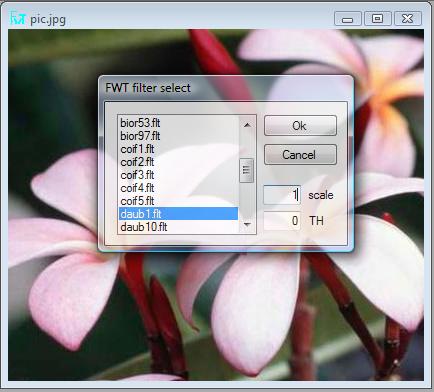
您将获得此 FWT 频谱

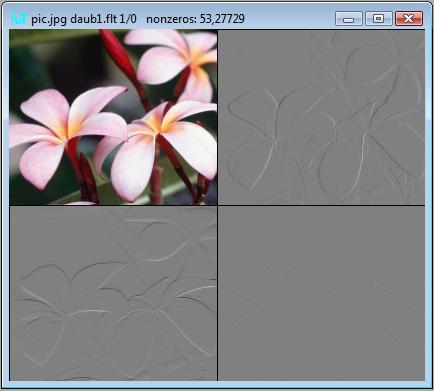
现在单击转换->去噪菜单项以移除低频分量

您可以在 BaseFWT2D 类中找到相应的函数

void BaseFWT2D::remove_LLband()
{
        if (m_status <= 0)
                return;

        unsigned int width = m_width / 
            (unsigned int)(pow(2.0f, (float)getJ()));
        unsigned int height = m_height / 
            (unsigned int)(pow(2.0f, (float)getJ()));
        
        for (unsigned int y = 0; y < height; y++) 
                for (unsigned int x = 0; x < width; x++)                     
                        spec2d[y][x] = 0;                
}

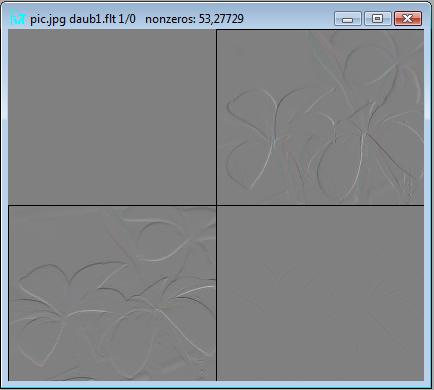
现在您可以重建图像

看起来还不像边缘。您只需要从图像中减去128，然后使用变换->绝对值菜单项计算绝对值

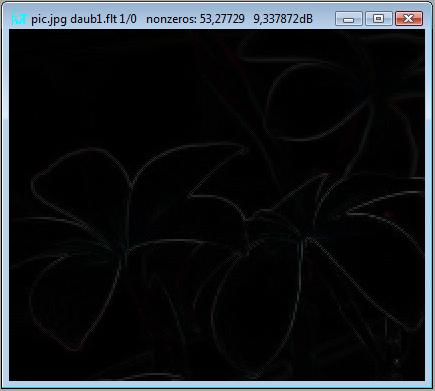
但是边缘相当模糊。 首先，我进行了对比度拉伸，即将图像归一化到0 ... 255范围。 但是可能在范围的上限处有几个像素，并且它并没有真正改善这种情况。 更好的选择是非线性归一化，例如对数刻度，但我只是将像素数据乘以某个值，并获得更突出的边缘。 对于 1 尺度变换，乘以 7 效果很好，并且对于大多数像素而言，不会溢出 255 限制，但是对于 2 或 3 个尺度，您可能会减小乘法数。

现在单击变换->对比度拉伸以放大您的边缘

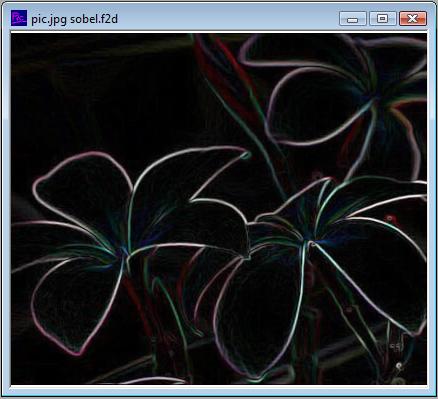
您可以比较我使用Sobel滤波器获得的相同图片结果。它看起来更平滑，但是您可以继续进行诸如腐蚀和膨胀之类的形态学操作，并获得轮廓的细骨架，因此最终，结果将非常接近。

我已经开发了Haar变换MMX优化，并且将来计划将代码更新为EdgeDetector类或类似的东西，并比较性能。