计算机视觉应用中的线性秩亏损滤波器

• 下载演示 - 64.5 KB
• 下载源代码 - 11.1 KB

引言

在计算机视觉中，您经常需要使用某个滤波器执行图像卷积运算。例如，图像增强、边缘检测、高斯平滑，或使用 PCA、LDA、ICA、MP 或任何其他一组向量表示的低维空间投影来检测对象。处理更大尺寸的图像会增加运算时间。最近，我发现了一篇很棒的文章，Face Detection - Efficient and Rank Deficient，其中作者将一种方法应用于支持向量机（SVM）分类器的秩亏损近似。通过秩亏损近似，普通的卷积需要O(w*h)次滤波运算，而该方法可以将运算速度提高到仅需O(w+h)次运算，其中w和h是图像的大小。因此，我决定为我自己的计算机视觉项目编写代码实现该方法，并观察其性能。

背景

在本文中，vec2D 类是从我之前的文章《SSE 优化的 2D 向量类包装器，用于数学运算》中扩展而来的。如果您不熟悉卷积运算，可以参考 Wiki。

算法

给定一个线性滤波器H并将其应用于图像I，会得到一个二维卷积运算

J = I * H;

因此，J的大小与I相同。

如果H的大小为h x w，则每次输出像素的卷积需要O(h*w)次运算。然而，在特殊情况下，如果H可以分解为两个列向量a和b，使得

H = ab';

则卷积运算变为

J = [I * a] * b';

由于卷积是可结合的，并且在这种情况下，ab' = a * b'。这将原始的卷积运算分解为两次运算，分别使用大小为h x 1和1 x w的向量。结果是，如果一个线性滤波器是可分离的(H = ab')，那么每个像素的滤波运算的计算复杂度将从O(h*w)降低到O(h + w)。

奇异值分解（SVD）用于将H滤波器分解为a和b向量。

H = USV';

U和V分别是大小为h x h和w x w的正交矩阵。S是一个对角矩阵（对角线上的元素是奇异值），大小为h x w。设r = rank(H)。由于rank(S) = rank(H)，我们可以将H写成r个秩一矩阵的和。

(1)

其中，s表示H的第i个奇异值，而u和v分别是U和V的第i列（即矩阵H的第i个奇异向量）。结果是，相应的线性滤波器可以评估为r个可分离卷积的加权和

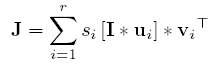(2)

并且每个输出像素的计算复杂度从O(h * w)降低到O(r * (h + w))。速度提升的幅度取决于r，r可以看作是衡量H的结构复杂度的指标。

您可以选择r，直到（1）式中H滤波器的重构误差低于某个阈值。显然，滤波器越复杂（即包含越高频成分），所需的r就越大，但像高斯滤波器这样简单的滤波器可以用r = 1近似得非常好。

下面展示了一个特征脸（Eigen face）

以及其在 1、2 和 3 次迭代（即r = 1, 2, and 3）后的重构结果

可以看出，随着r的增加，均方误差（MSE）减小。

使用代码

下面分别展示了一个普通卷积和一个秩亏损卷积

//this = a * filter;
void vec2D::conv2(const vec2D& a, const vec2D& filter, 
                  enum CONV type)  //filter should be of odd size
{
    int l = filter.height() / 2;
    int m = filter.width() / 2;        

    vec2D& c = *this;

    if (type == SAME) {      //this size = a size        
        for (int i = 0; i < (int)c.height(); i++) {
            for (int j = 0; j < (int)c.width(); j++) {
                float tmp = 0;                        
                for (int u = i - l; u <= i + l; u++)
                    for (int v = j - m; v <= j + m; v++) 
                        tmp += filter((i-u)+l, (j-v)+m) * a.get(u, v);
                c(i, j) = tmp;
            }
        }
    }
    else if (type == VALID) { //this size = (a size - filter size) + 1        
        for (int i = l; i < (int)a.height() - l; i++) {
            for (int j = m; j < (int)a.width() - m; j++) {
                float tmp = 0;                        
                for (int u = i - l; u <= i + l; u++)
                    for (int v = j - m; v <= j + m; v++) 
                        tmp += filter((i-u)+l, (j-v)+m) * a(u, v);
                c(i - l, j - m) = tmp;
            }
        }
    }
}

使用enum vec2D::CONV，您可以选择类似 Matlab 的风格来执行卷积，此时输出数组与卷积数组大小相同，或者只卷积滤波器能够完全适应的图像区域，而不进行零填充。

//this = sum( s[i] [a * u[i]] * v[i])
void vec2D::conv2(const vec2D& a, const std::vector<vec2D>& u,  //col vectors
                  const std::vector<vec2D>& v,  //row vectors
                  const vec2D& s,   //row vector singular values
                  vec2D& tmp1,  //tmp1 = [(a.height - u.height + 1) x a.width]
                  vec2D& tmp2,  //tmp2 = this = [(a.height - u.height + 1)
                                    //                x a.width - v.width + 1]
                  enum CONV type)
{                                   
    vec2D& c = *this;
    c.set(0.0);
    for (unsigned int i = 0; i < s.width(); i++) {
        tmp1.conv2(a, u[i], type);
        tmp2.conv2(tmp1, v[i], type);
        tmp2.mul(s(0, i));
        c.add(c, tmp2);
    }
}

对于秩亏损函数，您需要提供std::vector数组中的u和v向量，s是奇异值的行向量，而tmp1和tmp2是临时缓冲区。对于VALID卷积，我注释掉了它们的尺寸。

如果您要将图像投影到某个 PCA、LDA、ICA 或类似的基上，请记住在执行 SVD 之前旋转您的滤波器，或者在计算卷积之前旋转u、v向量。

void vec2D::fliplr()
{
    vec2D& c = *this;
    float tmp;

    for (unsigned int i = 0; i < width() / 2; i++) {
        for (int y = yfirst(); y <= ylast(); y++) {
            tmp = c(y, xfirst() + i);
            c(y, xfirst() + i) = c(y, xlast() - i);
            c(y, xlast() - i) = tmp;
        }
    }
}
void vec2D::flipud()
{
    vec2D& c = *this;
    float tmp;

    for (unsigned int i = 0; i < height() / 2; i++) {
        for (int x = xfirst(); x <= xlast(); x++) {
            tmp = c(yfirst() + i, x);
            c(yfirst() + i, x) = c(ylast() - i, x);
            c(ylast() - i, x) = tmp;
        }
    }
}
void vec2D::rotate180()
{
    vec2D& c = *this;
    c.fliplr();
    c.flipud();
}

结果

下面展示了一个 192x256 数组与一个 19x19 滤波器的卷积结果。首先是与特征脸卷积的原始图像

下面展示了r = 1, 2, 3的秩亏损卷积以及该图像的普通卷积

可以看出，随着r的增加，普通卷积结果与秩亏损卷积结果之间的均方误差（MSE）减小。

并且，卷积的计时结果如下

SAME
 J = I * H    processing time: 142.258583 ms

 J = sum (s[i] [I * u[i]] * v[i]'); i < 1    processing time: 20.521044 ms
 J = sum (s[i] [I * u[i]] * v[i]'); i < 2    processing time: 42.043612 ms
 J = sum (s[i] [I * u[i]] * v[i]'); i < 3    processing time: 63.772351 ms

VALID
 J = I * H    processing time: 88.931973 ms

 J = sum (s[i] [I * u[i]] * v[i]'); i < 1    processing time: 14.583697 ms
 J = sum (s[i] [I * u[i]] * v[i]'); i < 2    processing time: 28.884118 ms
 J = sum (s[i] [I * u[i]] * v[i]'); i < 3    processing time: 42.637542 ms

对于线性秩亏损滤波器卷积，结果分别展示了 1、2 和 3 次迭代的情况。

SAME 模式会生成与I大小相同的 J 数组，适用于图像滤波（例如，高斯平滑、边缘检测、图像增强）。VALID 模式是滤波器完全适应 J 数组而无需零填充的卷积，因此 J 数组会比原始 I 数组小。后者适用于将图像投影到某个基上（例如，PCA、LDA、ICA、MP、Gabor 滤波器等），当您需要分析图像中滤波器完全适应的区域（例如，在计算机视觉任务中检测人脸、汽车或其他对象）而无需零填充时。