近似熵和样本熵复杂度度量

引言

有无数信号可以使用谱分析方法进行分析：医学（HRV、ECG、EEG、EMG）、地质、音乐等。在不同的分析方法中，有一组旨在估计信号复杂度的复杂度指标。考虑正弦波和随机噪声。显然，正弦波是一种简单的信号形式，而噪声则更复杂。近似熵（ApEn）和样本熵（SmEn）指标可以提供这种信号复杂度程度的定量估计。ApEn 和 SmEn 更适合于短期噪声信号的复杂度估计。它们具有优势，即它们分析原始信号，因为一些复杂度指标需要将原始信号量化为非常小的字母表。因此，它们在医学上广泛用于 HRV 数据分析。对于 EEG 数据分析，它们可用于估计一些复杂的神经元活动。

背景

您应该阅读我的 文章，关于应用 ApEn 和 SmEn 分析 HRV 数据以预测阵发性心房颤动。在那里，提供了更详细的解释。这里只是 ApEn 和 SmEn 的公式。

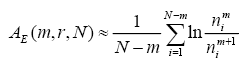
Using the Code

ApEn 代码如下所示

double ApEn(const double* data, unsigned int m, double r, unsigned int N, double std)
{
        int Cm = 0, Cm1 = 0;
        double err = 0.0, sum = 0.0;

        err = std * r;

        for (unsigned int i = 0; i < N - (m + 1) + 1; i++) {
                Cm = Cm1 = 0;
                for (unsigned int j = 0; j < N - (m + 1) + 1; j++) {
                        bool eq = true;
                        //m - length series
                        for (unsigned int k = 0; k < m; k++) {
                                if (abs(data[i+k] - data[j+k]) > err) {
                                        eq = false;
                                        break;
                                }
                        }
                        if (eq) Cm++;

                        //m+1 - length series
                        int k = m;
                        if (eq && abs(data[i+k] - data[j+k]) <= err)
                                Cm1++;
                }

                if (Cm > 0 && Cm1 > 0)
                        sum += log((double)Cm / (double)Cm1);                
        }

        return sum / (double)(N - m);
}

SmEn 代码接下来展示

double SmEn(const double* data, unsigned int m, double r, unsigned int N, double std)
{
        int Cm = 0, Cm1 = 0;
        double err = 0.0, sum = 0.0;

        err = std * r;

        for (unsigned int i = 0; i < N - (m + 1) + 1; i++) {
                for (unsigned int j = i + 1; j < N - (m + 1) + 1; j++) {      
                        bool eq = true;
                        //m - length series
                        for (unsigned int k = 0; k < m; k++) {
                                if (abs(data[i+k] - data[j+k]) > err) {
                                        eq = false;
                                        break;
                                }
                        }
                        if (eq) Cm++;

                        //m+1 - length series
                        int k = m;
                        if (eq && abs(data[i+k] - data[j+k]) <= err)
                                Cm1++;
                }
        }

        if (Cm > 0 && Cm1 > 0)
                return log((double)Cm / (double)Cm1);
        else
                return 0.0; 

}

N 是 data 指向的信号的大小，std 是信号的离散程度，r 通常用作 0.2。SmEn 和 ApEn 衡量的是长度为 m 时与长度为 m+1 时有多少相似模式（在误差 r * std 内）。

历史

• 2008 年 6 月 17 日：初始发布