求解线性和多项式方程

• 下载演示 - 33.11 KB
• 下载源代码 - 1.47 KB

引言

线性和多项式方程应用于许多不同的领域。因此，求解这些方程对许多人来说都很有用。此应用程序具有求解线性和多项式方程的方法。用户可以选择多项式或线性方程，然后给出相关参数。有一个GUI表单可以输入参数，以便用户更容易理解。

背景

线性方程

以下格式的方程被称为线性方程

51x+4y+38z = 35

在上述方程中，x、y 和 z 是未知数。如果想要求解 3 个未知数，则需要 3 个包含这些未知数的方程。

多项式方程

以下格式的方程被称为多项式方程

4x^3+7x^2-12=0

多项式方程只有一个未知变量。在上述方程中，x 是未知变量。未知变量的最高次幂称为方程的阶数。上述方程的阶数为 3。多项式方程的最大解数是该方程的阶数。

求解方程

未知数的个数应等于方程的个数，才能获得线性方程的解。矩阵行运算用于求解线性方程。牛顿-拉夫森方法用于求解多项式方程。

该程序有三个 GUI 表单，用于从用户那里获取输入。第一个表单用于获取方程的类型和方程的参数数量。换句话说，未知数的个数或方程的阶数。

求解线性方程

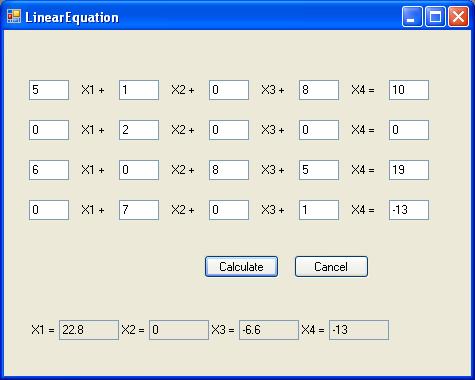
上面的表单用于获取求解线性方程的输入。用相关值填写表格。未知数被标记为 X1、X2 等。然后单击“计算”按钮。

求解多项式方程

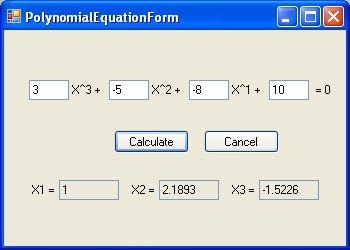
上面的表单用于获取用户的输入。下面的文本框在单击“计算”按钮后给出输出值。

Using the Code

求解线性方程

假设您需要求解以下 3 个方程

• 4x+23y-6z = 3
• -7x+3y+12z = 25
• 5+10y-7z = 30

它可以写成如下的矩阵乘积形式

[4 23 -6] [x] .. [ 3]
[-7 3 12] [y] = [25]
[5 10 -7] [z] .. [30]

有 3 个矩阵

1. 系数矩阵 (3,3)
2. 未知变量矩阵 (3,1)
3. 答案矩阵 (3,1)

假设未知数的个数为 'n'。然后考虑第一个矩阵 (n,n) 和第三个矩阵 (n,1)，合并这两个矩阵并创建一个二维数组 (n,n+1)。

示例（对于上述方程）

[4 23 -6 | 3]
[-7 3 12 |25]
[5 10 -7 |30]

然后通过行运算将系数矩阵制成单位矩阵。矩阵乘法不会因为行运算而改变。因此，答案矩阵变成了未知数的解。

for (int i = 0; i < nVar; i++)
{
    //If the element is zero, make it non zero by row operation
    if (equationMatrix[i, i] == 0)
    {
        int j;
        for (j = i+1; j < nVar; j++)
        {
            if (equationMatrix[j, i] != 0)
            {
                for (int k = i; k < nVar + 1; k++)
                    equationMatrix[i, k] += equationMatrix[j, k];
                break;
            }
        }
        //If all value for this variable is zero, there should a duplicated equation
        if (j == nVar)
            throw new Exception("Same equation repeated. Can't solve it");
    }

    //make the diagonal element as 1
    for (int k = nVar; k >= i; k--)
        equationMatrix[i, k] /= equationMatrix[i, i];

    //use row operation to make upper matrix
    for (int j = i+1; j < nVar; j++)
    {
        for (int k = nVar; k >= i; k--)
            equationMatrix[j, k] -= equationMatrix[i, k]*equationMatrix[j,i];
    }
}

//It is to make diagonal matrix
for (int i = nVar-1; i > 0; i--)
{
    for(int j=i-1; j>=0; j--)
    {
        equationMatrix[j, nVar] -= equationMatrix[j, i] * equationMatrix[i, nVar];
        equationMatrix[j, i] = 0;
    }
}

double []ans = new double[nVar];
for(int j=0; j < nVar; j++)
    ans[j] = equationMatrix[j,nVar];

求解多项式方程

它使用牛顿-拉夫森方法。这是一种近似方法。因此，需要更多的迭代才能获得更准确的值。此程序的精度约为 0.0001。迭代次数根据答案的精度而变化。

while (Math.Abs(x - x0) > 0.0001)
{
    if (itr++ > maxIteration)
    {
        return NoSolution;
    }
    x0 = x;
    func = 0; dFunc = 0;
    for (int i = 0; i < coefficient.Count; i++)
    {
        func += coefficient[i] * Math.Pow(x, coefficient.Count-1 - i);
    }
    for (int i = 0; i < dCoeff.Count; i++)
        dFunc += dCoeff[i] * Math.Pow(x, dCoeff.Count-1 - i);

    if (dFunc != 0)
        x = x - func / dFunc;
    else if (func < 0.0001)
        return x;
    else
        x += 1;
}

注意

方法 "List<double> SolvePolynomialEquation(List<double> coeffient)" 和 "double[] SolveLinearEquation(double[,] equationMatrix)" 能够求解阶数大于 10 的方程。我在本程序中将方程的阶数限制为 10。

关注点

有一个初始值，然后使用近似方法来获得多项式方程的解。如果您知道方程的近似值，则给出该值以减少迭代次数。

历史

• 2011 年 11 月 2 日：初始版本