Alphablend 代码的 SSE2 向量化
4.97/5 (19投票s)
使用 SSE2 加速 alpha 混合。
目录
引言
在本文中,我们将探讨如何对我在上一篇文章中编写的像素 alpha 混合代码进行向量化。我相信大多数 C/C++ 程序员都曾尝试过 SIMD 指令,如 MMX 和流式 SIMD 扩展 2 (SSE),甚至高级向量扩展 (AVX)。但大多数程序员,我想,在第一次 SIMD 尝试失败后就放弃了,因为他们的努力所产生的性能比原始的非向量化代码要差,甚至更差。性能缓慢的主要原因在于,CPU 时钟周期通常浪费在将基本数据打包到向量中以进行 SIMD 执行,以及在执行后将它们解包回结构中的正确位置。我们将在下一节深入探讨这一点。SIMD 之所以难以被全球程序员普遍采用,主要原因在于 SIMD 代码更难编写,即使使用了内在函数,生成的代码也不易读,更难理解。
在本文中,我们将只关注 SSE2;原因是 MMX 是一种 64 位 SIMD 技术,与 SSE2(英特尔提供的主要是 128 位 SIMD)相比,在当今的 64 位处理器上速度提升不明显。而高级向量扩展 (AVX)(英特尔提供的 256 位 SIMD)之所以没有被选择,是因为并非许多主流用户拥有可以利用 AVX 的最新英特尔处理器:SSE2 自 2001 年以来就已存在。(好吧,我承认,真正的原因是我没有 AVX 支持的处理器。我承诺在我能够访问一台带有 AVX 兼容处理器的 PC 时更新这篇文章。)所有除最老的个人电脑外,都应该配备支持 SSE2 的 x86/x64 处理器。我们将使用 Visual Studio 提供的 SSE2 内在函数来调用 SSE2 指令,而不是使用内联汇编代码:目前,微软的 64 位 C/C++ 编译器不允许内联汇编代码。
数组结构
让我们想象一下,我们有一个名为 SomeStruct 的结构类型,如下所示,并且我们有一个 SomeStruct 的数组,本质上就是一个结构数组。
struct SomeStruct
{
int aInteger;
double aDouble;
short aShort;
};
要对 aInteger 使用 SSE2 算术指令,我们必须首先将四个 aInteger 打包到一个 128 位整数类型向量 __m128i 中。

在我们获得计算结果后,我们必须将这四个 aInteger 解包到数组中的各个结构对象中。

这通常是拖慢性能的罪魁祸首!为了提高性能,建议程序员将数据打包到数组结构(structure of arrays)而不是结构数组(array of structures)中;同样的建议也适用于 GPGPU 编程,以便实现内存合并。改变现有的数据域/模型以不自然地适应 SIMD 数据打包要求,通常是不可能的。在下面所示的结构中,arrInteger、arrDouble 和 arrShort 通常是指向动态分配数组的指针,其大小仅在运行时可知,但我在此处将它们显示为数组类型,以强调它们是数组类型而不是指针类型。
struct SomeStruct
{
int arrInteger[1000];
double arrDouble[1000];
short arrShort[1000];
};
正如读者可能已经注意到的,整数、双精度浮点数和短整数数据类型有不同的字节大小。四个整数可以放入 __m128i,两个双精度浮点数可以放入 __m128i,而八个短整数可以放入 __m128i。这在程序员编写代码循环遍历 __m128i 数组进行计算时可能会遇到困难。对我们来说,这不是问题,因为在这个 alpha 混合文章中,我们只使用 unsigned short 类型。

代码解释
对于我们的 SSE2 alpha 混合代码,正如我刚才所说,我们将使用 unsigned short 类型来存储每个颜色通道。读者可能会问,为什么使用 unsigned short 来存储一个仅范围在 0 到 255 的值?答案是因为在乘法运算中,中间值很可能超过 255,而最终结果仍会保持在 255 以内。在普通编码中,我们可以使用字节变量进行相同的计算,而不使用 16 位变量。原因是字节值在进行任何计算之前会自动提升为整数(平台的本机字长),并在计算后自动转换回字节。我们声明了一个 __m128i 数组来存储两个 alpha 混合图像每个颜色通道的 unsigned short。m_fullsize 用于存储数组的完整大小(以字节为单位)。m_arraysize 是以 128 位大小元素为单位的数组大小。m_remainder 用于存储一个数字,该数字指示在最后一个 128 位元素中有多少个 unsigned short 是有效的,如果所需的 unsigned short 的数量不能被 8 整除(8 x 16 位 = 128 位)。例如,四个整数可以放入 __m128i;如果我们有六个整数需要计算,则需要一个包含两个 __m128i 元素的数组,但在最后一个 __m128i 元素中,仅使用了两个整数,因此 m_remainder 将反映 2。
__m128i* m_pSrc1R;
__m128i* m_pSrc1G;
__m128i* m_pSrc1B;
__m128i* m_pSrc2R;
__m128i* m_pSrc2G;
__m128i* m_pSrc2B;
// the full size of array in bytes
int m_fullsize;
// the full size of array in 128-bit chunks
int m_arraysize;
// the remainder of last 128-bit element
// which should be filled.
int m_remainder;
通过 GetUShortElement 方法,我们可以使用一个以 unsigned short 元素为单位的索引,从 __m128i 数组中获取一个 unsigned short 元素。
unsigned short& CAlphablendDlg::GetUShortElement(
__m128i* ptr,
int index)
{
int bigIndex = index>>3;
int smallIndex = index - (bigIndex<<3);
return ptr[bigIndex].m128i_u16[smallIndex];
}
通过 Get128BitElement 方法,我们可以使用一个以 __m128i 元素为单位的 bigIndex,从 __m128i 数组中获取一个 __m128i 元素。bigSize 是 __m128i 数组的大小(以 128 位块为单位)。smallRemainder 是最后一个 __m128i 元素中有效 unsigned short 元素的数量。当我们检测到这是最后一个元素且短整数的数量不能被 8 整除时,我们需要将最后一个 __m128i 元素中未使用的 short 值设置为 1,以防止除以零的错误。这是一个好习惯,无论返回的是整数类型还是浮点类型,都要对每个最后一个元素执行此操作。
__m128i& CAlphablendDlg::Get128BitElement(
__m128i* ptr,
int bigIndex,
int bigSize,
int smallRemainder)
{
if(bigIndex != bigSize-1) // not last element
return ptr[bigIndex];
else if(smallRemainder==0) // last element
return ptr[bigIndex];
else // last element
{
for(int i=smallRemainder; i<8; ++i)
ptr[bigIndex].m128i_u16[i] = 1;
return ptr[bigIndex];
}
}
我们必须小心地使用 _aligned_malloc 函数来分配我们的 __m128i 数组,以便它们与 128 位 SSE2 指令所需的 16 字节边界对齐。我们计算并存储余数,以防所需的 unsigned short 的数量不能被 8 整除(如前所述)(注意:128 位中有 8 个 unsigned short(16 位数据类型))。
// Calculate the size of 128 bit array
m_fullsize = m_BmpData1.Width * m_BmpData1.Height;
// divide by 8, to get the size in 128bit.
m_arraysize = (m_fullsize) >> 3;
// calculate the remainder
m_remainder = m_fullsize%8;
// if there is remainder,
// add 1 to the 128bit m_arraysize
if(m_remainder!=0)
++m_arraysize;
// since we are using unsigned short (16bit) elements,
// let's muliply the total number of bytes needed by 2.
m_fullsize = (m_arraysize) * 8 * 2;
// Allocate 128bit arrays
m_pSrc1R = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc1G = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc1B = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc2R = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc2G = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
m_pSrc2B = (__m128i *)(_aligned_malloc((size_t)(m_fullsize), 16));
分配完我们的 __m128i 数组后,我们将用图像对象的颜色信息填充它们。我们使用 GetUShortElement 从 __m128i 数组中获取我们的 unsigned short 元素。
// Populate the SSE2 pointers to array
UINT col = 0;
UINT stride = m_BmpData1.Stride >> 2;
for(UINT row = 0; row < m_BmpData1.Height; ++row)
{
for(col = 0; col < m_BmpData1.Width; ++col)
{
UINT index = row * stride + col;
BYTE r = (m_pPixels1[index] & 0xff0000) >> 16;
BYTE g = (m_pPixels1[index] & 0xff00) >> 8;
BYTE b = (m_pPixels1[index] & 0xff);
// assign the pixel color to the 128bit arrays
GetUShortElement(m_pSrc1R, (int)(index)) = r;
GetUShortElement(m_pSrc1G, (int)(index)) = g;
GetUShortElement(m_pSrc1B, (int)(index)) = b;
}
}
最后,我们必须记住在父类的析构函数中使用 _aligned_free 来释放 __m128i 数组。在开始主要编码之前就编写释放代码是一个好习惯。
if( m_pSrc1R )
{
_aligned_free(m_pSrc1R);
m_pSrc1R = NULL;
}
if( m_pSrc1G )
{
_aligned_free(m_pSrc1G);
m_pSrc1G = NULL;
}
if( m_pSrc1B )
{
_aligned_free(m_pSrc1B);
m_pSrc1B = NULL;
}
if( m_pSrc2R )
{
_aligned_free(m_pSrc2R);
m_pSrc2R = NULL;
}
if( m_pSrc2G )
{
_aligned_free(m_pSrc2G);
m_pSrc2G = NULL;
}
if( m_pSrc2B )
{
_aligned_free(m_pSrc2B);
m_pSrc2B = NULL;
}
在运行任何 SSE2 代码之前,我们应该首先确保处理器支持 SSE2。我们可以使用作者编写的 SIMD Detector 类来执行检查。
#include "SIMD.h"
SIMD m_simd;
if(m_simd.HasSSE2()==false)
{
MessageBox(
"Sorry, your processor does not support SSE2",
"Error",
MB_ICONERROR);
return;
}
现在我们来到了文章的重点:使用 SSE2 进行 alpha 混合。使用的公式是 ((SrcColor * Alpha) + (DestColor * InverseAlpha)) >> 8。下面的代码列表有详细的注释。我们使用 _mm_set1_epi16 指令在 __m128i 元素的每个 short 元素中设置相同的 short 值(0)。_mm_mullo_epi16 指令用于将无符号 short 相乘,仅保留 16 位,如果最终结果溢出为 32 位。我们使用 _mm_add_epi16 指令来相加 unsigned short。_mm_srli_epi16 指令用于右移 8 位,以模拟除以 256。我们可以不用除法指令,这是一个福音,因为 SSE2 不支持整数除法。在 SSE2 操作之后,我们需要将数据解包回 ARGB 格式。这种解包会抵消一部分性能提升。
// set alpha 128 bit
__m128i nAlpha128 = _mm_set1_epi16 ((short)(Alpha));
// set inverse alpha 128 bit
__m128i nInvAlpha128 = _mm_set1_epi16 ((short)(255-Alpha));
// initialize the __m128i variables
// so that the compiler shut up about
// uninitialized variables.
__m128i src1R = _mm_set1_epi16 ((short)(0));
__m128i src1G = _mm_set1_epi16 ((short)(0));
__m128i src1B = _mm_set1_epi16 ((short)(0));
__m128i src2R = _mm_set1_epi16 ((short)(0));
__m128i src2G = _mm_set1_epi16 ((short)(0));
__m128i src2B = _mm_set1_epi16 ((short)(0));
__m128i rFinal = _mm_set1_epi16 ((short)(0));
__m128i gFinal = _mm_set1_epi16 ((short)(0));
__m128i bFinal = _mm_set1_epi16 ((short)(0));
for(int i=0;i<m_arraysize;++i)
{
// multiply and retain the result in lower 16bits
src1R = _mm_mullo_epi16 (
Get128BitElement(m_pSrc1R,i,m_arraysize,m_remainder),
nAlpha128);
src1G = _mm_mullo_epi16 (
Get128BitElement(m_pSrc1G,i,m_arraysize,m_remainder),
nAlpha128);
src1B = _mm_mullo_epi16 (
Get128BitElement(m_pSrc1B,i,m_arraysize,m_remainder),
nAlpha128);
// multiply and retain the result in lower 16bits
src2R = _mm_mullo_epi16 (
Get128BitElement(m_pSrc2R,i,m_arraysize,m_remainder),
nInvAlpha128);
src2G = _mm_mullo_epi16 (
Get128BitElement(m_pSrc2G,i,m_arraysize,m_remainder),
nInvAlpha128);
src2B = _mm_mullo_epi16 (
Get128BitElement(m_pSrc2B,i,m_arraysize,m_remainder),
nInvAlpha128);
// Add a and b together
rFinal = _mm_add_epi16 (src1R, src2R);
gFinal = _mm_add_epi16 (src1G, src2G);
bFinal = _mm_add_epi16 (src1B, src2B);
// Use shift right by 8 to do division by 256
rFinal = _mm_srli_epi16 (rFinal, 8);
gFinal = _mm_srli_epi16 (gFinal, 8);
bFinal = _mm_srli_epi16 (bFinal, 8);
// unpack the final results into the 8 pixels
// if possible
int step = i << 3; // multiply by 8
if(i!=m_arraysize-1) // not the last element
{
pixels[step+0] =
0xff000000 |
rFinal.m128i_u16[0] << 16 |
gFinal.m128i_u16[0] << 8 |
bFinal.m128i_u16[0];
pixels[step+1] =
0xff000000 |
rFinal.m128i_u16[1] << 16 |
gFinal.m128i_u16[1] << 8 |
bFinal.m128i_u16[1];
pixels[step+2] =
0xff000000 |
rFinal.m128i_u16[2] << 16 |
gFinal.m128i_u16[2] << 8 |
bFinal.m128i_u16[2];
pixels[step+3] =
0xff000000 |
rFinal.m128i_u16[3] << 16 |
gFinal.m128i_u16[3] << 8 |
bFinal.m128i_u16[3];
pixels[step+4] =
0xff000000 |
rFinal.m128i_u16[4] << 16 |
gFinal.m128i_u16[4] << 8 |
bFinal.m128i_u16[4];
pixels[step+5] =
0xff000000 |
rFinal.m128i_u16[5] << 16 |
gFinal.m128i_u16[5] << 8 |
bFinal.m128i_u16[5];
pixels[step+6] =
0xff000000 |
rFinal.m128i_u16[6] << 16 |
gFinal.m128i_u16[6] << 8 |
bFinal.m128i_u16[6];
pixels[step+7] =
0xff000000 |
rFinal.m128i_u16[7] << 16 |
gFinal.m128i_u16[7] << 8 |
bFinal.m128i_u16[7];
}
// last 128 bit element, not all 16 bit element are filled with valid value
else if(m_remainder!=0)
{
for(int smallIndex=0; smallIndex<m_remainder; ++smallIndex)
{
pixels[i+smallIndex] =
0xff000000 |
rFinal.m128i_u16[smallIndex] << 16 |
gFinal.m128i_u16[smallIndex] << 8 |
bFinal.m128i_u16[smallIndex];
}
}
// last 128 bit element, all 16 bit element are filled with valid value
// Because the remainder is zero
else
{
pixels[step+0] =
0xff000000 |
rFinal.m128i_u16[0] << 16 |
gFinal.m128i_u16[0] << 8 |
bFinal.m128i_u16[0];
pixels[step+1] =
0xff000000 |
rFinal.m128i_u16[1] << 16 |
gFinal.m128i_u16[1] << 8 |
bFinal.m128i_u16[1];
pixels[step+2] =
0xff000000 |
rFinal.m128i_u16[2] << 16 |
gFinal.m128i_u16[2] << 8 |
bFinal.m128i_u16[2];
pixels[step+3] =
0xff000000 |
rFinal.m128i_u16[3] << 16 |
gFinal.m128i_u16[3] << 8 |
bFinal.m128i_u16[3];
pixels[step+4] =
0xff000000 |
rFinal.m128i_u16[4] << 16 |
gFinal.m128i_u16[4] << 8 |
bFinal.m128i_u16[4];
pixels[step+5] =
0xff000000 |
rFinal.m128i_u16[5] << 16 |
gFinal.m128i_u16[5] << 8 |
bFinal.m128i_u16[5];
pixels[step+6] =
0xff000000 |
rFinal.m128i_u16[6] << 16 |
gFinal.m128i_u16[6] << 8 |
bFinal.m128i_u16[6];
pixels[step+7] =
0xff000000 |
rFinal.m128i_u16[7] << 16 |
gFinal.m128i_u16[7] << 8 |
bFinal.m128i_u16[7];
}
}
基准测试结果

下面列出了每个基准测试中使用的公式


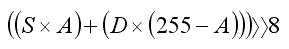
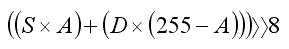
这是在 2.93 Ghz 的 Intel i7 870 上进行 1000 次 alpha 混合的计时。性能特征与上一篇文章中发布的不同,因为基准测试是在不同的 PC 上进行的。之前使用的 PC 已“退役”,不再服务于这个世界。

VS2010 Release mode(optimization disabled)(Lower is better)
Author code
Unoptimized Code : 4679 milliseconds
Optimized Code : 2108 milliseconds
Optimized Code with Shift : 1931 milliseconds
SSE2 Optimized Code : 862 milliseconds (works for all image width)
Yves Daoust's code
C version : 1923 milliseconds
MMX 1 : 1888 milliseconds
MMX 2 : 1355 milliseconds (image width must be even)
SSE : 762 milliseconds (image width must be multiple of 4)
VS2010 Release mode(optimization enabled)(Lower is better)
Author code
Unoptimized Code : 3324 milliseconds
Optimized Code : 1378 milliseconds
Optimized Code with Shift : 802 milliseconds
SSE2 Optimized Code : 406 milliseconds (works for all image width)
Yves Daoust's code
C version : 604 milliseconds
MMX 1 : 213 milliseconds
MMX 2 : 167 milliseconds (image width must be even)
SSE : 104 milliseconds (image width must be multiple of 4)
下面是我们与未优化版本相比获得的速度提升倍数。但将 SSE2 的速度提升与第二名(带有移位优化的代码)进行比较,速度提升仅为 2.2 倍,而不是我们预期的 8 倍。那么 SSE2 加速所需的内存消耗是多少?每个颜色通道 2 字节,而不是 1 字节。原始实现需要 4 字节来存储一个颜色像素 (ARGB)。(使用 4 字节是因为处理器加载和存储 32 位数据比 24 位数据更快,这可能需要将其移位到正确的 32 位边界才能加载到 32 位寄存器中)。SSE2 版本需要 6 字节来存储一个颜色像素 (RGB)(因为每个颜色通道使用两个字节)。单独的 alpha 通道不存储,因为它们不被使用。SSE2 版本需要多 50% 的内存来执行其魔术。
(Higher is better)
Unoptimized Code : 1x
Optimized Code : 2.2x
Optimized Code with Shift : 2.4x
SSE2 Optimized Code : 5.4x
结论
我们使用 SSE2 将之前的最快性能提升了两倍。速度提升并不显著。这可能不值得付出大量的额外努力和编写难以理解的代码。为了实现更好的可读性,我们可以使用dvec.h头文件中列出的向量类。这个向量类支持 -, +, *, /, 等运算符重载。欢迎提出任何进一步提高性能的建议。我们可以通过结合使用 OpenMP 或 并行模式库 (PPL) 和 SSE2 来提高性能。但这将是另一天的文章。任何有兴趣了解关于使用 OpenCL 进行 alpha 混合的未来文章的读者,请在下方给我留言。OpenCL 是一种异构技术;OpenCL 内核可以在 CPU 或 GPU 上运行。
参考文献
- SIMD 检测器
- Agner Fog 的《C++ 软件优化》
- Visual Studio 11 Express 预览版中的自动向量化
- Visual C++ 11 中的自动向量化器 (MSDN)
- 英特尔® C++ 编译器自动向量化指南
历史
- 2011 年 11 月 17 日:添加了 Yves Daoust 的 MMX 和 SSE 代码及基准测试结果
- 2011 年 11 月 14 日:首次发布
