蒙提霍尔悖论图解
4.59/5 (14投票s)
一个说明蒙提霍尔悖论的 Window Forms 应用程序。
如果您的实验需要统计数据,那么您应该做一个更好的实验。
- 欧内斯特·卢瑟福
什么是蒙提霍尔悖论?
如果您看过电影《21 点》,您可能还记得影片开头有一个场景,一位讲师向他的学生提出了以下逻辑谜题:
假设您参加一个游戏节目,可以选择三扇门:一扇门后面是汽车,另外两扇门后面是山羊。您选择一扇门,主持人知道门后面的东西,他打开另一扇后面是山羊的门。然后他问您是否要重新考虑并选择另一扇门。更换您的选择对您有利吗?
学生同意交换选择,并且他是正确的。他的获胜几率将从 1/3 提高到 2/3。您可以在此处观看电影片段,维基百科对此被称为蒙提霍尔问题(以电视节目主持人命名)的悖论有相当全面的解释。
我将不再在这里重复这个问题的解决方案。它在网上各种来源中都有很好的解释。尽管如此,当理论论证有时不足以解决问题时,这个悖论仍会引发激烈的讨论——人们可能坚持认为这样的事情根本不可能发生。
这就是为什么我决定编写一个简单的 Windows Forms 应用程序,该程序接受门数(让我们展示任何门数的统计数据,而不仅仅是三扇门,主持人将不得不打开 N-2 扇后面有山羊的门)和迭代次数作为输入,并显示选择更换最初选择的玩家的几率。为了清晰起见,我们将假设玩家选择更换他们的最初选择,因此所有几率和概率都将根据选择更换策略进行计算。
这么多取决于主持人!
为了让程序更具说明性,我决定展示的不仅仅是蒙提霍尔的情况。由于许多人坚持认为更换门不会增加玩家的几率,我想展示什么时候这是真的:当主持人随机打开门,冒着揭示汽车的风险时,这是真的。但是,如果主持人知道汽车在哪里,并且故意只打开有山羊的门,那么更换门对玩家有利——门的数量越多,更换后获胜的几率就越高。
消息灵通的主持人
让我们从经典的蒙提霍尔情况开始:主持人知道门后面是什么,并且只打开有山羊的门。让我们为幸运的门和玩家的最初选择进行随机选择。
int luckyDoor = random.Next(0, numberOfDoors);
int doorSelectedByPlayer = random.Next(0, numberOfDoors);
现在,我们应该为主持人做一个选择,对吗?嗯,实际上我们不需要。他没有太多选择的自由,即使他有选择,也无关紧要。如果玩家没有选择到后面是汽车的门,那么主持人将不得不打开所有剩余的有山羊的门,留下后面是汽车的门不开。在这种情况下,更换我们最初的选择将使玩家获胜。但是,如果玩家第一次尝试运气不错,那就是他的坏运气,因为正如我们前面提到的,我们评估的是玩家更换最初选择的策略;因此,无论主持人选择打开哪些门,玩家都会选择另一扇门并揭示山羊。以下是有消息灵通的主持人的算法:
if (luckyDoor == doorSelectedByPlayer)
{
// Player guessed right on the first attempt,
// so he will lose after the swap
return GameResult.Goat;
}
else
{
// Player missed on the first attempt,
// so he will win the car after the swap
return GameResult.Car;
}
不明就里的主持人
对于不明就里的主持人来说,情况要复杂一些,因为可能会发生主持人随机选中后面是汽车的门。显然,这种情况会破坏游戏——我们评估的是当主持人揭示山羊时的获胜几率。因此,不明就里的主持人游戏规则要求在主持人打开玩家未选择的 N-2 扇门时揭示汽车的情况下,重新进行游戏。在这种情况下,与经典的蒙提霍尔情况不同,必须考虑主持人的选择。
int luckyDoor = random.Next(0, numberOfDoors);
int doorSelectedByPlayer = random.Next(0, numberOfDoors);
int doorNotSelectedByHost = random.Next(0, numberOfDoors - 1);
if (luckyDoor == doorSelectedByPlayer)
{
// Player guessed right on the first attempt,
// so he will lose after the swap
return GameResult.Goat;
}
else
{
// Player missed on the first attempt, check if host opened the lucky door
if (luckyDoor < doorSelectedByPlayer && luckyDoor != doorNotSelectedByHost ||
luckyDoor > doorSelectedByPlayer && luckyDoor != doorNotSelectedByHost + 1)
{
return GameResult.Discarded;
}
else
{
// Player will win the car after the swap
return GameResult.Car;
}
}
让我们仔细看看上面的代码。如果玩家最初选择了一扇后面是汽车的门,他最终还是会得到一头山羊。当他第一次选择一扇后面是山羊的门时的情况需要进一步检查。我们不是让主持人打开 N-2 扇门,而是简单地选择剩余的 (N-1) 扇未选择的门中的一扇 *不* 打开。这是等效的。主持人可能不会打开玩家选择的门,所以我们需要在他的门集中为玩家的门设置一个“空位”。当汽车位于主持人打开的门后面时(即 luckyDoor != doorNotSelectedByHost),游戏结果将被丢弃(并重玩游戏)。如果游戏未被丢弃,那么玩家在更换最初选择后将成为赢家。
关于随机数生成和线程的说明
尽管我喜欢实现独立的类(尤其是在这样一个简单的例子中),但我不得不创建一个 Random 对象实例,并在实现了不同主持人策略的类(GameWithInformedHost 和 GameWithCluelessHost)中使用它。在每次迭代中创建一个随机生成器太慢了,而且由于使用了相同的种子,导致随机性较差。在类之间共享一个 Random 对象实例使得应用程序运行速度更快。
最初,我曾考虑使用多个线程运行模拟游戏并持续报告进度,但在测试了在现代机器上运行这些算法的速度有多快之后,我得出结论,多线程只会增加代码的复杂性,而实际上没有任何好处。运行一百万次游戏只需要几秒钟,足以产生具有三位有效数字的结果。
同时进行百万次蒙提霍尔游戏
蒙提霍尔应用程序可以模拟任何次数的迭代和任何数量的门。以下是使用三扇门和一千万次迭代产生的结果:
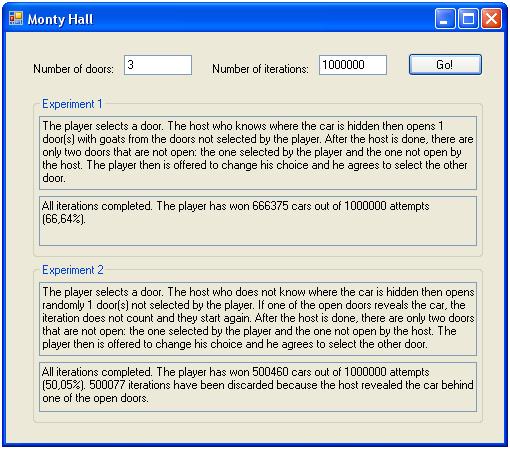
另外,如果汽车在一亿扇门后面,结果是这样的:
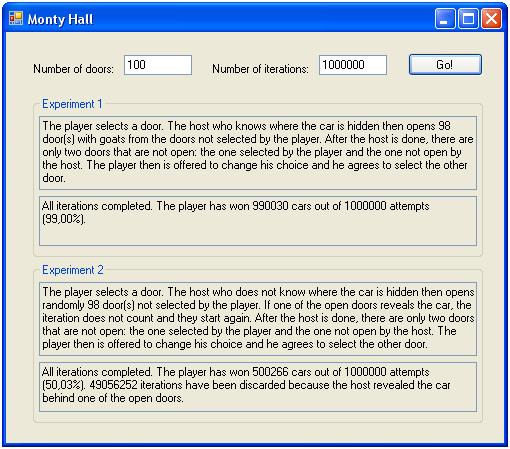
正如您所见,在消息灵通的主持人的情况下,增加门的数量使更换玩家最初的选择成为必须:这是要么全有要么全无。而且,如果主持人不明就里,玩家的几率仍然是 50/50。
