C# 中的简单 QuadTree 实现

• 下载演示项目 - 10.81 KB
• 下载源代码 - 19.82 KB

引言

QuadTree 是一种空间划分策略，用于对二维空间数据之间的关系进行查询，例如地理信息系统 (GIS) 中的坐标，或视频游戏中的对象位置。例如，您可能需要了解地图上某个区域内的所有对象，测试对象是否被摄像机看到，或优化碰撞检测算法。

QuadTree 之所以得名，是因为它将区域递归地划分为四个部分，叶节点包含对空间对象的引用。查询 QuadTree 的功能是遍历与查询区域相交的树节点。

OctTree 是用于三维问题的类似结构。

有关 QuadTree 和其他空间索引方法的演示和变体的精湛合集，请参阅 Frantisek Brabec 和 Hanan Samet 的网站，或使用本文末尾的参考文献。

背景

存在许多 空间划分 方法，每种方法都旨在提供一种有效的方式来确定项目在空间域中的位置。例如，数据库查询可以被视为一个图形问题。考虑一个包含出生日期和收入的数据库查询：一个查询所有年龄在 35 到 50 岁之间且收入在每年 30,000 到 60,000 之间的人，与查询温哥华市的所有餐馆相同：它们都是二维空间查询。

几种空间索引方法在时间和空间上更有效，并且易于推广到更高维度。但是，QuadTree 专门用于二维领域，并且易于实现。

算法

QuadTree 的总体策略是构建一个树结构，将一个区域递归地划分为四个部分，或称为 Quad。每个 Quad 可以根据需要进一步划分。前提是您必须知道要覆盖的区域的边界；基本算法不适用于添加或删除正在考虑的区域而不重新生成索引。

插入

当一个项被插入到树中时，它会被插入到包含该项位置（或空间索引）的 Quad 中。每个 Quad 都有一个最大容量。当超过该容量时，Quad 会分裂成四个子 Quad，成为父 Quad 的子节点，并将这些项重新分布到 QuadTree 的新叶节点中。某些变体将最大容量设置为一，并一直细分，直到每个叶节点最多包含一个项（自适应 QuadTree）。

查询

要查询 QuadTree 中位于特定矩形内的项，需要遍历该树。测试每个 Quad 是否与查询区域相交。

1. 不相交的 Quad 不会被遍历，从而可以快速排除大量空间索引区域。

   

2. 完全包含在查询区域内的 Quad 的子树将被添加到结果集中，而无需进一步的空间测试：这使得大型区域可以在没有进一步昂贵操作的情况下被覆盖。

   

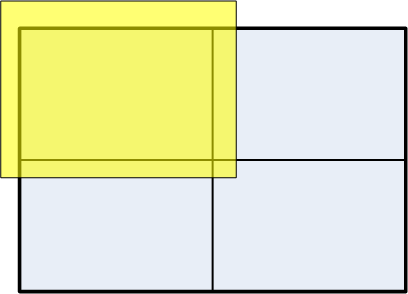
3. 相交的 Quad 会被遍历，并递归地测试每个子 Quad 是否相交。

   

4. 当找到一个没有子 Quad 的 Quad 时，其内容会单独测试是否与查询矩形相交。

其他操作

QuadTree 上的其他操作可能包括

1. 删除：从 QuadTree 中删除一个对象，移除空的 Quad
2. 合并：合并两个 QuadTree，重新构建索引
3. 最近邻：对于更高级的空间索引，查询可以询问给定对象的最近邻。一种简单的实现方法是取对象的边界矩形，并根据邻近度增加其大小。结果集中的对象将按距离递增的顺序排序。

这些操作未在此代码中演示。

变体

此 QuadTree 实现具有以下变体

QuadTree 已被修改为索引具有矩形边界而不是点的项。这使其可以与线和多边形一起使用。

• 在插入时，会创建新的 Quad，直到没有 Quad 能够容纳项的矩形。即：该项被插入到能够容纳它的最小 Quad 中。
• Quad 没有最大项数，但有一个最小 Quad 大小（这是为了避免在某个项的面积非常小时导致树结构大量增长）。
• 由于项存储在哪个 Quad 中与项的大小有关，因此叶节点和父节点都存储项。
• 如果存在许多大型项，QuadTree 的性能将受到严重影响。
• 当大多数项的大小接近最小 Quad 大小时，Quadtree 的性能最佳。

编写完此代码后，我发现此特定变体与“MX-CIF QuadTree”非常相似。

注意：QuadTree 上还有其他操作，例如删除节点或查找最近邻。这些在本实现中不支持。

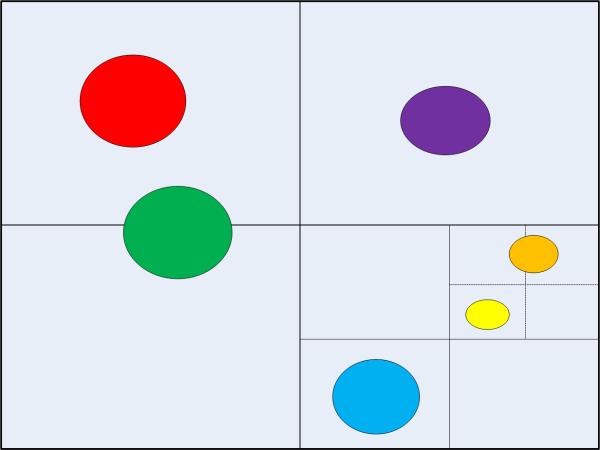
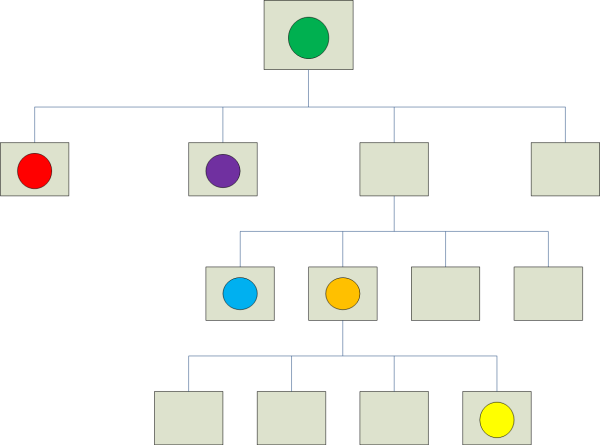
以下两张图展示了 QuadTree 与树结构的空间关系。彩色区域表示空间域中的对象。完全位于 Quad 中的对象显示在其最小的包含 Quad 的树结构中。可以看到，绿色形状由于与最高层 Quad 中的两个相交且两者都无法容纳它，因此被放置在根 Quad 中。红色和紫色的形状被放置在一级子节点中，因为它们是最大的包含 Quad。蓝色形状与橙色形状一样，处于三级。黄色形状处于四级。此树是自适应的，因为它不会在请求插入之前创建 Quad。

Using the Code

QuadTree 类是一个泛型类。泛型参数有一个限制，它必须继承自定义了 Rectangle 属性的 IHasRect 接口。创建 QuadTree 需要一个区域，演示应用程序使用主窗体的 ClientRectangle。

QuadTree<Item> m_quadTree = new QuadTree<Item>(this.ClientRectangle); 

向 QuadTree 插入项通过左键单击完成，查询 QuadTree 中的项通过右键拖动完成。

private void MainForm_MouseUp(object sender, MouseEventArgs e) 
{ 
    if (m_dragging && e.Button== MouseButtons.Right) 
    { 
        m_selectedItems = m_quadTree.Query(m_selectionRect);
        m_dragging = false;    
    } 
    else 
    { 
        Random rand = new Random(DateTime.Now.Millisecond); 
        m_quadTree.Add(new Item(e.Location, rand.Next(25) + 4)); } Invalidate(); 
    }
}

运行演示应用程序，并在客户端矩形内的任意位置左键单击：会在单击点插入一个随机大小的对象。右键单击并拖动：会创建一个选择矩形。释放鼠标按钮：使用选择矩形查询 QuadTree。QuadTree 渲染器以随机颜色绘制 QuadTree 节点和 QuadTree 中的对象。它还会绘制选择区域并突出显示选定的节点。

性能

QuadTree 的性能有两个组成部分：插入和查询。插入可能非常昂贵，因为它涉及对每个要插入的项进行多次相交测试。测试次数取决于区域的大小（QuadTree 的根）和配置的最小 Quad 大小。这两个数字需要针对每个应用程序进行调整。将大量项加载到 QuadTree 中（批量加载或索引）通常会非常占用 CPU 资源。此开销可能不可接受；请考虑将 QuadTree 结构存储在磁盘上（本文未涵盖）。

QuadTree 的设计旨在比迭代查询空间域的速度更快，但索引的性能取决于对象在域中的分布。如果项聚集在一起，树往往会在一个分支中有许多项，这就违背了能够裁剪大区域并减少相交测试次数的策略。最坏情况的性能发生在所有对象都位于一个与最小 Quad 大小相同的微小簇中时；在这种情况下，QuadTree 的性能将比仅仅迭代所有对象的性能稍差。

如果项在空间域中均匀分布，性能约为 O(n*log n)。

关注点

• 泛型实现；允许您将其与实现 IHasRect 接口的任何类一起使用。
• 用于绘制节点的颜色存储在哈希表中；允许 Quad 在屏幕上的颜色在 QuadTree 的生命周期内保持不变。
• 在 QuadTreeRenderer 类中，请注意用于绘制 QuadTreeNodes 的匿名委托；它允许在不向类添加特定代码的情况下测试和可视化 QuadTree。

参考文献

• H. Samet, The Design and Analysis of Spatial Data Structures, Addison-Wesley, Reading, MA, 1990. ISBN 0-201-50255-0
• H. Samet, Applications of Spatial Data Structures: Computer Graphics, Image Processing, and GIS, Addison-Wesley, Reading, MA, 1990. ISBN 0-201-50300-0。
• Mark de Berg, Marc van Kreveld, Mark Overmars, Otfried Schwarzkopf, Computational Geometry: Algorithms and Applications, 2nd Edition, Springer-Verlag 2000 ISBN: 3-540-65620-0

历史

• 初始版本包含区域以及简单的插入和查询操作，以及演示应用程序