(AI) 滑块拼图解决方案分析器
4.86/5 (19投票s)
我的解决方案算法、已实现程序和总结结果的详细信息。
目录
1. 引言
基本搜索算法构成了人工智能 (AI) 的基础。因此,理解其概念并能够实现它们对于进行更高级的AI研究至关重要。
在本报告中,我将解释我的解决方案算法、已实现程序以及我得出的结果的详细信息。
2. 滑动拼图的AI搜索方法
几乎所有与AI相关的最基本知识都可以在Steward Russell和Peter Norvig的著作《人工智能:一种现代方法》[1]中找到。
在这个带回家作业中,我们被要求在可调节大小的“滑动拼图”上实现广度优先搜索(BFS)、深度优先搜索(DFS)、迭代加深深度受限DFS(IDFS)以及带有“错位图块启发式”(A* Mis)和“总曼哈顿距离启发式”(A* Man)的A*算法。在这些算法中,A*、IDFS和BFS提供最优路径,而DFS在检测最短解决方案路径方面不是最优的。
滑动拼图需要一个代理来解决问题,即我们在这次带回家考试中编写的程序。它是一个确定性、情景式且完全可观察的问题。换句话说,它是计算机环境中实现的最简单的问题之一。然而,滑动拼图具有非常循环的结构。最小的循环只由两步构成,即向前和向后移动图块。尽管找到这个两步循环非常容易,但一些更大的循环却不那么容易检测到。
在解决此拼图时,应构建已打开状态的历史记录。否则,搜索空间将无限扩展,解决即使是最简单的拼图也变得繁重,有时甚至不可能。我将该历史记录保存在 C# 的 Sorted List 结构中。它基本上使用键对插入的节点进行排序,当要求检索节点时,使用该键请求节点。因此,历史记录中的搜索变得非常高效和快速。
进一步参考,3x3滑动拼图有181,440个可解状态,4x4的有约13万亿步,而5x5的有约1025个状态。因此,3x3几乎是唯一一个所有算法都能在合理时间内解决的。
解释代码的最佳方式是绘制其流程图。因此,我将用流程图解释所使用的算法。希望它们能使本报告更容易理解,更清晰。
我将在本报告的相应部分更详细地解释我的方法。
2.1. 已实现的无信息搜索方法
顾名思义,无信息搜索不知道访问哪个后继节点会更有益。BFS、DFS和IDFS是本次带回家考试中实现的方法。
2.1.1. 广度优先搜索 (BFS)
除了历史记录之外,实现的算法与[1]中解释的完全相同。BFS算法也可以在没有历史记录的情况下工作,但由于滑动拼图的循环结构,搜索空间变得无界。因此,在找到解决方案之前内存被填满变得极有可能。在算法测试中,发现BFS无法在合理的时间内(2-3分钟)解决超过15步的拼图。然而,在实现历史记录之后,它可以在合理的时间内达到25步。我的BFS总是给出最优(最短)解决方案路径。

2.1.2. 深度优先搜索 (DFS)
DFS通常以递归方式实现。我也实现了递归版本。但是,在我的代码的最终版本中我没有使用它。迭代版本仍然可以在源代码中找到,但可执行程序使用非递归DFS。它与BFS几乎完全相同,除了它使用堆栈而不是队列。在3x3问题中,如果运气好,DFS可以在几百步内找到解决方案。但大多数情况下,它会搜索几乎整个搜索空间,解决3x3问题大约需要一分钟。由于4x4及更大拼图具有更多状态,可以说DFS无法在合理的时间内找到解决方案,除非用户运气好。

2.1.3. 迭代加深深度受限深度优先搜索 (IDFS)
我以递归和非递归形式实现了IDFS。但由于易于理解和更好地跟踪代码,最终程序中只使用了非递归算法。

IDFS有一个限制值,限制从1开始。当第一次迭代没有找到解决方案时,限制增加1,并再次开始深度受限DFS。限制增加直到达到一个阈值。在我的程序中,这个阈值大于200,000,以便对于3x3的情况总是能找到解决方案。实际上,在真实情况下限制永远无法达到这个值,因为当深度限制变大时,搜索整个搜索空间需要很长时间。实际上,要搜索指定深度,IDFS比BFS花费更长的时间,因为IDFS迭代地搜索所有级别。但IDFS的好处是它需要的内存非常少。存储近似于深度限制的节点数量就足够了。
为了最优性,在我的IDFS中,我需要保留历史记录,但这次历史记录略有修改,如图3所示。现在,IDFS总是给出最优解。因为如果在一个后继节点在历史记录中找到,但该后继节点的深度小于历史记录列表中的深度,它就会被推入堆栈,并且历史记录会被更新。
2.2. 已实现的有信息搜索方法
有信息搜索方法可以预测打开哪个节点会更有益。在这个问题中,一个节点的代价可以认为是它的深度,因为每次移动只花费1。
A* 算法实现了两种启发式函数。其中一个计算错位图块的数量,另一个计算所有图块到其目标状态的总曼哈顿距离。两种启发式函数都是可采纳的,即小于实际解决成本。但曼哈顿距离比错位图块更能接近剩余步数的近似值。
2.2.1. 带错位图块启发式算法的A* (A* Mis)
首先,A* 算法使用总错位图块启发式实现。它类似于 BFS 算法,并对 IDFS 算法中的历史记录进行了改进。但是,这次,具有最小 (成本 + 启发式) 函数的项目从列表中弹出。该列表以排序方式维护,因此访问最小元素比检查列表中的所有元素快得多。我的实现的带错位图块启发式算法的 A* 总是给出最优结果。它明显快于 BFS、DFS 和 IDFS。我将首先解释带曼哈顿距离的 A*,然后给出 A* 算法的流程图,因为它对于两种启发式函数都是相同的,只是启发式的计算方式不同。
2.2.2. 带曼哈顿距离启发式算法的A* (A* Man)
带有曼哈顿距离启发式算法的A*在所有实现的算法中提供了最最优的结果。它存储的节点非常少,以极少的扩展步骤和时间找到解决方案。通过该算法,证明了曼哈顿距离启发式算法在滑动拼图解决方案中的效率。
实现的A*算法的流程图如下

3. 已实现的程序
我用 C# 实现了我的程序。作为 C# 的一个不同之处,我们可以说它不允许自定义类使用指针和指针算术。然而,它的预定义结构允许用户即使没有指针也能完成工作。例如,我们可以创建父节点而不是创建反向指针,并且可以跟随父节点而不是跟随反向指针,即,一个节点在其结构中存储另一个作为其祖先的节点。此外,许多实现,如 Sorted List,在 C# 中是默认提供的。此外,微软提供了可能是编写程序的最佳 IDE,Visual Studio。
该程序被分为许多类,用于节点、拼图和不同的算法。如果一个问题可以表示为滑动拼图,我的程序就可以解决它。
我实现的程序启动时如下所示

用户可以创建自己的拼图,让PC创建拼图,加载现有拼图,甚至立即加载蒙特卡罗运行。请注意,蒙特卡罗数据必须首先生成。所以让我们从自动拼图生成器开始。它通过避免循环,在指定真实距离处生成滑动拼图。但它以深度优先的方式进行,有时求解算法可以找到比期望步数更短的解决方案路径。但最终,拼图是根据其真实步数而不是期望的创建步数进行检查的。可以通过单击主GUI中的“为我创建拼图”按钮打开自动拼图生成器。

首先,必须选择拼图大小,然后是期望的真实步数。拼图将自动生成并显示。如果您不喜欢该拼图,只需单击“生成新拼图”按钮。您可以重复操作,直到满意为止。要保存拼图,请单击“我喜欢它,保存拼图”按钮。它将允许您选择保存拼图的名称和位置。拼图以 XML 格式保存。我们可以打开 XML 并指定任何自定义状态。但用户必须确保拼图的可解性。否则,我的程序还具有手动拼图生成器。自动拼图生成器上的最后一件事是,它会生成包含100个拼图的蒙特卡罗数据,这些拼图具有指定的步数和大小。它不会显示它们,但它们只是随机状态。用户可以打开保存的蒙特卡罗数据文件并检查它。但请务必不要修改它。

在创建蒙特卡罗数据时,进度会显示在窗体的顶部栏中。但是,如果您想取消蒙特卡罗生成,只需关闭自动拼图生成器即可,并且不会保存任何内容。您可以同时打开多个拼图生成器,因为它们独立于拼图求解器工作。
我们可以用它来创建自定义拼图。手动拼图生成器会完成这项工作。选择大小后,只需单击带数字的按钮即可更改状态。用户可以保存他/她喜欢的任何状态。自定义拼图的所需真实步数将显示为-1。




生成拼图后,用户可以将其加载到主GUI。只需单击“加载已保存的拼图”按钮即可加载已生成的拼图。一旦拼图加载,拼图规格将显示在主GUI屏幕上。最初它将打开“我将解决它”选项。此选项未实现。它只是为了好玩,让用户单击按钮并尝试自己解决拼图。在我的程序中,拼图解决数据也保存在拼图保存文件中。因此,如果一个生成的拼图被解决一次,它将显示以前解决的统计数据。无论如何,用户可以随意解决拼图。当加载一个大型拼图时,GUI会自动调整大小。GUI按钮的放置在某些计算机上可能会发生偏移。但GUI可以轻松调整大小。
为了让程序解决拼图,请点击单选按钮中的算法,然后点击“解决”按钮。不同的算法,按钮会以不同的颜色显示。


当一个谜题被解决后,其解决方案统计数据和解决方案步骤会保存到其创建的XML文件中。一个保存文件的示例如下:
<?xml version="1.0" encoding="utf-8"?>
<AIMehmutluSlidingPuzzleSaveFile>
<Puzzle.000>
<Size>3</Size>
<State>1,2,3,7,4,5,0,8,6</State>
<DesiredOptimalSolutionStep>-1</DesiredOptimalSolutionStep>
<SolvedAlgorithms>
<BFS>
<Solved>T</Solved>
<SolutionTime>7</SolutionTime>
<NoOfStoredNodes>18</NoOfStoredNodes>
<NoOfNodeExpansion>26</NoOfNodeExpansion>
<SolutionStep>4</SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
<Node1>1,2,3,0,4,5,7,8,6</Node1>
<Node2>1,2,3,4,0,5,7,8,6</Node2>
<Node3>1,2,3,4,5,0,7,8,6</Node3>
<Node4>1,2,3,4,5,6,7,8,0</Node4>
</SolutionNodes>
</BFS>
<DFS>
<Solved>F</Solved>
<SolutionTime></SolutionTime>
<NoOfStoredNodes></NoOfStoredNodes>
<NoOfNodeExpansion></NoOfNodeExpansion>
<SolutionStep></SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
</SolutionNodes>
</DFS>
<IDFS>
<Solved>F</Solved>
<SolutionTime></SolutionTime>
<NoOfStoredNodes></NoOfStoredNodes>
<NoOfNodeExpansion></NoOfNodeExpansion>
<SolutionStep></SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
</SolutionNodes>
</IDFS>
<AStarMisplacedTiles>
<Solved>F</Solved>
<SolutionTime></SolutionTime>
<NoOfStoredNodes></NoOfStoredNodes>
<NoOfNodeExpansion></NoOfNodeExpansion>
<SolutionStep></SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
</SolutionNodes>
</AStarMisplacedTiles>
<AStarManhattan>
<Solved>F</Solved>
<SolutionTime></SolutionTime>
<NoOfStoredNodes></NoOfStoredNodes>
<NoOfNodeExpansion></NoOfNodeExpansion>
<SolutionStep></SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
</SolutionNodes>
</AStarManhattan>
</SolvedAlgorithms>
</Puzzle.000>
</AIMehmutluSlidingPuzzleSaveFile>
在上面保存的文件示例中,谜题生成数据位于最顶部。此外,还为不同的求解器算法预留了特定位置。一旦某个算法解决了谜题,其统计数据将保存到相应的空间中。例如,上面的数据已通过 BFS 解决。BFS 统计数据已保存到相应空间,解决方案路径也保存为一系列状态。上面的谜题只是一个单独的谜题。在蒙特卡罗数据中,有100个谜题,每个谜题命名为 Puzzle.(编号)。例如,Puzzle.024 指的是蒙特卡罗数据中的第24个谜题。
因此,如果我们将已解决的拼图加载到主GUI,它将显示之前的解决方案统计数据。最初显示的是拼图的初始节点。如果拼图已解决,用户可以通过单击带有前进和后退箭头的按钮来查看解决方案路径。此外,单击PLAY按钮将自动播放上一步解决方案。播放可以随时停止;可以手动前进或后退步骤。一旦解决方案步骤完成,播放选项将显示目标状态两秒钟,然后重新显示初始状态。





如果加载了一个非常难的拼图,而您厌倦了等待解决方案,您只需按下“停止求解器”按钮。在GUI上工作时,按钮将被启用或禁用,以避免程序工作顺序中的冲突。


蒙特卡罗运行按顺序进行。首先用BFS、DFS、IDFS、A* Mis和A* Man算法解决第一个拼图,然后解决第二个拼图。它对所有100个拼图都如此。用算法解决后,GUI上会显示一个已解决的消息。这可以在图20中看到。但请注意,BFS、IDFS、A* Mis和A* Man在浅层步骤中解决拼图的速度比DFS快得多。所以它们的消息显示和删除都很快。因此,只有在等待算法解决时,消息才会被注意到。例如,在图20中,当用DFS解决时,会显示“拼图已用BFS解决”。而其他算法的消息会很快跳过,因为它们解决得很快。这不是一个错误。
A* Man 算法非常好。除非拼图被极度打乱,否则它可以非常快速地解决拼图。在图26中,显示了A* Man 的能力。一个10x10的拼图在58个真实步骤中在7秒内解决。

4. 已实现的辅助程序
4.1. C# 中的数据转换器
为了在 MATLAB 上绘制性能图,需要使用 MATLAB 提取解决方案统计数据。为了简化 MATLAB 中的工作,我编写了一个小型独立程序,用于将 XML 格式的已解决蒙特卡罗数据转换为更简单的文本格式。我编写了相同转换程序的各种变体,用于算法比较和大小比较。使用 A* 进行的大小比较并不太具有解释性。我将在下一节中详细说明,因此我还使用 BFS 进行了大小比较。



在解决了各种100个拼图的蒙特卡罗数据之后,XML文件通过上述程序转换为文本。在迷你程序中,将解码后的数据文件的未来名称写入文本文件,然后单击GUI上唯一可用的按钮。它会要求您找到XML文件中的已解决蒙特卡罗数据。一旦提供了XML文件,它将在可执行文件所在的目录中生成解码后的文本文件。一旦文本文件准备好,它们将被馈送到MATLAB函数中,用于绘制数据。
4.2. MATLAB 中的数据绘图器
为了获得漂亮的图表,我编写了 MATLAB 函数,它们将获取多个蒙特卡罗运行的解码文本数据并提取信息。函数只会要求提供包含蒙特卡罗运行的目录。最后,它将给出图表。对于不同的数据运行,MATLAB 函数中需要进行小的参数更改。包含 MATLAB 函数的 MATLAB .m 文件也已在本报告提交的文件夹中提供。由于 MATLAB 函数相当冗长,因此本报告中不会提供代码。
5. 结果
5.1. 算法分析
为了比较算法,创建了100个3x3拼图批次,真实步长分别为5、10、15、20和25。总共500个拼图使用五种不同算法解决,即2500个解决方案作为数据库。如“带回家定义”表中所述,所有创建的拼图并非都处于期望的步长,因为它们是以深度优先方式创建的。但它们被精细地分为真实步长数组,并对真实步长进行数据检查。生成的数据步长从4到25不等(4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、20、21、22、23、24、25)。所有数据都以蓝色点绘制在MATLAB图表中。但是当真实步长的样本数量超过设置为20的阈值时,相同真实步长的集合被认为是可信赖的集合,并取平均值,并在图表上用红色圆圈标记。
本页其余部分故意留白,以便在一个页面中显示算法结果。
BFS算法对所有方面都呈现指数级结果。请注意存储节点数据中的饱和现象。原因是 BFS 算法中使用了历史记录。当历史记录几乎覆盖整个搜索空间时,只有一小部分扩展节点可以存储,因为所有其他节点都已在历史记录中,即它们已在较低级别访问过。



对于DFS,请注意步长大小并不那么重要。DFS要么搜索整个搜索空间,要么非常快地找到目标。但当数据取平均值时,DFS的性能几乎相同。这个结果正如预期。在比较图中,DFS似乎不如其他算法,但这主要是因为我们通常在非常低的步长解决方案下应用数据。如果我们给出更高步长的拼图,BFS的解决时间会持续增加,但DFS的平均解决时间仍然几乎是搜索整个搜索空间所需时间的一半。同样适用于其他属性。



与BFS相比,IDFS需要更长的时间才能找到解决方案。在IDFS中,节点扩展率和解决时间都是指数级的,并且比BFS差。然而,在存储节点方面,IDFS具有极大的优势。它只存储与找到解决方案的深度数相近的节点。因此,对于真实步数的拼图,内存使用量几乎与步数呈线性关系。IDFS比BFS需要更多的CPU功率,但可以节省RAM。
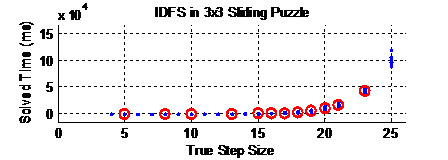


有信息搜索在整体性能上比无信息搜索表现得更好。尽管IDFS存储的节点数量较少,但其解决时间永远无法与A*解决时间竞争。A*的统计数据仍然呈指数级增长。但存储节点和扩展节点的水平远优于BFS和DFS。我们可以很容易地得出结论,有信息搜索比无信息搜索好得多。



在A*曼哈顿距离数据中,我们可以得出结论,更好的启发式函数是那些给出更接近实际最优解代价的函数。A*曼哈顿距离案例中的解决时间并没有提供太多信息。我注意到数据中出现了一些奇怪的周期性增长。这可能是由于操作系统的线程管理。但是扩展节点和存储节点数据正确地呈现了指数趋势。A* Man证明了它在滑动拼图解决方案中的有效性。



5.2. 拼图尺寸分析
为了观察拼图尺寸对同一算法的影响,以特定真实步长创建了各种尺寸(3x3,4x4…10x10)的100个拼图批次。它们使用一种算法解决并绘制统计数据。所有数据都以蓝色点绘制在MATLAB图表上。但是当真实步长和指定尺寸的样本数量保持在设置为20的阈值以上时,相同真实步长的集合被认为是可信赖的集合,并取平均值,并在图表上用红色圆圈标记。
生成的拼图并不总是处于期望的步数。因此,我只是丢弃了不在期望步数的数据。因此,特定步数和尺寸下的集合大小从100减少到更小的数字。在小拼图尺寸下,下降非常剧烈。但请注意,可靠数据用红色标记。
我首先在20步下用A* Man进行了实验。我无法得出有意义的结果,于是重复了35步下A* Man的测试。但仍然无法得出合理的解释。最后,我用10步拼图和BFS算法重复了测试。我将包含我所有的实验和我的解释。
本页其余部分故意留白,以便将相同步长并使用相同算法解决的拼图显示在一页上。
A* Man 算法在观察拼图尺寸效应方面没有给出非常有意义的结果。除了拼图尺寸为4时略高的数字外,我无法捕捉到任何数据趋势。对于 A* Man 来说,打乱程度越高的拼图似乎越难解决。即使对于尺寸为4的拼图,搜索空间更小,但与相同真实步长的较大拼图相比,A* 在获得结果方面付出了更多的努力。



为了验证我用 A* 获得的结果,我在 35 步蒙特卡罗运行中进行了相同的测试。A* 似乎没有受到拼图大小的很大影响。



然后我用BFS进行了相同的测试。我注意到拼图求解统计数据呈现线性-指数趋势。我得出的结论是,这是由于有效指数正在增加。我的意思是:当拼图大小为3且空白在角落时(4次),状态有两个后继;当空白在边缘时(4次),状态有3个后继;当空白在中间时,状态有4个后继(1次)。有效指数因子约为2.6。如果我们考虑其中一个后继导致循环,我的算法将不会存储它,有效指数因子降至1.6。但是,当拼图大小为4且空白在角落时(4次),状态有2个后继;当空白在边缘时(8次),状态有3个后继;当空白在中间时,状态有4个后继(4次)。有效指数因子为3。如果我们考虑其中一个后继导致循环,我的算法将不会存储它,有效指数因子降至2。因此,我可以得出结论,拼图尺寸的增加会增加有效指数因子,从而导致存储节点更多、扩展节点更多、解决时间更长,这对于更大的拼图是合理的。



6. 结论
我为滑动拼图问题实现了五种不同的算法。从这次带回家考试的实现中获得的经验非常有价值。现在我清楚地了解了这些算法在现实生活中的行为。
所有算法都能找到解决方案。此外,除了DFS之外,我的实现中所有算法都能找到最短(最优)解决方案。我的带有历史节点的拼图表示显著提高了算法的性能,并使DFS解决方案对该项目成为可能。
BFS的指数特性是微不足道的,它们在这个项目中得到了非常清晰的观察。
此外,DFS在搜索空间平均一半时找到解决方案的特点也非常明显。如果我们能提供更高真实步数的问题,DFS会比BFS更快地找到解决方案,因为BFS会搜索整个搜索空间,而DFS平均会搜索一半。
IDFS的重要性在课堂上对我来说不是很清楚,但我注意到IDFS以牺牲CPU功率和时间为代价,以最小的存储需求解决了问题。
正如预期,有信息搜索算法在整体解决方案性能上表现更好。拥有更好的启发式算法也明显提高了性能。
最终我得到的程序让我非常满意。这是我迄今为止编写过的最大段代码,其性能确实令人满意。
7. 致谢
我谨此感谢Orkun Ögücü在MATLAB数据绘图方面的支持,以及Serhat Varolgünes在C#多线程方面的支持。
8. 参考文献
[1] 人工智能:一种现代方法(第三版);Stuart Russell,Peter Norvig;Pearson 人工智能教育系列。
9. 附录
为了在MATLAB中更方便地绘图而获得的解码后的算法比较蒙特卡罗文本数据格式如下:“P”代表拼图;“000”、“001”代表拼图编号;“B”、“D”、“I”、“A”、“M”分别代表BFS、DFS、IDFS、A*Mis、A*Man。“ST”代表存储节点;“SS”代表解决方案步骤;“EN”扩展节点;“SN”存储节点。首字母后面的数字表示该值的具体数值。蒙特卡罗文本解码数据实际上是针对100个拼图的,但这里只给出了3个拼图的统计数据。
P 000 B ST 31 SS 5 EN 43 SN 30
P 000 D ST 39718 SS 129 EN 181323 SN 59444
P 000 I ST 0 SS 5 EN 110 SN 7
P 000 A ST 0 SS 5 EN 7 SN 9
P 000 M ST 0 SS 5 EN 6 SN 7
P 001 B ST 0 SS 5 EN 50 SN 42
P 001 D ST 36442 SS 213 EN 181248 SN 59439
P 001 I ST 0 SS 5 EN 92 SN 7
P 001 A ST 0 SS 5 EN 6 SN 7
P 001 M ST 0 SS 5 EN 6 SN 7
P 002 B ST 15 SS 5 EN 58 SN 41
P 002 D ST 0 SS 13 EN 14 SN 12
P 002 I ST 0 SS 5 EN 77 SN 6
P 002 A ST 0 SS 5 EN 6 SN 7
P 002 M ST 0 SS 5 EN 6 SN 7
P 003 B ST 0 SS 5 EN 49 SN 42
P 003 D ST 69888 SS 215 EN 181247 SN 59439
P 003 I ST 0 SS 5 EN 94 SN 7
P 003 A ST 0 SS 5 EN 6 SN 7
P 003 M ST 0 SS 5 EN 6 SN 7
尺寸比较数据只有一个算法。但它在最后也包含用“S”表示的尺寸信息。以下解码的蒙特卡罗数据属于尺寸为4的拼图。这里只显示了其中6个,但一个文件包含100个拼图的数据。
P 000 M ST 31 SS 31 EN 771 SN 801 S 4
P 001 M ST 0 SS 25 EN 274 SN 274 S 4
P 002 M ST 15 SS 25 EN 319 SN 323 S 4
P 003 M ST 1030 SS 29 EN 10124 SN 10256 S 4
P 004 M ST 172 SS 29 EN 2996 SN 3193 S 4
P 005 M ST 0 SS 25 EN 317 SN 321 S 4
所有用于 MATLAB 绘图的原始解码数据都可以在本项目提供的 MATLAB 文件夹中找到。
