65.9K
CodeProject 正在变化。 阅读更多。
Home

四元数数学和 3D 库（带 C# 和 GDI+）

YLS CS
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.91/5 (40投票s)

2009 年 6 月 1 日

CPOL

3分钟阅读

viewsIcon

122292

downloadIcon

7332

使用四元数旋转 3D 对象和使用 GDI+ 图形绘制 3D 对象。

引言

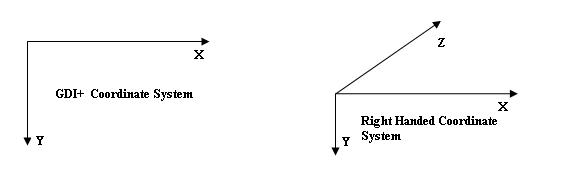
这个使用 C# 和 GDI+ 编写的 3D 库，允许您在三维空间中绘制图片，并旋转和/或移动 3D 对象。3D 库包括：Point3d.cs, Vector3d.cs, Shape3d.cs, Cuboid3d.cs, Quaternion.cs 和 Camera.cs。该库使用右手笛卡尔坐标系，并具有与 GDI+ 相同的 X、Y 坐标

关于程序

为了说明该库的工作原理，我编写了这个程序。当您运行此程序时，将加载一个彩色的立方体，并以像素为单位显示其中心和摄像机的位置。它们的旋转角度设置为零。此程序非常直观。您可以通过点击“加载图像”按钮在立方体的每个表面上放置图片。您也可以通过“重置”按钮重置此程序。 友情提示：由于旋转顺序不可交换，当所有旋转角度都返回到零时，立方体可能不在其初始状态。

关于代码

四元数

在数学中，四元数是一种非交换数系，它扩展了复数。它们为表示三维空间中对象的方向和旋转提供了一种方便的数学表示法。四元数有 4 个维度（每个四元数由 4 个标量数字组成），一个实数维度 w 和 3 个虚数维度 xi + yj + zk，可以描述旋转轴和角度。四元数经常用于 3D 引擎中，以快速旋转空间中的点。

定义四元数

q = w + xi + yj + zk = w + (x, y, z) = cos(a/2) + usin(a/2)

其中 u 是一个单位向量，a 是绕 u 轴旋转的角度。

设 v 是三维空间中的一个普通向量，被视为一个实坐标等于零 (w) 的四元数。那么四元数乘积

qvq-1

产生向量 v，该向量绕 u 轴旋转了角度 a。如果我们的视线指向 u 指向的方向，则旋转是顺时针的。此操作称为由 q 共轭。四元数乘法是旋转的组合，因为如果 p 和 q 是表示旋转的四元数，那么由 pq 旋转（共轭）是

	pqv(pq)-1 = pqvp-1p-1 = p(qvq-1)p-1

让我们看看 Quaternion.cs 的构造

    public struct Quaternion
    {
        public double X, Y, Z, W;
        
        public Quaternion(double w, double x, double y, double z)
        {
            W = w; X = x; Y = y; Z = z;
        }

        public Quaternion(double w, Vector3d v)
        {
            W = w; X = v.X; Y = v.Y; Z = v.Z;
        }

        public void FromAxisAngle(Vector3d axis, double angleRadian)
        {
            double m = axis.Magnitude;
            if (m > 0.0001)
            {
                double ca = Math.Cos(angleRadian / 2);
                double sa = Math.Sin(angleRadian / 2);
                X = axis.X / m * sa;
                Y = axis.Y / m * sa;
                Z = axis.Z / m * sa;
                W = ca;
            }
            else
            {
                W = 1; X = 0; Y = 0; Z = 0;
            }
        }
	... ...

四元数 q1 与 q2 的乘法是

(w1 + x1i + y1j + z1k)*(w2 + x2i + y2j + z2k)

和

i*j = k, j*k = i, k*i = j; i*i = -1, j*j = -1, k*k = -1

因此，我们可以根据上述信息轻松获得此代码

public static Quaternion operator *(Quaternion q1, Quaternion q2)
{
    double nw = q1.W * q2.W - q1.X * q2.X - q1.Y * q2.Y - q1.Z * q2.Z;
    double nx = q1.W * q2.X + q1.X * q2.W + q1.Y * q2.Z - q1.Z * q2.Y;
    double ny = q1.W * q2.Y + q1.Y * q2.W + q1.Z * q2.X - q1.X * q2.Z;
    double nz = q1.W * q2.Z + q1.Z * q2.W + q1.X * q2.Y - q1.Y * q2.X;
    return new Quaternion(nw, nx, ny, nz);
}

通过四元数旋转的代码如下

public void Rotate(Point3d pt)
{
    this.Normalise();
    Quaternion q1 = this.Copy();
    q1.Conjugate();
    
    Quaternion qNode = new Quaternion(0, pt.X, pt.Y, pt.Z);
    qNode = this * qNode * q1;
    pt.X = qNode.X;
    pt.Y = qNode.Y;
    pt.Z = qNode.Z;
}

public void Rotate(Point3d[] nodes)
{
    this.Normalise();
    Quaternion q1 = this.Copy();
    q1.Conjugate();
    for (int i = 0; i < nodes.Length; i++)
    {
        Quaternion qNode = new Quaternion(0, nodes[i].X, nodes[i].Y, nodes[i].Z);
        qNode = this * qNode * q1;
        nodes[i].X = qNode.X;
        nodes[i].Y = qNode.Y;
        nodes[i].Z = qNode.Z;
    }
}

相机

由于计算机显示器仅限于显示 2D 图像，我们必须使用投影将 3D 对象展平到 2D 平面上。Camera.cs 用于将 3D 点转换为平面上的 2D 点。Camera.cs 有三个属性

public class Camera
{
    Point3d loc = new Point3d(0, 0, 0);
    double _d = 500.0;
    Quaternion quan = new Quaternion(1, 0, 0, 0);

public Point3d Location
{
    set { loc = value; }
    get { return loc; }
}

public double FocalDistance
{
    set { _d = value; }
    get { return _d; }
}

public Quaternion Quaternion
{
    set { quan = value; }
    get { return quan; }
}
... ...

当摄像机移动时，其 Location 发生变化

public void MoveRight(double d)
{
    loc.X += d;
}

public void MoveLeft(double d)
{
    loc.X -= d;
}

public void MoveUp(double d)
{
    loc.Y -= d;
}

public void MoveDown(double d)
{
    loc.Y += d;
}

public void MoveIn(double d)
{
    loc.Z += d;
}

public void MoveOut(double d)
{
    loc.Z -= d;
}

当摄像机转动时，Quaternion 记录摄像机的旋转

public void Roll(int degree) // rotate around Z axis
{
    Quaternion q = new Quaternion();
    q.FromAxisAngle(new Vector3d(0, 0, 1), degree * Math.PI / 180.0);
    quan = q * quan;
}

public void Yaw(int degree)  // rotate around Y axis
{
    Quaternion q = new Quaternion();
    q.FromAxisAngle(new Vector3d(0, 1, 0), degree * Math.PI / 180.0);
    quan = q * quan;
}

public void Pitch(int degree) // rotate around X axis
{
    Quaternion q = new Quaternion();
    q.FromAxisAngle(new Vector3d(1, 0, 0), degree * Math.PI / 180.0);
    quan = q * quan;
}

public void TurnUp(int degree)
{
    Pitch(-degree);
}

public void TurnDown(int degree)
{
    Pitch(degree);
}

public void TurnLeft(int degree)
{
    Yaw(degree);
}

public void TurnRight(int degree)
{
    Yaw(-degree);
}

要将 3D 点投影到 2D，第一步是将原点平移到摄像机的 Location，并使用摄像机的 Quaternion 相对于摄像机的旋转来旋转 3D 对象。第二步是投影

public PointF[] GetProjection(Point3d[] pts)
{
    PointF[] pt2ds = new PointF[pts.Length];

    // transform to new coordinates system which origin is camera location
    Point3d[] pts1 = Point3d.Copy(pts);
    Point3d.Offset(pts1, -loc.X, -loc.Y, -loc.Z);

    // rotate
    quan.Rotate(pts1);

    //project
    for (int i = 0; i < pts.Length; i++)
    {
       if (pts1[i].Z > 0.1)
       {
           pt2ds[i] = new PointF((float)(loc.X + pts1[i].X * _d / pts1[i].Z),
           (float)(loc.Y + pts1[i].Y * _d / pts1[i].Z));
       }
       else
       {
           pt2ds[i] = new PointF(float.MaxValue, float.MaxValue);
       }
   }
   return pt2ds;
}
}

3D 对象和立方体

Shape3d.cs 是一个记录用于绘制形状的关键 3D 点并提供绘制 3D 形状的能力的原始基类

public class Shape3d
{
    protected Point3d[] pts = new Point3d[8];
    public Point3d[] Point3dArray
    {
        get { return pts; }
    }

    protected Point3d center = new Point3d(0, 0, 0);
    public Point3d Center
    {
        set
        {
            double dx = value.X - center.X;
            double dy = value.Y - center.Y;
            double dz = value.Z - center.Z;
            Point3d.Offset(pts, dx, dy, dz);
            center = value;
       }
       get { return center; }
    }

    protected Color lineColor = Color.Black;
    public Color LineColor
    {
        set { lineColor = value; }
        get { return lineColor; }
    }

    public void RotateAt(Point3d pt, Quaternion q)
    {
        // transform origin to pt
        Point3d[] copy = Point3d.Copy(pts);
        Point3d.Offset(copy,  - pt.X,  - pt.Y,  - pt.Z);
        
        // rotate
        q.Rotate(copy);
        q.Rotate(center);

        // transform to original origin
        Point3d.Offset(copy, pt.X, pt.Y, pt.Z);
        pts = copy;
    }
        
    public virtual void Draw(Graphics g,Camera cam)
    {
    }
}

现在可以构造任何 3D 对象。 这是一个简单的例子，Cuboid 派生自 Shape3d.cs

public Cuboid(double a, double b, double c)
{
     center = new Point3d(a / 2, b / 2, c / 2);
     pts[0] = new Point3d(0, 0, 0);
     pts[1] = new Point3d(a, 0, 0);
     pts[2] = new Point3d(a, b, 0);
     pts[3] = new Point3d(0, b, 0);
     pts[4] = new Point3d(0, 0, c);
     pts[5] = new Point3d(a, 0, c);
     pts[6] = new Point3d(a, b, c);
     pts[7] = new Point3d(0, b, c);
}

要在屏幕上绘制 3D 立方体，我们必须将其 3D 点传递给 Camera.cs 并获取用于绘制的 2D 点

public override void Draw(Graphics g, Camera cam)
{
     PointF[] pts2d = cam.GetProjection(pts);
     ... ...

您也可以填充立方体的表面；但是，您只能填充正面而不是背面。所以我们必须识别哪个是正面

if (YLScsDrawing.Geometry.Vector.IsClockwise(face[i][0], face[i][1], face[i][2]))
// the face can be seen by camera
{
   if (fillingFace) g.FillPolygon(new SolidBrush(faceColor[i]), face[i]);
   ... ...

为了增加趣味性，我通过 自由图像变换 将图片放置在正面上

if (drawingImage && bmp[i] != null)
{
    filters[i].FourCorners = face[i];
    g.DrawImage(filters[i].Bitmap, filters[i].ImageLocation);
}

谢谢

非常感谢您的阅读，祝您在使用我的 3D 库时玩得开心。

历史

  • 2009 年 6 月 1 日：初始帖子
© . All rights reserved.