宏伟项目3。与Simulink的兼容性
4.27/5 (11投票s)
导入 Simulink 文件。
- 下载航空+Simulink项目源代码 - 2.21 MB
- 下载航空+Simulink+OpenGL项目源代码 - 2.47 MB
- 下载航空+Simulink+WPF项目源代码 - 2.45 MB
- 下载机械聚合库源代码 - 932.54 KB
- 下载包含容器和3D形状的附加文件 - 333.84 KB
- 下载Simulink文件导入示例 - 8.2 KB
- 下载Simulink组件参数识别 - 14.96 KB
- 下载天线空间几何示例 - 2 KB
- 下载双通道跟踪系统示例 - 72.55 KB
- 下载双通道跟踪系统+虚拟现实示例 - 81.58 KB
其他有用资源
1. 引言
通用科学与工程框架应与任何第三方科学与工程软件兼容。与IronPython的兼容性已在“科学与工程通用框架 - 第12部分：宏伟项目”一文中讨论过。本文致力于与Simulink的兼容性。我尚未完全实现与Simulink的兼容性。相反，我找到了以下两个问题的答案
- *.mdl Simulink文件是否可以轻松通过框架导出；
- 导出这些文件提供了哪些优势。
我曾尝试开发一个能够导入一些Simulink文件的适配器，我发现兼容性问题相当容易解决。兼容性的优势将在本文及后续文章中讨论。目前我正在继续撰写“宏伟项目2。不可思议的机器”一文，我发现没有Simulink的不可思议的机器就不再不可思议。稍后我将Simulink示例添加到不可思议的机器中。由于“宏伟项目2。不可思议的机器”一文已经超载，我决定撰写新文章。两篇文章将同时撰写。本文致力于与Simulink的兼容性。我之前的文章将通过Simulink应用程序进行补充。
2. 背景
Simulink框图包含带有数学转换的模块。这些模块通过线条连接。线条的含义是信息流。该框架具有类型化的箭头。一种类型是信息流的消耗。框架具有其他类型的箭头，例如机械连接、相对几何位置、与物理场的相互作用等。因此，兼容性的主要思想是将信息流线转换为信息消耗箭头。
3. 展望
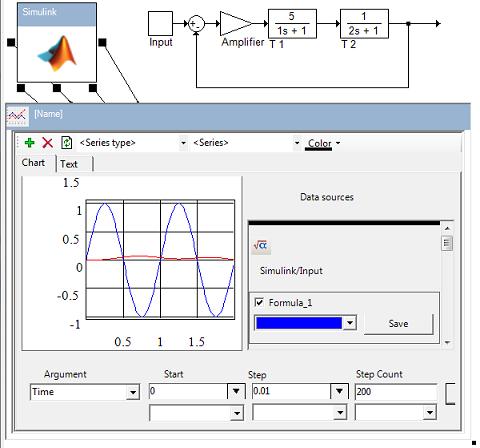
这个想法的展望将通过示例来考虑。假设我们有以下Simulink方案
此方案被翻译为以下框架方案
第二个方案中的箭头方向相反，并且第二个方案不包含反馈线。反馈通过另一种方式实现。让我们比较两个方案的元素。第一个方案中的输入元素由*.mdl文件的以下片段表示
| 块 { |
| 块类型 正弦 |
| 名称 “输入” |
| 幅度 “1” |
| 频率 “1” |
| } |
相应的框架元素具有以下属性
在这里，我们有明确的公式参数“幅度”和“频率”分别被替换为常数 a 和 f。下一个Simulinlk块已被替换为具有以下属性的块
负项 a 是“常数”。“常数”概念是约定俗成的。常数可以由不同的因素强制。我们跳过对 放大器 和 T 1 块的平凡描述。T 2 的属性如下所示
第一个窗口表示转换函数。第二个窗口表示该块的输出被发送到 Sum 的一个常数 a。因此，提供了反馈。
4. 用户界面
上面呈现的方案实际上是不可见的。我们有一个特殊的“Simulink”组件，具有以下属性
第一个选项卡允许我们编辑*.mdl文件文本。我们还可以下载*.mdl文件。第二个选项卡显示Simulink方案。第三个页面允许我们编辑公共组件的布局。结果，我们在桌面上得到以下组件
5. 实现
实现基于Simulink和框架组件之间的映射。框架组件存储在资源中。下图显示了与不同Simulink块对应的资源
增益（Gain）、正弦（Sin）、求和（Sum）资源对应于具有相同类型的Simulink块。编译过程将框架组件设置为Simulink块。
6. CodeDom编译
与Simulink的兼容性可以通过不同的方式实现。这里我们将考虑Simulink文件的CodeDom编译。CodeDom编译已在我的CodeProject文章和arxiv文章中讨论过。每个Simulink文件都可以转换为C#代码。让我们提供一个这种转换的示例。假设我们有以下Simulink方案
这个方案对应于以下代码
using System;
using System.Collections.Generic;
using System.Text;
using Simulink.CSharp.Library.Interfaces;
using Simulink.CSharp.Library;
namespace Calculation
{
public class Calculate : IStateCalculation
{
public void Update()
{
// First sum
arrow_3 = +arrow_1 - arrow_2;
// Mult
arrow_4 = (System_0_const_K) * arrow_3;
// Input of block 3
double block_3 = arrow_4 - ((1) * state[0]);
derivation[0] = block_3;
arrow_0 = +((5) * state[0]);
double block_4 = arrow_0 - ((2) * state[1]);
derivation[1] = block_4;
arrow_2 = +((1) * state[1]);
oldTime = time;
}
System.Double arrow_0;
System.Double arrow_1;
System.Double arrow_2;
System.Double arrow_3;
System.Double arrow_4;
public double[] State
{
get
{
return state;
}
}
public double[] Derivation
{
get
{
return derivation;
}
}
double[] state = new double[2];
double[] derivation = new double[2];
double time;
double oldTime;
public double Time
{
get
{
return time;
}
set
{
time = value;
}
}
double u = 0;
double System_0_const_K = 0;
public Dictionary<string, SetValue> Input
{
get
{
return input;
}
}
Dictionary<string, SetValue> input;
void SetBlock_0(object o)
{
arrow_1 = (System.Double)o;
}
public Dictionary<string, GetValue> Output
{
get
{
return output;
}
}
Dictionary<string, GetValue> output;
object GetBlock_0()
{
return arrow_2;
}
public Calculate()
{
input = new Dictionary<string, SetValue>();
input["Input"] = SetBlock_0;
output = new Dictionary<string, GetValue>();
output["Scope"] = GetBlock_0;
constants = new Dictionary<string, SetValue>();
constants["System_0_const_K"] = SetConst_0;
}
public void Reset()
{
arrow_0 = 0;
arrow_1 = 0;
arrow_2 = 0;
arrow_3 = 0;
arrow_4 = 0;
}
public Dictionary<string, SetValue> Constants
{
get
{
return constants;
}
}
Dictionary<string, SetValue> constants;
void SetConst_0(object o)
{
System_0_const_K = (double)o;
}
}
}
让我们评论一下这段代码。代码包含内在计算和外部访问成员。
6.1 内在计算
首先要注意的是，如果块通过线连接，那么这些块就有了共同的变量。例如，T 1 块的输出变量实际上是 T 2 块的输入变量。因此，箭头的标识符被用于这些变量。T 1 和 T 2 块的公共变量名为 arrow_0。内在块变量的名称包含“block_”前缀和块号。Update函数执行必要的计算。让我们评论一下其代码片段
// First sum
arrow_3 = +arrow_1 - arrow_2;
// Mult
arrow_4 = (System_0_const_K) * arrow_3;
第一个运算符对应方案的第一个求和元素。+ 和 - 号对应符号列表。此运算符计算arrow_3。arrow_3是求和元素的输出和增益的输入。第二个运算符对应增益元素。此运算符的结果是arrow_4。arrow_4是增益的输出和T 1转换函数的输入。因此我们翻译了方案的所有块。
6.2 外部访问
外部访问通过以下接口实现。
/// <summary>
/// State calulation
/// </summary>
public interface IStateCalculation
{
/// <summary>
/// Updates itself
/// </summary>
void Update();
/// <summary>
/// Resets itself
/// </summary>
void Reset();
/// <summary>
/// State
/// </summary>
double[] State
{
get;
}
/// <summary>
/// Derivation
/// </summary>
double[] Derivation
{
get;
}
/// <summary>
/// Input delegates
/// </summary>
Dictionary<string, SetValue> Input
{
get;
}
/// <summary>
/// Output delegates
/// </summary>
Dictionary<string, GetValue> Output
{
get;
}
/// <summary>
/// Constansts
/// </summary>
Dictionary<string, SetValue> Constants
{
get;
}
/// <summary>
/// Time variable
/// </summary>
double Time
{
get;
set;
}
}
/// <summary>
/// Sets value
/// </summary>
/// <param name="o">The value</param>
public delegate void SetValue(object o);
/// <summary>
/// Gets valuye
/// </summary>
/// <returns>The value</returns>
public delegate object GetValue();
GetValue (SetValue) 委托用于获取 (设置) 方案变量。Input 属性使我们能够向块输入值。以下示例提供了此类输入
IStateCalculation calc = null;
// Initialization of calc
SetValue sv = calc.Input["Input"];
double a = 5;
sv(a);
在此示例中，我们已将双精度值设置为输入变量（“Input”是变量名）。以下代码显示了读取“Scope”输出变量的值。
GetValue gv = calc.Output["Scope"];
object o = gv();
值得注意的是，Simulink方案通常是一个具有内部状态的系统。State (Derivation) 属性提供对状态向量（状态向量的导数）的访问。上述方案包含两个一阶变换函数。因此，该方案的状态向量维度等于2。我们有以下代码
public double[] State
{
get
{
return state;
}
}
public double[] Derivation
{
get
{
return derivation;
}
}
double[] state = new double[2];
double[] derivation = new double[2];
Time 属性使我们能够获取/设置当前时间。Constants 使我们能够设置常量的值。Reset 方法将系统设置为其初始状态。
7. 应用
Simulink的仿真作为独立功能并不有趣。它作为集成到框架中才有趣。这种集成使我们能够使用力学、场论、虚拟现实和其他有用的功能。
7.1 系统参数识别
让我们再次考虑以下Simulink方案
图标表示使用Simulink包装器和C#编译。Input 组件为Simulink 组件提供输入。Input 的属性如下所示
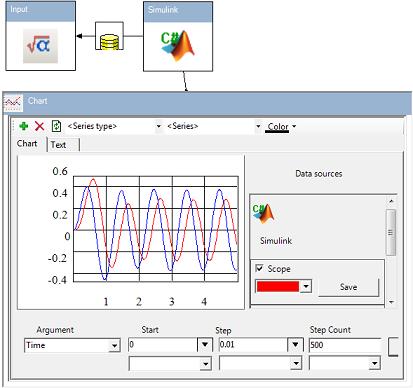
这些属性具有以下含义。Simulink方案的 Input 参数等于 Input 组件的 Formula_1。Simulink方案的 K 常数的值等于1.9（K 是增益系数）。假设我们记录了另一个 K 值下的信号，并且我们想定义这个值。两个信号如下图所示
红色曲线对应于 K = 1.9，绿色曲线对应于我们想要定义的另一个 K 值。我们将使用以下方案实现我们的目的
让我们解释一下这个方案中各个组件的含义。Input 和 Simulink 组件的含义已经解释过了。Series 组件包含了导入的带有另一个 K 值的信号。Accumulator 组件累积了 Simulink 组件的输出。Accumulator 的属性如下图所示
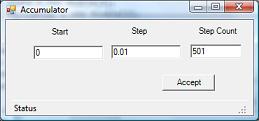
该组件累积信号。累积步长等于0.01。步数等于501。Result 组件具有以下属性
此组件计算 f(x)。 f 是 Accumulator 的输出函数， x 是 Series 组件的x坐标数组。因此 f(x) 包含 Simulink 组件输出信号的y坐标。Processor 属性如下所示
这些属性具有以下含义。右侧和中间部分表示我们希望通过 Result 的 Formula_1 来近似 Series 的 y 坐标。左侧部分表示可识别参数是 Simulink 组件的 K 系数。粗略地说，算法正在寻找一个 K 值，使得 Simulink 的输出信号与导入的信号（Series）匹配。经过此识别过程后，我们得到了新的 K 值（见下文）。
7.2 跨学科示例。雷达双通道跟踪系统
雷达双通道跟踪系统已在我的文章“科学与工程通用框架 - 第3部分：控制系统。信号处理”中讨论过。此示例更高级，展示了该框架的跨学科特性。它包括以下科学与工程分支
- 空间几何学；
- 场论；
- 高级力学；
- 控制理论；
- 虚拟现实。
7.2.1 问题展望
问题概述图如下
雷达天线具有双通道跟踪系统，包括方位角和俯仰角通道。这种现象的空间几何结构如下所示
输入数据是从信号反射获得的。控制系统作用于雷达。因此，雷达跟踪可见线。让我们考虑一下这个问题的理论问题。
7.2.2 理论问题
7.2.2.1 方向定义的相位法
相位定义方向的方法可以通过以下几何任务来解释。假设我们有一个等边空间三角形 ABC。
7.2.2.2 高级力学
一般来说，雷达天线不能被认为是机械绝对刚体。因此，这里将考虑天线的弹性振荡。该框架包含一个聚合设计器，对弹性机械模拟提供了良好的支持。这个聚合设计器在我的前一篇文章中有所描述。在这里我再次提及。为什么是聚合设计器？事实上，机械方程很久以前就已为人所知。但是开发用于模拟复杂机械对象的软件并不是一项容易的任务。聚合设计器使这项任务变得容易得多。让我们以航天器模块的模型为例，考虑航天器的机械模型。典型的航天器模块示意图如下所示
此模块具有自己的坐标系OXYZ。它还有连接点。我们可以将其他模块连接到此模块。模块的行为由以下运动学参数定义
- 半径向量 r；
- 速度 V；
- 方向四元数 Q；
- 角速度
。
但模块通常不是刚性的。这些参数也不是模块的参数。这些参数更像是模块某个点的参数。在本文中，我们假设这些参数是OXYX坐标系原点的参数。由于模块不是刚性的，它具有额外的自由度。这些自由度可以解释为广义坐标 qi (i = 1,...,n)。模块的瞬时状态由以下参数定义
我将它们称为状态变量。参数
将被称为加速度。力学方程通过状态参数定义加速度。连接附近的加速度可以通过以下方式定义
其中 i 是连接的编号。其他变量是取决于状态变量的矩阵。让我们连接两个模块
两个模块在连接处具有相同的加速度。第一个模块通过力 F12 和机械力矩 M12 作用于第二个模块。类似地，第二个模块通过力 M21 和机械力矩 F21 作用于第一个模块。以下方程
F12 = -F21；
M12 = -F21；
是众所周知的。模块的机械方程可以表示为以下形式
在这些表达式中，加速度是独立变量。Fi (Mi) 是第 i 个连接模块的力（机械力矩）。其他向量和矩阵参数取决于状态变量。添加以下明显表达式
得到关于加速度的线性方程组。该系统使我们能够找到所有加速度。因此我们有了机械方程。值得注意的是，该系统是冗余的。如果第一个（第二个）模块的自由度数为 n1(n2)，则系统具有 n1 + n2 个自由度。然而，聚合体具有 n1 + n2 - 6 个自由度。该框架可以避免这种冗余。但我不会在本文中描述它。模块类型有很多。所有这些都以编程方式实现以下接口
/// <summary>
/// Aggregable Mechanical Object
/// </summary>
public interface IAggregableMechanicalObject
{
/// <summary>
/// Number of degrees of freedom
/// </summary>
int Dimension
{
get;
}
/// <summary>
/// Number of connections
/// </summary>
int NumberOfConnections
{
get;
}
/// <summary>
/// State of object
/// </summary>
double[] State
{
get;
}
/// <summary>
/// Internal acceleration
/// </summary>
double[] InternalAcceleration
{
get;
}
/// <summary>
/// State of connection
/// x[0] - position, x[1] - quaternion,
/// x[2] - linear velocity, x[3] - angular velocity
/// </summary>
/// <param name="numOfConnection">Number of connection</param>
/// <returns>State of connection</returns>
double[] this[int numOfConnection]
{
get;
set;
}
/// <summary>
/// Calculates transformation matrix from genrealized coordinates to
/// acceleration of connection
/// </summary>
/// <param name="numOfConnection">Number of connection</param>
/// <returns>The transformation matrix</returns>
double[,] GetAccelerationMatrix(int numOfConnection);
/// <summary>
/// Gets matrix of forces
/// </summary>
/// <param name="numOfConnection">Number of connection</param>
/// <returns>The matrix of forces</returns>
double[,] GetForcesMatrix(int numOfConnection);
/// <summary>
/// Gets internal acceleration
/// </summary>
/// <param name="numOfConnection">Number of connection</param>
/// <returns>Internal accceleration</returns>
double[] GetInternalAcceleration(int numOfConnection);
/// <summary>
/// Gets connection force
/// <summary>
/// <param name="numOfConnection">Number of connection</param>
/// <returns>Connection force</returns>
double[] GetConnectionForce(int numOfConnection);
/// <summary>
/// Children objects
/// </summary>
Dictionary<IAggregableMechanicalObject, int[]> Children
{
get;
}
/// <summary>
/// The is constant sign
/// </summary>
bool IsConstant
{
get;
}
/// <summary>
/// Parent object
/// </summary>
IAggregableMechanicalObject Parent
{
get;
set;
}
}
下面我将考虑模块示例。这里我描述这个接口。此接口成员的含义在下表中列出
| 数字 | 成员 | 评论（含义） |
| 1 | 维度 | 微分方程组的维数 |
| 2 | 连接数 | 与其他聚合体的连接数 |
| 3 | 状态 | 状态向量（包含微分方程的独立变量） |
| 4 | 内部加速度 | 广义坐标的加速度 |
| 5 | this[int numOfConnection] | 连接状态 |
| 6 | GetAccelerationMatrix | 连接的加速度矩阵 |
| 7 | GetForcesMatrix | 连接的力矩阵 |
| 8 | GetConnectionForce | 连接力矩 |
| 9 | 子级 | 子聚合体 |
| 10 | IsConstant | 是常量标志 |
| 11 | Parent | 父对象 |
IsConstant 标志。下面的聚合库包含一组基本的机械对象。
第一个库对象代表刚体力学。刚体的方程是众所周知的，我在此不赘述。刚体具有可变数量的连接。其属性编辑器如下所示
连接的数量、位置和方向都可以改变。弹性悬臂梁是一个具有无限自由度的机械系统。通常，该对象的数学模型包含有限自由度，并具有有限组有价值的谐波振荡。每个谐波振荡都可以通过以下二阶常微分方程组来描述
弹性体的属性编辑器如下所示
该编辑器使我们能够更改谐波数及其数值属性。此类对象用于模拟天线力学。
7.2.2.3 声明式几何方法
计算中的直接或命令式方法使用物理现象的显式“表达式”，例如“计算以下表达式”。这种方法包含命令式方法的所有缺点。这里我们将使用声明式方法，它具有以下优点
- 简洁；
- 与其他现象良好的互操作性。
让我们提供声明式描述。存在一个移动物体，移动物体的物理场自然地与移动物体几何相关联。存在一个弹性天线，它与物理场相互作用。相互作用取决于移动物体和天线的相对位置。然而，声明式方法使我们能够隐式地考虑这种依赖关系。工程师有很多问题，除了对几何位置的几何依赖性的显式描述。这项任务也用于虚拟现实。虚拟现实也隐式地考虑了几何位置。
7.2.2.4 控制理论
跟踪系统的典型控制方案是PID控制。微分提供稳定性。积分提供无差性。Simulink用于模拟PID控制器。Simulink中实现了许多控制律。现在这些控制律可以导出到框架中。
7.2.3 实现
7.2.3.1 移动物体
移动物体由以下图表实现
运动方程包含显式运动学公式
运动帧是移动参考帧。它通过以下方式使用运动方程的公式
上图具有以下含义。运动帧坐标的时间依赖性 X(t)、Y(t)、Z(t) 分别由 运动方程 对象的 Formula_1、Formula_2、Formula_3 表示。方向四元数的 Q0(t)、Q1(t)、Q2(t)、Q3(t) 分量的时间依赖性由 Formula_4、Formula_5、Formula_6、Formula_7 表示。稍后，运动帧的几何位置将隐式使用。
7.2.3.2 移动物体的物理场
物理场的仿真如下图所示
主要对象是 Field。GL 箭头表示该场与 Motion frame 几何关联。因此箭头 GL 纯粹是声明性的。并且 Motion frame 的位置是隐式考虑的。Field Math 对象包含相位场的显式公式
这里 x, y, z 是几何点的相对坐标，a 是辐射场的波数。对象 Field 具有以下属性
这些属性具有以下含义。相对坐标 x, y, z 分别与 Field Math 对象的变量 x, y, z 关联。Field 的值对应于 Field Math 对象的 Formula_3。请注意，这里也使用了抽象（声明式）方法。我们没有明确指出 x, y, z 坐标。
7.2.3.3 接收机模型
我们将使用7.2.2.1节中描述的三点近似模型。该模型如下所示
该模型包含三个虚拟传感器 S 1、S 2 和 S 3。传感器分别安装在参考系 1、2 和 3 上。这些框架的位置是相对于参考系 Base 考虑的。稍后，Base 将安装在天线的参考系上（作为机械物体）。1、2 和 3 相对于 Base 移动。这种相对运动是由天线（作为机械物体）的弹性振荡引起的。Coordinates 对象包含此运动的公式。稍后，Coordinates 对象将与弹性振荡的表达式链接。上图不适合后续使用，因为它包含许多我们将来不会编辑的对象。封装此图将很有用。为此我们有一个容器设计器。下图显示了接收机的封装
勾选的框对应以下对象
- 坐标；
- 基座；
- S 1；
- S 2；
- S 3。
Coordinates 属性将链接到弹性振荡值。Base 帧将链接到天线的帧（作为机械对象）。S 1、S 2、S 3 将用于计算反射信号。封装对象如下所示
7.2.3.4 与场的相互作用
与场的相互作用模型如下所示
为了实现交互，我们简单地将虚拟传感器 S 1、S 2、S 3 通过“传感器-场交互” 
箭头连接到 Field。传感器包含在封装的 Antenna 对象中。因此，Antenna 附近三个小黑方块对应于传感器。尽管我们只连接了方块，但许多操作都是隐式执行的。首先，考虑了传感器相对于场的相对位置。其次，我们注意到在 Field 中我们没有明确指出相对坐标 x、y、z。这里我们为三个对象 S 1、S 2、S 3 使用这些（抽象）坐标（每个对象的自由坐标）。此操作也是隐式执行的。
7.2.3.5 天线力学模型
天线的机械模型是具有6个弹性谐波的弹性体。天线的属性如下所示
天线受到控制系统的机械力矩作用。这个力矩将在下面讨论。
7.2.3.6 力学与接收机属性的相互作用
我们已经注意到，常规点的位置取决于弹性振荡。这种依赖关系可以通过以下方式表达
其中 
是任意常规点的任意坐标的位移，qi 是广义坐标，ki 是系数。系数集（作为一个整体）取决于条件点数和坐标名称（x,y,z）。这种依赖关系的实现如下图所示
让我们解释一下组件的含义。天线力学 的一个输出参数是广义坐标的向量 q。弹性位移 对象使用此输出向量。下图显示了 弹性位移 的属性
图片右半部分表示 x 变量是广义坐标 q 向量的别名。ax 表达式是点积。a 变量是具有以下属性的常数向量
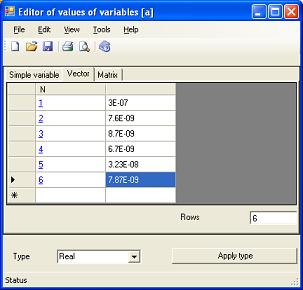
弹性位移 包含 9 个标量积。9 这个数字的原因是：我们有三个点，每个点有 3 个坐标。弹性位移 对 位移 对象有反馈
此反馈会改变 Shifts 对象的“常数”。Shifts 对象计算常数位移与弹性振荡引起的位移之和。Shifts 由封装在 Antenna 对象中的 Coordinates 对象使用。我们已经描述过（参见 7.2.3.3），Coordinates 对象包含常规点的坐标。
7.2.3.7 跟踪算法
我们的系统有两个通道
- 仰角
- 方位角
天线有三个相位信号。我们想从三个相位信号中制作两个偏差信号。信号的几何结构如下图所示
这里 A、B 和 C 是常规点，P 是观测物体的位置。在标称情况下，区间 AP、BP 和 CP 的长度相等。然而，如果 P 以 L 线绕 x 轴旋转的方式移动，则 |PA| 不应等于 |PB|。因此，|PA| - |PB| 的差值可以视为可见线绕 y 轴的偏差（方位角偏差）。同样清楚的是，由绕 y 轴旋转引起的偏差与 (|PA|+|PB|)/2 - |PC| 成比例。我们没有长度 PA|、|PB| 和 |PC|。但我们有相位差，可以通过它们来估计偏差。完整的控制逻辑如下图所示
Delta组件通过以下方式计算偏差
右侧窗格表示 x、y 和 z 变量分别对应于 S 1、S 2、S 3 传感器的输出。Formula_1 和 Formula_2 分别对应于方位角和俯仰角偏差。偏差由 PID 控制器 Channel 1 和 Channel 2 对象使用，这些对象作为 Simulink 对象的代理实现。PID_Controller.mdl 文件已下载并用于此情况。这些对象具有以下属性
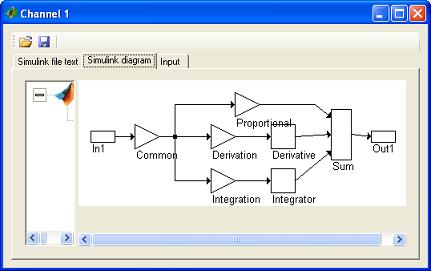
第一张图片表示*.mdl文件的逻辑。第二张图片表示常数和输入变量。这里的输入变量是Delta对象的Formula 1或方位角偏差。Channel 2的属性与Channel 2的属性非常相似。这些对象的输出用作天线的控制机械力矩。这一事实反映在天线力学的以下属性中
这张图片具有以下含义。机械力矩 Mx、My 分别等于 Channel 1 和 Channel 2 的输出。完整的模拟图如下所示
典型的过渡过程如下图所示
第一个图表包含偏差，第二个图表包含天线角速度的分量。此示例需要附加文件。
7.2.3.8 虚拟现实
我们已经考虑了双通道跟踪系统的物理现象。现在，这些物理知识将用于虚拟现实。我们希望通过安装在天线上的虚拟摄像机来呈现移动物体的视图。首先，我们提供摄像机的正确方向。摄像机的可见轴应与天线的可见轴共线。然而，天线的可见轴并不总是与天线的任何机械轴规范地重合。将引入附加框架以提供摄像机的正确方向。此框架如下图所示
该框架名为 Following Rotation。稍后，虚拟摄像机将安装在此框架上。由于虚拟现实不需要相对位置和方向，我们可以封装物理。结果，我们得到以下对象。
此对象有三个公共对象
- 基础参考系；
- 移动物体的参考系；
- 安装在天线上的摄像机的参考系。
现在我们将构建以下场景
此图包含以下对象
| 对象名称 | 注释 |
| 随动运动 | 物理现象的封装物理 |
| 平面 | 运输机的3D图形模型 |
| 跟踪相机 | 安装在天线上的虚拟摄像机 |
| 前进 | 附加虚拟摄像机的参考帧 |
| 侧面 | -"- |
| 低功耗 | -"- |
| 前置摄像头 | 附加虚拟摄像机 |
| 侧面摄像头 | -"- |
| 低位摄像头 | -"- |
此示例需要附加文件和框架的“航空 + Simulink + OpenGL”版本。
要尝试此示例，您需要设置虚拟现实的参数（开始时间、开始步长、步长、步数和暂停），如下图所示
然后应点击“开始” 
按钮。这些参数更合适的值如下表所示
| 参数 | 值 |
| 开始时间 | 0 |
| 起始步骤 | 0.02 |
| 步数 | 400 |
| 暂停 | 0 |
7.2.4 WPF 3D可视化版本
该框架成立于2002年。第一个虚拟现实框架基于OpenGL。在撰写本文期间，WPF可视化被开发出来。因此，为本文提供WPF可视化源代码是合理的。您可以下载它。您还可以下载上述情况。
WPF 3D性能大幅超越OpenGL。因此我们需要设置动画的以下参数
| 参数 | 值 |
| 开始时间 | 0 |
| 起始步骤 | 0.0002 |
| 步数 | 40000 |
| 暂停 | 0 |
7.2.5 结论
这个例子展示了声明式方法的优点。如果我们声明了（相对）几何位置，那么我们就不必关心许多其他细节。物理场的作用会自动考虑位置和方向。控制信号取决于物体的相对方向和位置。反之，相对方向和位置取决于控制信号。之后，运动模拟用于虚拟现实。虚拟现实和物理现象模拟都使用参考帧。虚拟现实模拟成为在物理现象模拟提供的参考帧上安装虚拟摄像机和3D模型。
7.3 状态流。自动变速箱控制
Simulink支持状态流。现在状态流在IT领域的重要性显而易见。此外，某些编程语言（例如C#）也支持状态流。我认为与Simulink状态流兼容的最佳方式是使用Windows Workflow Foundation。让我们考虑以下示例。自动变速箱控制是典型的流程问题。自动变速箱系统的完整Simulink图表如下所示
此方案包含一个子方案目录。Simulink的框架包装器通过以下方式表示此目录
左侧窗格表示目录结构。右侧窗格表示子方案。自动变速箱控制的逻辑在此描述。此逻辑包含状态机，这些状态机如下图所示
很明显，以下Windows Workflow Foundation图表实际上表示相同的状态机。
因此，Simulink状态机与框架状态机兼容的自然方式是将Simulink状态流转换为Windows Workflow Foundation。
等待
关注点
与Simulink的兼容性将提供许多前景。许多工程开发可以被导入。
历史
我决定在2008年11月提供兼容性。但我并不知道实现这个想法的好方法。2009年6月，我找到了一个实现这个想法的好方法。在10天内，我开发了第一个版本。历史尚未结束。这篇文章更像是一个公告。许多*.mdl文件尚无法导入。这篇文章和代码将得到扩展。
<input type="hidden" id="gwProxy" /><input type="hidden" id="jsProxy" önclick="jsCall();" />