向折线添加一个点
4.84/5 (7投票s)
在折线中插入一个新点

引言
在许多情况下,找到离线最近的点并在线上添加一个点(如下图中的虚线所示)是很有趣的。存在一个计算点到直线距离的公式,例如 MathWorld 上的这个。但是,该公式的问题在于它只计算两个点确定的无限延伸直线与一个点之间的距离。这意味着它不受由相邻线段形成的有限线段的限制。
标准的方法是使用线段的 Voronoi 图来确定点应该添加到哪条线上。这种方法非常精确,但从头开始实现并不容易,即使你已经有了普通点 Voronoi 图的代码。当然也有现成的库,但需要付费使用,并且在大多数情况下(我打算使用它的情况)来说,它们过于复杂而不可行。下面展示了一个 Voronoi 图的例子,其中所有蓝线(大部分)显示的是到两条线距离相等的边界。
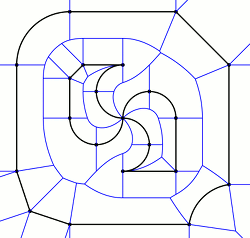
我将演示的算法会在点位于蓝线边界内时添加该点,也就是说,它会将点添加到最近的线上。
背景
有几种潜在的方法可以解决这个问题,一种方法是构建一个具有线的 Voronoi 图,如此处所述,该图会自动设置点应该添加到线的边界。但除非你有一个现成的预编程代码,否则这是一项艰巨的任务。因此,我想要一个简单的解决方案。
一种解决方案是设计一种算法,该算法考虑曲线的弯曲度,并且如果点不在边界内,则不会将其添加到线段。边界显示在下图中,用红色向量表示:

线的 Voronoi 图会自动完成此操作。
使用的函数
首先,我需要描述一些使代码正常工作的简单函数。这些是几个问题中使用的基本几何函数,无论手头的具体问题是什么,它们都很有用。
首先,我们需要找到两条连接线之间的夹角,这可以通过“余弦定理”来完成。下面的代码以度为单位返回角度。
''' <summary>
''' Calculate the angle in degrees between point 1 and 3 at point 2
''' </summary>
''' <param name="Point1"></param>
''' <param name="Point2"></param>
''' <param name="Point3"></param>
''' <returns></returns>
''' <remarks></remarks>
Public Function Angle(ByVal Point1 As Point, ByVal Point2 As Point, _
ByVal Point3 As Point) As Double
Dim result As Double
Dim a, b, c As Double
c = DistanceBetweenPoints(Point1, Point3)
b = DistanceBetweenPoints(Point1, Point2)
a = DistanceBetweenPoints(Point2, Point3)
result = Math.Acos((a ^ 2 + b ^ 2 - c ^ 2) / (2 * b * a)) * 180 / Math.PI
Return result
End Function
下一个代码片段是来自MathWorld的代码,它计算点到由两个点确定的无限直线之间的距离:
''' <summary>
''' Returns the distance from a point to a line
''' </summary>
''' <param name="LinePoint1"></param>
''' <param name="LinePoint2"></param>
''' <param name="TestPoint"></param>
''' <returns></returns>
''' <remarks></remarks>
Public Function DistanceFromLine(ByVal LinePoint1 As Point, _
ByVal LinePoint2 As Point, TestPoint As Point) As Double
Dim d As Double
d = Math.Abs((LinePoint2.X - LinePoint1.X) * (LinePoint1.Y - TestPoint.Y) - _
(LinePoint1.X - TestPoint.X) * (LinePoint2.Y - LinePoint1.Y))
d = d / Math.Sqrt((LinePoint2.X - LinePoint1.X) ^ 2 + (LinePoint2.Y - LinePoint1.Y) ^ 2)
Return d
End Function
下一个问题是确定点相对于直线的位置,这可以通过叉乘找到直线的法向量来完成,详细解释在此。代码如下:
''' <summary>
''' Finds which side of a line the point is
''' </summary>
''' <param name="PointToBeEvaluated">Evaluation point</param>
''' <param name="StartPointOnLine">Startpoint of line</param>
''' <param name="EndPointOnLine">Endpoint on line</param>
''' <returns>-1 for a point to the right, 0 for a point on the line, +1 for a point to the left</returns>
''' <remarks></remarks>
Private Function WhichSide(ByVal PointToBeEvaluated As Point, ByVal StartPointOnLine _
As Point, ByVal EndPointOnLine As Point) As Integer
Dim ReturnvalueEquation As Double
ReturnvalueEquation = ((PointToBeEvaluated.Y - StartPointOnLine.Y) _
* (EndPointOnLine.X - StartPointOnLine.X)) - ((EndPointOnLine.Y - StartPointOnLine.Y) _
* (PointToBeEvaluated.X - StartPointOnLine.X))
If ReturnvalueEquation > 0 Then
Return -1
ElseIf ReturnvalueEquation = 0 Then
Return 0
Else
Return 1
End If
End Function
还需要一个计算单直线法向量的函数。这对于所有点都是必需的。
''' <summary>
''' Calculates the Normal vector at point 1
''' </summary>
''' <param name="Point1"></param>
''' <param name="point2"></param>
''' <returns></returns>
''' <remarks></remarks>
Public Function Normal2D(ByVal Point1 As Point, ByVal point2 As Point) As Point
Dim p As New Point
Dim theta As Double
theta = Math.PI / 2
p.X = Math.Cos(theta) * (point2.X - Point1.X) - Math.Sin(theta) * (point2.Y - Point1.Y) + Point1.X
p.Y = Math.Sin(theta) * (point2.X - Point1.X) + Math.Cos(theta) * (point2.Y - Point1.Y) + Point1.Y
Return p
End Function
现在可以使用这些简单的函数构建代码。我们将首先计算所有边界线(在第一张图中显示为红色),并在每个点添加一个我们可以绘制它的向量。下面的代码利用了上述函数
Public Function CalculateAllAngles(ByVal OriginalPointCollection As PointCollection) As List(Of VectorLine)
Dim result As New List(Of VectorLine)
For i As Integer = 0 To OriginalPointCollection.Count - 1
Dim NewVectorLine As New VectorLine
If i = 0 Then
NewVectorLine.Point2 = Normal2D(OriginalPointCollection(i), _
OriginalPointCollection(i + 1))
NewVectorLine.Point1 = OriginalPointCollection(i)
result.Add(NewVectorLine)
ElseIf i = OriginalPointCollection.Count - 1 Then
NewVectorLine.Point2 = Normal2D(OriginalPointCollection(i), _
OriginalPointCollection(i - 1), 3 * Math.PI / 2)
NewVectorLine.Point1 = OriginalPointCollection(i)
result.Add(NewVectorLine)
Else
NewVectorLine.Point1 = OriginalPointCollection(i)
Dim angl As Double = Angles(OriginalPointCollection(i - 1), _
OriginalPointCollection(i), OriginalPointCollection(i + 1))
Dim PreviousAngle, NextAngle As Integer
PreviousAngle = WhichSide(result(i - 1).Point2, _
OriginalPointCollection(i - 1), OriginalPointCollection(i))
NextAngle = WhichSide(OriginalPointCollection(i + 1), _
OriginalPointCollection(i - 1), OriginalPointCollection(i))
If PreviousAngle = NextAngle Then
NewVectorLine.Point2 = Normal2D(OriginalPointCollection(i), _
OriginalPointCollection(i + 1), angl / 2)
Else
NewVectorLine.Point2 = Normal2D(OriginalPointCollection(i), _
OriginalPointCollection(i + 1), (2 * Math.PI - angl) / 2)
End If
result.Add(NewVectorLine)
End If
Next
Return result
End Function
Public Class VectorLine
Public Point1 As New Point
Public Point2 As New Point
End Class
代码相当简单,可以分解为简单的步骤
第一个和最后一个点分别使用第一个和最后一个线段,分别以 90 度和 270 度倾斜来计算。
其他点的角度通过使用余弦定理找到。向量使用最短角度计算,如果计算出的向量点与第一个计算出的向量点在同一侧,则将其存储。如果它在相反的一侧,则通过从整个圆中减去该角度来重新计算向量。
计算出的向量线随后从函数返回。
完整的算法
进行计算的代码如下
''' <summary>
''' Insert a new point to the line
''' </summary>
''' <param name="OriginalPointColletion"></param>
''' <param name="NewPoint"></param>
''' <returns></returns>
''' <remarks></remarks>
Public Function InsertPoint(ByVal OriginalPointColletion As PointCollection, _
ByVal NewPoint As Point) As PointCollection
Dim result As New PointCollection
result = OriginalPointColletion.Clone
Dim min_distance As Double = Double.MaxValue
'For Each p As Point In result
' min_distance += DistanceBetweenPoints(NewPoint, p)
'Next
Dim temp_distance As Double
Dim index As Integer
Dim VectorLinesCalc As New List(Of VectorLine)
VectorLinesCalc = CalculateAllAngles(OriginalPointColletion)
For i As Integer = 0 To OriginalPointColletion.Count - 2
temp_distance = DistanceFromLine2(NewPoint, VectorLinesCalc(i), VectorLinesCalc(i + 1))
If temp_distance < min_distance Then
min_distance = temp_distance
index = i + 1
End If
Next
If DistanceBetweenPoints(OriginalPointColletion(0), NewPoint) < min_distance Then
min_distance = DistanceBetweenPoints(OriginalPointColletion(0), NewPoint)
index = 0
End If
If DistanceBetweenPoints(OriginalPointColletion(OriginalPointColletion.Count - 1), NewPoint) < min_distance Then
index = -1
min_distance = DistanceBetweenPoints(OriginalPointColletion(OriginalPointColletion.Count - 1), NewPoint)
End If
If Not index = -1 Then
result.Insert(index, NewPoint)
Else
result.Add(NewPoint)
End If
Return result
End Function
我只需计算每条线到你尝试交叉的新点的距离。但是,如果该点不在边界内,则返回距离 Double.MaxValue。这将保证距离最短的点自然最接近相关线。
我判断点是否超出边界的方法是检查两个边界向量是否不相等,因为我们正在评估距离的计算,所以这会很好地工作。
历史
由于一个 bug,代码得到了大幅升级。此外,UI 也得到了升级,主要是为了 bug 检查代码,但它也应该能帮助你更详细地理解算法。代码以 C# 和 VB 提供,主函数也被封装在一个单独的类/模块中,因此可以轻松地将其实现到其他地方。
