圆形迷宫

• 下载 exec.zip - 9.4 KB
• 下载源代码 - 22.5 KB

引言

存在不少迷宫生成算法，但随机性在其中大多数扮演着核心角色。尽管这些算法可以创建具有挑战性的迷宫，但它们无法轻易保证生成迷宫的某个特定属性。例如：限制恰好有四个死胡同。因此，纯粹的随机性可能不是最佳选择。

在本文中，我将重点介绍圆形迷宫（见图 1），因为它们具有一种深度感；玩家从迷宫最外圈开始，一层一层地向内前进，直到通过到达最内圈来解决迷宫。在本文中，我将介绍一种方法，它将允许您构建一个具有所需属性的圆形迷宫。

背景  

让我们先从一些术语开始

 

• 蓝色 - 门
• 绿色 - 障碍
• 红色 - 死胡同
• 数字 - 环级别

核心概念

创建迷宫的整个过程严重依赖于树结构。

我们的树与迷宫之间的关系如下：

• 树的每个级别 (i) 对应于迷宫中的一个圆 (i)，因此迷宫中的圆数等于树的高度。
• 树的节点代表某个环中的一个门。例如，树的根是进入迷宫的入口：最外圈的一个开口。
• 连接级别 (i) 的节点 A 和级别 (i+1) 的节点 B 的边将确保从环 (i) 到内环 (i+1) 的直接路径。
• 父节点 P 拥有两个子节点 A 和 B（或更多）将导致每个子节点之间存在障碍；这是因为从 A 的子树中的节点到 B 的子树中的任何节点的唯一方法是访问 P。
• 迷宫的解是从树的根到最低级别的一个节点（深度等于树高度的节点）的一条路径。

您可以看到，一棵树完全定义了迷宫。例如，如果我们想构建一个具有六个环、八个死胡同和两条不同解路径的迷宫，我们可能会创建如下树：

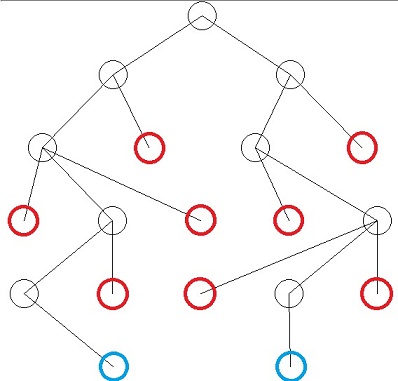
红色节点：死胡同。

蓝色节点：通往最内圈的入口（解的最后一步）

好的，现在主要思想已经到位（树 -> 迷宫），我们如何根据给定的树实际绘制迷宫？我们必须弄清楚以下几点：

• 对于每个门，我们需要确定它在环上的位置。
• 对于级别 (i) 的每个节点，我们需要弄清楚它的段尺寸，即：它界定了其内圆 (i+1) 的哪个部分（参见图 1）。

经验法则

门的位置和障碍位置（由角度表示）的计算是从最内圈向外进行的，遵循一个经验法则：在尝试确定门的角度时，它的左侧和右侧障碍已由前一个步骤确定。

最深级别的节点经过特殊处理，因为它们没有障碍。对于这些节点，我们将首先将环分成 N 个段，其中 N 是树最深级别上的节点数。然后，我们通过在每个节点在其段的边界内选择一个随机角度来确定它们的位置。

例如：假设我们有三个节点：A、B 和 C 在最深级别，父节点 Pa 通向 A，Pb 通向 B，Pc 通向 C。将 360 除以 3 会创建三个段，每个段的范围为 120 度。一种可能性是将 A 定位在 85，B 定位在 146，C 定位在 300，现在我们可以为每个父节点设置边界值，例如 Pa 的边界可以是 0 和 100，Pb 的是 100 和 280，最后 Pc 的是 280 和 360。对于更高层级的其余节点，则适用经验法则。

为了确定节点 P 的右侧和左侧障碍，我们将检查 P 的每个子节点的角度，以找到最大值和最小值。P 的左侧障碍必须小于最小值，P 的右侧障碍必须大于最大值。

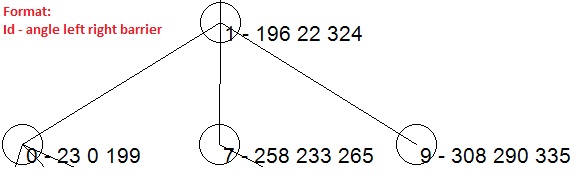
父节点 ID 为 1 的节点有 3 个子节点，最小角度为 23，最大角度为 308，因此 P 的左侧障碍设置为 22，右侧障碍为 324。节点的角度必须落在其右侧和左侧障碍之间，在上面的例子中选择了 196。

扩展树

在向上遍历（从叶子到根）时，我们可能会遇到某个级别上没有子节点的节点。这些节点被认为是死胡同，在这种情况下，由于缺少障碍值，我们将无法确定节点的位置。显然，我们将无法继续向上设置其父障碍。

为了解决这个问题，我们将树扩展为一棵满树：级别小于树高度的每个叶子节点都将被扩展，方法是添加额外的节点，直到它达到树的高度。每个添加的节点都将被标记一个特殊的 ID，以便我们以后能够发现并删除这些额外的节点。

树扩展后，我们可以开始计算，而无需担心遇到死胡同节点。

当我们完成确定每个节点的位置及其左右障碍位置后，我们需要将树收缩回其原始结构。我们通过截断特殊标记的节点来做到这一点。

绘图

我们快完成了。实际绘制迷宫此时相当容易。

我们首先绘制完整的圆，每个圆代表树的一个级别。接下来，我们在圆上绘制弧线，创建可供通行的门，并根据之前计算的角度在环内添加障碍。请注意，我们不需要绘制左右两个障碍。一个就足够了，因为一个节点的障碍也是另一个节点的结束障碍。

总结

1. 创建一棵树来表示您的迷宫。
2. 扩展树（这就是我们将如何处理死胡同）。
3. 运行实际计算，这将确定门和障碍的角度。
4. 将树收缩回其原始结构。
5. 根据存储在树节点中的信息进行绘制。

限制

由于算法的性质，生成的迷宫存在一些限制。例如：两个门永远不会通往同一个死胡同。

解决迷宫的路径永远不会包含玩家回溯的移动，即从内圈到外圈的移动。解路径中的所有移动都将是从圆 i 到圆 i+1。

利用

使用树结构存储关于迷宫/地图的信息可以扩展到跟踪世界中的玩家。我们可以向世界触发事件，使其能够根据需要采取行动。例如，当我们的玩家进入级别“i”的任何节点时，创建四只怪物攻击玩家，或者在玩家解决当前迷宫时重新生成更大的地图。

代码

尽管存在实现图/树数据结构并提供处理它们的（例如 BFS）基本算法的开源库，但我决定编写自己的实现。我的主要原因之一是需要额外的属性来描述树节点。此外，我还添加了一些我缺失的方法，但大多数情况下只是为了好玩。

我知道代码并非完美（并且总有改进的空间），但我认为我的工作处于一个不错的状态。我试图保持代码清晰并带有注释，因此应该很容易理解其流程，尤其是在您阅读了以上内容之后。

未来发展

我目前缺少一种方便的创建图的方法，所以目前代码接受两个输入：深度和扩展，它们用于创建一个节点数等于给定深度的连接图，然后使用扩展值对图进行扩展。

另一个想法是将代码导入网络；创建有趣的迷宫在线解决。

我希望您发现我创建圆形迷宫的方法和我一样有趣。

如有任何问题或评论，请随时与我联系。