图像的仿射变换

仅下载类库（源代码）- 43.8 KB

下载 Windows Mobile 的示例应用程序（源代码）- 97.79 KB  

介绍 

这是我的第一篇 CodeProject 文章，希望您喜欢。进入正题

不幸的是，与 .NET framework 相比，CF 不支持在图像上进行此类操作。   

因此，这个类库实现了图像的仿射变换，例如平移、旋转、缩放、倾斜。算法效率不高，但是很简单。此代码不应用于实时转换，在这种情况下，您需要更高效的东西，一些将 GPU 应用于工作的东西，而不仅仅是可怜的、孤独的 CPU ;>（例如 DirectX API）

算法 

Transforms.ImageTransform(Bitmap dst, Bitmap src, Matrix matTrans, Interpolate sampler)

- 使用定义的插值方法，使用变换矩阵将源图像像素放置到目标图像上。怎么做？

首先，我们需要找到定义的反向变换。为什么？ 

如果您使用定义的矩阵转换源位图的像素并将它们放在目标位图上，则输出图像可能存在“孔洞”。想象一下最简单的 2 倍缩放变换

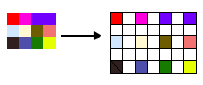
解决该问题的方法是沿相反方向转换。只需遍历所有目标位图的像素，使用逆矩阵转换它们的坐标，以了解像素应该去源位图的哪个位置，另一方面，我们知道源像素应该去目标位图的哪个位置。现在我们必须使用某种插值方法用源像素的颜色填充目标像素。 如果转换后的像素没有去源位图，则目标像素可以保持不变或填充定义的背景颜色。

如何处理源像素的浮点坐标？（插值问题）。

我实现了两种方法：  

• 最近邻插值 - 我们只是将坐标四舍五入到最接近的整数
  

         unsafe
         public static void NearestNeigbour(Pixel* dstPixel, Pixel* src, Vector2 vec, int srcStrideInPixels)
          {
              int tx, ty;
              tx = Convert.ToInt32(vec.x); // Note: Convert.ToInt32 rounds float numbers!
              ty = Convert.ToInt32(vec.y); // Note: Convert.ToInt32 rounds float numbers!
              *dstPixel= src[ty * srcStrideInPixels + tx];
          } 

       

• 双线性插值 - 我们将具有整数坐标的 4 个相邻像素的颜色相加（在浮点坐标上使用 floor、ceiling 操作），并使用以下方式计算的适当权重

（1.0f - 变换像素和相邻像素之间的 X 维度距离）*（1.0f - Y 维度距离）            

如果您仔细查看下图...

假设转换后的像素 P 具有坐标 (4.25f, 11.3f)，则像素 

P0 的坐标为 (4, 11)，其权重为 (1.0f -0.25f) * (1.0f - 0.3f)
P1 的坐标为 (5, 11)，其权重为 (1.0f -0.75f) * (1.0f - 0.3f)
P2 的坐标为 (4, 12)，其权重为 (1.0f -0.25f) * (1.0f - 0.7f)
P3 的坐标为 (5, 12)，其权重为 (1.0f -0.75f) * (1.0f - 0.7f)  

显然，相邻像素越接近变换后的像素，它在最终颜色中就越重要。 

        unsafe
        public static void BilinearInterpolation(Pixel* dstPixel, Pixel* src, Vector2 vec, int srcStrideInPixels)
        {
            Pixel result;
            int tx, ty;
            float f1, f2;
            tx = (int)vec.x; // Note: this is just a truncation of float numbers
            ty = (int)vec.y; // Note: this is just a truncation of float numbers
            f1 = vec.x - (float)tx;
            f2 = vec.y - (float)ty;
            src = src + ty * srcStrideInPixels + tx;
            Pixel upperLeft = *src;
            Pixel upperRight = src[1];
            Pixel bottomLeft = src[srcStrideInPixels];
            Pixel bottomRight = src[srcStrideInPixels + 1];
            result.A = 0;
            result.R = (Byte)((float)upperLeft.R * (1.0f - f1) * (1.0f - f2) + (float)upperRight.R * f1 * (1.0f - f2) +
                       (float)bottomLeft.R * (1.0f - f1) * f2 + (float)bottomRight.R * f1 * f2);
            result.G = (Byte)((float)upperLeft.G * (1.0f - f1) * (1.0f - f2) + (float)upperRight.G * f1 * (1.0f - f2) +
                       (float)bottomLeft.G * (1.0f - f1) * f2 + (float)bottomRight.G * f1 * f2);
            result.B = (Byte)((float)upperLeft.B * (1.0f - f1) * (1.0f - f2) + (float)upperRight.B * f1 * (1.0f - f2) +
                       (float)bottomLeft.B * (1.0f - f1) * f2 + (float)bottomRight.B * f1 * f2);
            *dstPixel = result;
        } 
  

效率

正如您所看到的，算法的效率取决于目标图像的大小以及您选择的插值方法。

有什么改进吗？

 所有数学运算都可以仅用整数运算代替。 如您所知，对整数进行运算比对浮点数进行运算快得多。 但是我们失去了数学运算的精度。 要获得整数的精度，只需乘以某个大数（最好是 2 的幂并进行位移运算），然后进行所需的运算，最后除以相同的数字（建议使用位移运算）。

 位图是像素的有序集合。 使用该事实，您可以创建增量算法。

使用代码 

            using ImageTransforms; 

            Bitmap buffer = new Bitmap(128,128);
            Bitmap srcBuffer = new Bitmap(bmpArrows); //load image for transformations
            Matrix matRot = new Matrix();
            Matrix matTrans1 = new Matrix();
            Matrix matTrans0 = new Matrix();
            matTrans0.Translation(-(float)(srcBuffer.Width) / 2.0f, -(float)(srcBuffer.Height) / 2.0f);
            matRot.Rotation(angle);
            matTrans1.Translation((float)(buffer.Width) / 2.0f, (float)(buffer.Height) / 2.0f);
            unsafe
            {
                Transforms.ImageTransform(buffer, srcBuffer, matTrans1 * (matRot * matTrans0), ImageTransforms.Transforms.NearestNeigbour);
            }
            //now buffer contains our transformed image