研究 Myers 的 diff 算法：第 2 部分，共 2 部分

Nicholas Butler

4.93/5 (11投票s)

2009 年 9 月 11 日

CPOL

5分钟阅读

34269

896

线性空间精炼。

引言

本文是对 Eugene W. Myers 在其论文《O(ND) 差分算法及其变种》中描述的线性空间改进的探讨。该论文于 1986 年 11 月发表在《Algorithmica》期刊上。PDF 版本可在此处获取[^]。

这是关于 Myers 差分算法的系列文章的第二部分，需要理解第一部分中描述的基本贪婪算法，第一部分也发布在 The Code Project 上，可在此处[^] 找到。

下载提供的应用程序是一个学习辅助工具。它以图形方式展示了算法的各个阶段。我建议您在阅读本文时使用它来帮助理解算法。本文中的图表是该应用程序的截图。

反向算法

基本算法也可以反向工作，即从 (N, M) 工作到 (0, 0)。唯一的区别在于移动从删除/插入/匹配开始，而不是结束于它们。这是示例的解决方案，但反向工作。

图 1：反向解决方案

从图中可以看出，该解决方案与向前工作生成的解决方案不同，但具有相同的 LCS 和 SES 长度。这是完全正确的，因为通常可以存在许多等效的解决方案，算法只是选择它找到的第一个。

增量：由于序列 A 和 B 的长度可能不同，正向和反向算法的 k 行可能不同。将此差异隔离为一个变量 delta = N - M 会很有用。在示例中，N = 7 且 M = 6，则 delta = 1。这是从正向 k 行到反向 k 行的偏移量。可以说，正向路径围绕 k = 0 对称，反向路径围绕 k = delta 对称。

中间蛇

重叠

您可以同时运行正向和反向算法，针对 D 的连续值。在某个 D 值下，两条蛇会在某条 k 线上重叠。论文证明其中一条蛇是解决方案的一部分。由于它会出现在中间的某个位置，因此称为中间蛇。

示例的中间蛇在此图的粉红色部分显示

图 2：中间蛇

这很有用，因为它将问题分成两部分，然后可以单独递归地解决。

这是线性的空间复杂度，因为只需要存储最后的 V 个向量，即 O(D)。时间复杂度方面，这个线性算法仍然是 O((N+M)D)。

中间蛇必须以 D 为前向和后向算法 D 的一半来找到，这也很有帮助。这意味着随着 D 的增加，所需时间接近基本算法的一半。

下面是我们到目前为止的伪代码

for d = 0 to ( N + M + 1 ) / 2
{
  for k = -d to d step 2
  {
    calculate the furthest reaching forward and reverse paths
    if there is an overlap, we have a middle snake
  }
}

奇偶增量

每个差异——水平删除或垂直插入——都是从一条 k 线移动到其相邻线。由于 delta 是正向和反向算法中心之间的差异，因此我们知道需要检查哪些 d 值来寻找中间蛇。

对于奇数 delta，我们必须寻找前向路径与差异 d 的重叠，以及后向路径与差异 d-1 的重叠。

此图显示，对于 delta = 3，当正向 d 为 2 且后向 d 为 1 时发生重叠

图 3：奇数增量

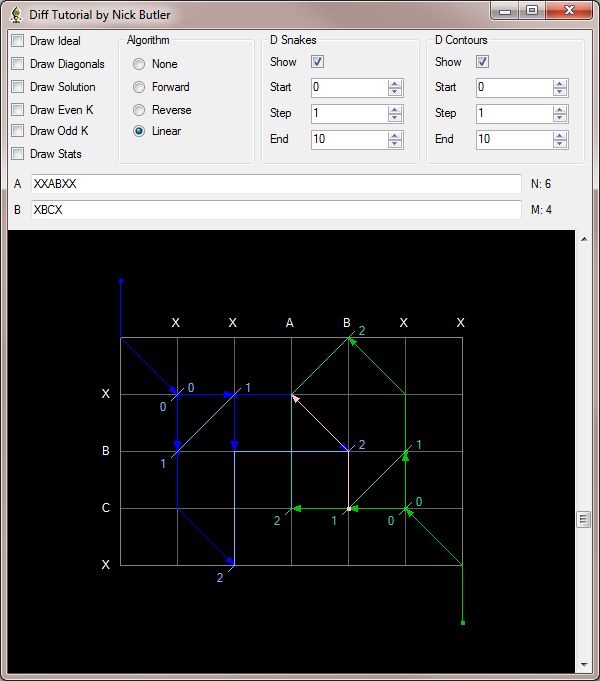
同样，对于偶数 delta，重叠将发生在正向和反向路径具有相同数量的差异时。

下一个图显示，对于 delta = 2，当正向和反向 ds 都为 2 时发生重叠

图 4：偶数增量

算法

因此，这是寻找中间蛇的完整伪代码

delta = N - M
for d = 0 to ( N + M + 1 ) / 2
{
  for k = -d to d step 2
  {
    calculate the furthest reaching forward path on line k
    if delta is odd and ( k >= delta - ( d - 1 ) and k <= delta + ( d - 1 ) )
      if overlap with reverse[ d - 1 ] on line k
        => found middle snake and SES of length 2D - 1
  }
  
  for k = -d to d step 2
  {
    calculate the furthest reaching reverse path on line k
    if delta is even and ( k >= -d - delta and k <= d - delta )
      if overlap with forward[ d ] on line k
        => found middle snake and SES of length 2D
  }
}

注意： k 的边界检查只是为了消除不可能的重叠。

递归解决方案

算法

我们需要将中间蛇算法包装在一个递归方法中。基本上，我们需要找到一个中间蛇，然后分别解决左上角和右下角的剩余矩形。有几个边缘情况我将在稍后解释。我已经添加了 SES 的解决方案，因为论文将此留作“练习”，只找到 LCS。

Compare( A, N, B, M )
{
  if ( M == 0 && N > 0 ) add N deletions to SES
  if ( N == 0 && M > 0 ) add M insertions to SES
  if ( N == 0 || M == 0 ) return
  
  calculate middle snake
  
  suppose it is from ( x, y ) to ( u, v ) with total differences D
  
  if ( D > 1 )
  {
    Compare( A[ 1 .. x ], x, B[ 1 .. y ], y ) // top left
    
    Add middle snake to results
    
    Compare( A[ u + 1 .. N ], N - u, B[ v + 1 .. M ], M - v ) // bottom right
  }
  else if ( D == 1 ) // must be forward snake
  {
    Add d = 0 diagonal to results
    Add middle snake to results
  }
  else if ( D == 0 ) // must be reverse snake
  {
    Add middle snake to results
  }
}

我希望一般情况相当清楚。现在我将探讨两个边缘情况。

边缘情况：D == 0

如果中间蛇算法找到 D = 0 的解决方案，则这两个序列是相同的。这意味着 delta 为零，这是偶数。因此，中间蛇是仅由匹配（对角线）组成的反向蛇。所以我们只需要将这条蛇添加到结果中。

下图显示了此边缘情况的一般形式

图 5：D = 0 的解决方案

边缘情况：D == 1

如果中间蛇算法找到 D = 1 的解决方案，则只有一次插入或删除。这意味着 delta 为 1 或 -1，它们是奇数，因此中间蛇是正向蛇。

我们可以通过计算 d = 0 的对角线，并将其与中间蛇一起添加到结果中来完成此案例的解决方案。