65.9K
CodeProject 正在变化。 阅读更多。
Home

您的数字喷泉

Omar Gameel Salem
starIconstarIconstarIconstarIcon
emptyStarIcon
starIcon

4.97/5 (45投票s)

2012 年 7 月 20 日

CPOL

4分钟阅读

viewsIcon

96081

downloadIcon

215

在有损连接上可靠地传输大量数据， 而无需担心数据包丢失

下载源代码 

介绍 

在C#中实现Luby变换代码，并提供WPF和WCF的演示应用程序。

问题 

传统的文件传输机制如下： 

  1.         文件被分成等长的数据包。 
  2.         发送方逐个发送数据包。
  3.         接收方确认已接收到的数据包以及丢失的数据包。
  4.         发送方重新发送丢失的数据包。

       
现在考虑一个场景，服务器需要将数据分发给多个接收方，内容可以是操作系统更新或媒体文件，任何内容。

使用传统方法，服务器不仅需要与客户端保持双向通信，还需要维护一个列表，记录哪个客户端接收了哪些数据包，以便重新传输丢失的数据包。
       


想象您是NASA火星探测任务的一员，尽管计算能力非常强大，但与地球的连接非常不稳定，您发送的许多数据包都会丢失，而您无法提供任何关于需要重新传输哪些数据包的反馈。

解决方案

在数字喷泉中，接收到哪些数据包和丢失了哪些数据包并不重要，接收到的数据包的顺序也无关紧要。

服务器将数据转换为无限数量的编码块，然后客户端只要获得足够数量的块，就可以重新组合数据，无论接收到哪些块，丢失了哪些块。
        
这就是为什么它被称为喷泉，您不必关心从喷泉中得到哪一滴水，只要您得到足够的水滴来装满您的瓶子即可。
 

工作原理

编码

解码

 

示例  

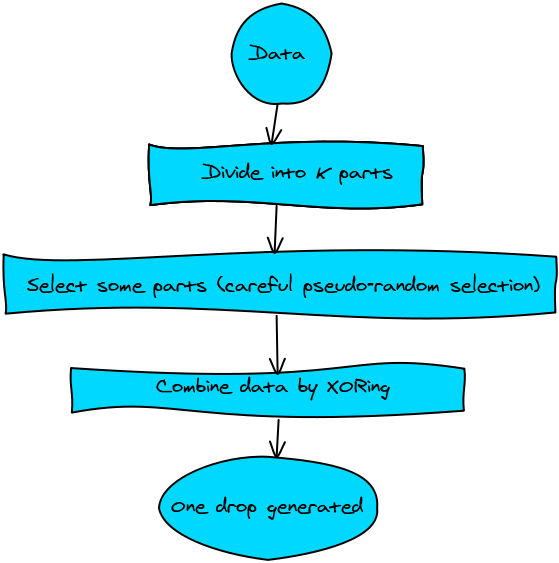
Data

分成 k = 6 个部分

 

一个数据滴是通过 XOR 部分 1、2 和 3 生成的

 

另一个数据滴是通过 XOR 部分 1、5 和 6 生成的

数据滴生成可以重复进行，直到需要为止

 

解码

这相当于解决一个有 k 个未知数（数据部分）的方程组。每个数据滴都是该系统的一个方程。

很好，那么，如果我们知道文件被分成 K 个块，那么我们就需要 K 个数据滴（*方程*），对吗？

不对！只有 k 个数据滴，在最有利的情况下，解码成功的几率只有 30%。

为了提高解码的概率，有必要收集超过 k 个数据滴。多余数据滴的数量是**开销**；开销越大，解码的概率就越高。

请注意，开销与 k 无关：对于任何 k，为了获得 10-6 的失败概率，需要 20 个多余的数据滴（*那么当 K 很大时效果更好*）。 

代码架构 



文件夹 **Algorithm** 是实现逻辑所在，**MathHelper** 用于使用高斯-约旦消元法解线性方程组，**Server** 是一个自托管的 WCF 服务，公开算法，**Client** 是 WPF 应用程序，它将数据滴接收到杯子中，然后将其解码为原始文件。

 

代码解释

 

LubyTransform.Encode（**Server** 部分）

首先进行初始化，我们将数据文件分成块。
注意变量 degree，它决定了要组合的最大块数。
这里 degree 等于生成块数除以 2。

 

   

 public class Encode : IEncode
    {
        #region Member Variables

        readonly IList<byte[]> blocks;
        readonly int degree;
        readonly Random rand;
        readonly int fileSize;
        const int chunkSize = 2;

        #endregion

        #region Constructor

        public Encode(byte[] file)
        {
            rand = new Random();
            fileSize = file.Length;
            blocks = CreateBlocks(file);
            degree = blocks.Count() / 2;
            degree += 2;
        }

        #endregion

 


然后我们有了 Encode() 方法本身

 

 

Drop IEncode.Encode()
        {
            int[] selectedParts = GetSelectedParts();
            byte[] data;

            if (selectedParts.Count() > 1)
            {
                data = CreateDropData(selectedParts, blocks, chunkSize);
            }
            else
            {
                data = blocks[selectedParts[0]];
            }

            return new Drop { SelectedParts = selectedParts, Data = data };
        }

 

很简单，我们随机选择一些块（degree *是我们选择的最大块数*）并将它们组合起来，生成数据滴数据。 

         private byte[] CreateDropData(IList<int> selectedParts, IList<byte[]> blocks, int chunkSize)
        {
            var data = new byte[chunkSize];

            for (int i = 0; i < chunkSize; i++)
            {
                data[i] = XOROperation(i, selectedParts, blocks);
            }

            return data;
        }

        private byte XOROperation(int idx, IList<int> selectedParts, IList<byte[]> blocks)
        {
            var selectedBlock = blocks[selectedParts[0]];
            byte result = selectedBlock[idx];

            for (int i = 1; i < selectedParts.Count; i++)
            {
                result ^= blocks[selectedParts[i]][idx];
            }

            return result;
        }

组合是通过将部分 **XOR** 在一起完成的。请注意，每次请求数据滴时选择的块数是不同的。每个数据滴包含组合生成的数据，以及一个包含组合块列表的列表。 

    public class Drop
    {
        public IList<int> SelectedParts { get; set; }
        public byte[] Data { get; set; }
    }

LubyTransform.Decode（**Client** 部分，整合所有内容）

我们做的第一件事是收集数据滴，我们需要 K+开销个数据滴。

private string ReceiveMessage()
        {
            var blocksCount = encodeServiceClient.GetNumberOfBlocks();
            var fileSize = encodeServiceClient.GetFileSize();
            var chunkSize = encodeServiceClient.GetChunkSize();
            IList<Drop> goblet = new List<Drop>();

            for (int i = 0; i < blocksCount + overHead; i++)
            {
                var drop = encodeServiceClient.Encode();
                goblet.Add(drop);
            }

            var fileData = _decoder.Decode(goblet, blocksCount, chunkSize, fileSize);
            return Encoding.ASCII.GetString(fileData);
        }

从这些数据滴中，我们构建一个**增广矩阵**，用高斯-约旦消元法来求解。

        byte[] IDecode.Decode(IList<Drop> goblet, int blocksCount, int chunkSize, int fileSize)
        {
            var matrix = BuildMatrix(goblet, blocksCount, chunkSize);
            matrixSolver.Solve(matrix);
            int columnsCount = matrix.GetLength(1);
            byte[] result = new byte[fileSize];

            for (int i = 0; i < result.Length; i++)
            {
                result[i] = (byte)matrix[i, columnsCount - 1];
            }

            return result;
        }

就是这样，文件被重建了。

如何使用该应用程序

  1. 以管理员权限启动 Visual Studio。
  2. 将 **Server.Host** 设置为启动项目，确保它已启动并运行。
  3. 启动 **Client.Receiver** 项目的新实例（右键单击项目-->Debug-->start new instance）。
  4. 按 **Start Receiving** 按钮，您应该会收到存储在服务器上的消息。

关注点

  • 块的 **XOR** 操作是一个非常耗时的过程，请注意 CreateDropData() 函数，每次请求一个数据滴时，我们都会循环 ChunkSize 次。在这个特定的演示中，我将 ChunkSize 设置为 2，但在实际应用中，它将不少于 4 Kb，甚至可能是 16 Kb，这将花费难以想象的时间！ 
  • 高斯-约旦算法的执行时间为 O(mnm)，大致为 O(n3)。 

参考资料  

历史

  • 2012 年 8 月 24 日 采纳了 Paulo Zemek 的建议，使用 IList 而不是 IEnumerable。
  • 2012 年 7 月 21 日  初始发布
© . All rights reserved.